Question and Answers Forum

AllQuestion and Answers: Page 529

Question Number 167021 Answers: 0 Comments: 0

how can it solve this ? (1)sin360 (2)tan345 (3)cos170 (4)sec150 (5)cot150

$${how}\:{can}\:{it}\:{solve}\:{this}\:? \\ $$$$ \\ $$$$\left(\mathrm{1}\right){sin}\mathrm{360} \\ $$$$\left(\mathrm{2}\right){tan}\mathrm{345} \\ $$$$\left(\mathrm{3}\right){cos}\mathrm{170} \\ $$$$\left(\mathrm{4}\right){sec}\mathrm{150} \\ $$$$\left(\mathrm{5}\right){cot}\mathrm{150} \\ $$

Question Number 167013 Answers: 1 Comments: 0

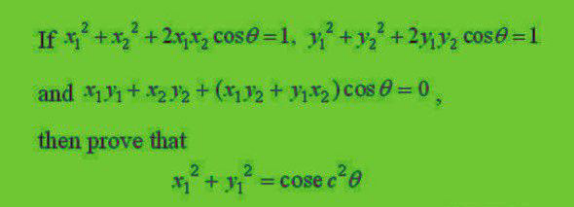
Question Number 167011 Answers: 2 Comments: 0

Question Number 167010 Answers: 1 Comments: 0

Question Number 167009 Answers: 1 Comments: 0

Question Number 167008 Answers: 1 Comments: 0

Question Number 167007 Answers: 1 Comments: 0

Question Number 167006 Answers: 1 Comments: 0

∫ ((3x^3 )/((x−1)^3 )) dx=?

$$\:\:\:\:\:\:\:\int\:\frac{\mathrm{3x}^{\mathrm{3}} }{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} }\:\mathrm{dx}=? \\ $$

Question Number 167002 Answers: 0 Comments: 0

calculate :: lim_(t→∞) 8∫_0 ^(π/2) e^x ∙sin (tx)∙sin (2tx)∙cos (3tx)∙cos (4tx)dx=?

$$\mathrm{calculate}\:\:::\:\:\underset{\mathrm{t}\rightarrow\infty} {\mathrm{lim}8}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{e}^{\mathrm{x}} \centerdot\mathrm{sin}\:\left(\mathrm{tx}\right)\centerdot\mathrm{sin}\:\left(\mathrm{2tx}\right)\centerdot\mathrm{cos}\:\left(\mathrm{3tx}\right)\centerdot\mathrm{cos}\:\left(\mathrm{4tx}\right)\mathrm{dx}=? \\ $$

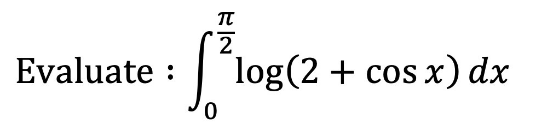
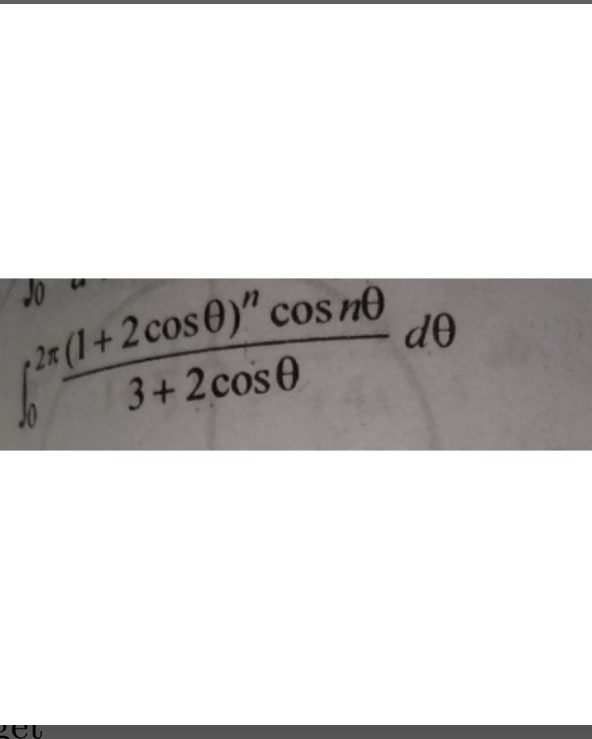
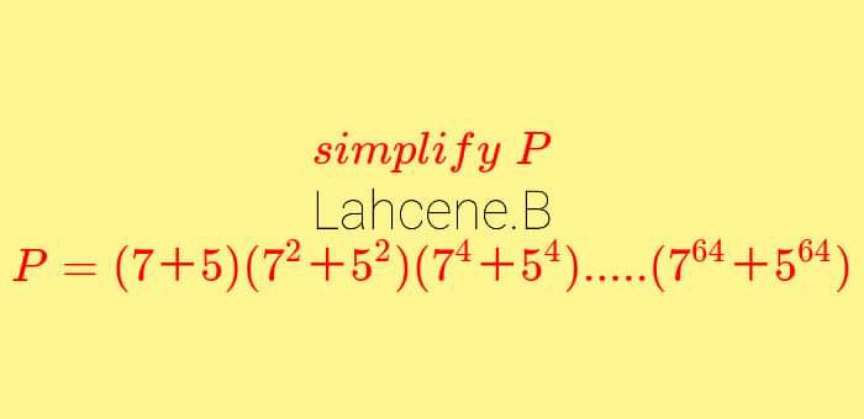
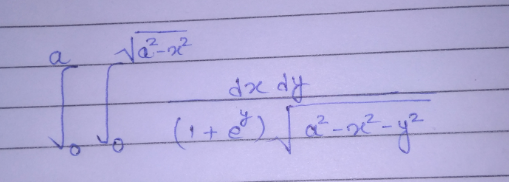
Question Number 167004 Answers: 0 Comments: 0

calculate :: lim_(x→(√π)) ∫_(√π) ^x (((x^2 +(√π)t)e^t^2 )/((x−(√π))(x^2 +π)t^2 lnt))dt=?

$$\mathrm{calculate}\:::\:\:\underset{\mathrm{x}\rightarrow\sqrt{\pi}} {\mathrm{lim}}\int_{\sqrt{\pi}} ^{\mathrm{x}} \frac{\left(\mathrm{x}^{\mathrm{2}} +\sqrt{\pi}\mathrm{t}\right)\mathrm{e}^{\mathrm{t}^{\mathrm{2}} } }{\left(\mathrm{x}−\sqrt{\pi}\right)\left(\mathrm{x}^{\mathrm{2}} +\pi\right)\mathrm{t}^{\mathrm{2}} \mathrm{lnt}}\mathrm{dt}=? \\ $$

Question Number 167003 Answers: 1 Comments: 0

Σ_(n=2) ^(n=∞) ((3/4))^n cos (180°n)= ?

$$\:\:\:\:\:\underset{\mathrm{n}=\mathrm{2}} {\overset{\mathrm{n}=\infty} {\sum}}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{n}} \mathrm{cos}\:\left(\mathrm{180}°\mathrm{n}\right)=\:? \\ $$

Question Number 166994 Answers: 2 Comments: 0

1+1≠??

$$\mathrm{1}+\mathrm{1}\neq?? \\ $$

Question Number 166982 Answers: 1 Comments: 3

hi! help me! lim_(x→∞) ∫_0 ^∞ e^2 c(√x)∫_0 ^∞ =?

$$\mathrm{hi}! \\ $$$$\mathrm{help}\:\mathrm{me}! \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{\mathrm{2}} \mathrm{c}\sqrt{{x}}\int_{\mathrm{0}} ^{\infty} =? \\ $$

Question Number 167098 Answers: 3 Comments: 0

find the maximum of f(x)=sin x+cos x+sin x cos x

$${find}\:{the}\:{maximum}\:{of} \\ $$$${f}\left({x}\right)=\mathrm{sin}\:{x}+\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\:\mathrm{cos}\:{x} \\ $$

Question Number 166975 Answers: 3 Comments: 3

hi ! help me ! lim_(x→−∞) (e^(1/(x+(√(x^2 +1)))) /x) = ???

$$\mathrm{hi}\:!\: \\ $$$$\mathrm{help}\:\mathrm{me}\:! \\ $$$$\underset{\boldsymbol{{x}}\rightarrow−\infty} {\boldsymbol{{lim}}}\:\frac{\boldsymbol{{e}}^{\frac{\mathrm{1}}{\boldsymbol{{x}}+\sqrt{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}}} }{\boldsymbol{{x}}}\:=\:??? \\ $$

Question Number 166959 Answers: 1 Comments: 0

γ=∫ ((e^x (sin x+1))/(cos x+1)) dx =?

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\gamma=\int\:\frac{\mathrm{e}^{\mathrm{x}} \left(\mathrm{sin}\:\mathrm{x}+\mathrm{1}\right)}{\mathrm{cos}\:\mathrm{x}+\mathrm{1}}\:\mathrm{dx}\:=? \\ $$

Question Number 166958 Answers: 3 Comments: 1

If polynomial x^3 −9x^2 +11x−1=0 have the roots are a,b an c . Given Δ = (√a) + (√b) + (√c) then Δ^4 −18Δ^2 −8Δ =?

$$\:\:\mathrm{If}\:\mathrm{polynomial}\:\mathrm{x}^{\mathrm{3}} −\mathrm{9x}^{\mathrm{2}} +\mathrm{11x}−\mathrm{1}=\mathrm{0}\: \\ $$$$\:\mathrm{have}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{are}\:\mathrm{a},\mathrm{b}\:\mathrm{an}\:\mathrm{c}\:. \\ $$$$\:\mathrm{Given}\:\Delta\:=\:\sqrt{\mathrm{a}}\:+\:\sqrt{\mathrm{b}}\:+\:\sqrt{\mathrm{c}}\:\mathrm{then}\: \\ $$$$\:\:\Delta^{\mathrm{4}} −\mathrm{18}\Delta^{\mathrm{2}} −\mathrm{8}\Delta\:=? \\ $$$$ \\ $$

Question Number 166956 Answers: 1 Comments: 0

calculate ∫_0 ^( ∞) (((√x) arctan(x))/(1+x^( 2) ))dx =?

$$ \\ $$$$\:\:\:\:{calculate} \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{\sqrt{{x}}\:{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\:\mathrm{2}} }{dx}\:=? \\ $$

Question Number 166954 Answers: 1 Comments: 0

Given x^3 −3x^2 (√2) +6x−2(√2)−8=0 then x^5 −41x^2 +2022 =?

$$\:\mathrm{Given}\:\mathrm{x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} \sqrt{\mathrm{2}}\:+\mathrm{6x}−\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{8}=\mathrm{0} \\ $$$$\:\mathrm{then}\:\mathrm{x}^{\mathrm{5}} −\mathrm{41x}^{\mathrm{2}} +\mathrm{2022}\:=? \\ $$

Question Number 166950 Answers: 0 Comments: 3

Question Number 166943 Answers: 1 Comments: 2

Question Number 166940 Answers: 1 Comments: 0

Question Number 166939 Answers: 1 Comments: 0

Question Number 166929 Answers: 1 Comments: 0

A particle of mass 0.25kg vibrates with a period of 2secs. If its greatest displacement is 0.4m. What is its maximum kinetic energy.

$$\:{A}\:{particle}\:{of}\:{mass}\:\mathrm{0}.\mathrm{25}{kg}\:{vibrates} \\ $$$$\:{with}\:{a}\:{period}\:{of}\:\mathrm{2}{secs}.\:{If}\:{its}\: \\ $$$$\:{greatest}\:{displacement}\:{is}\:\mathrm{0}.\mathrm{4}{m}.\:{What} \\ $$$$\:{is}\:{its}\:{maximum}\:{kinetic}\:{energy}. \\ $$

Question Number 166928 Answers: 1 Comments: 0

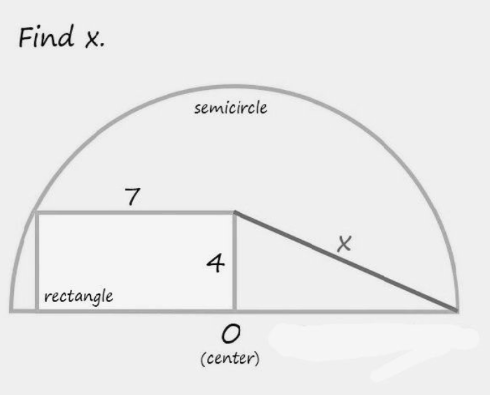
Question Number 166926 Answers: 3 Comments: 0

lim_(n→∞) (5^n /(n!))=?

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{5}^{{n}} }{{n}!}=? \\ $$

Pg 524 Pg 525 Pg 526 Pg 527 Pg 528 Pg 529 Pg 530 Pg 531 Pg 532 Pg 533

Contact: info@tinkutara.com