
AllQuestion and Answers: Page 525
Question Number 167782 Answers: 1 Comments: 0
Question Number 167808 Answers: 1 Comments: 1

Question Number 167777 Answers: 1 Comments: 0
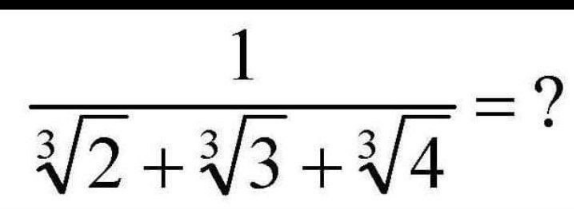
Question Number 167776 Answers: 2 Comments: 0

Question Number 167775 Answers: 1 Comments: 1
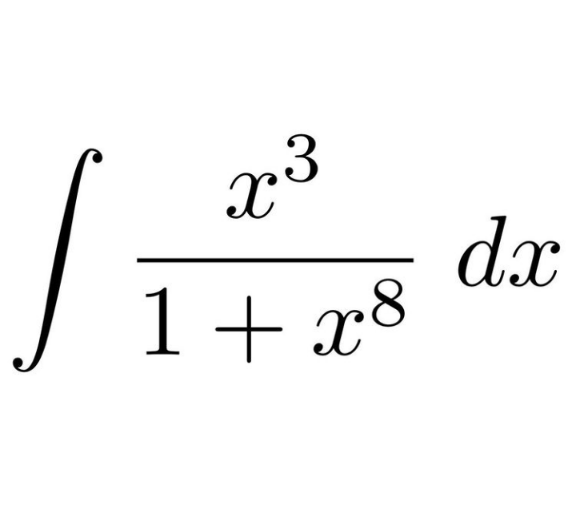
Question Number 167765 Answers: 0 Comments: 0
$$ \\ $$show that two permutations are conjugate if their matrices are similar
Question Number 167773 Answers: 2 Comments: 0
$${Calculate} \\ $$$$\int\frac{{x}\mathrm{tan}\:{x}}{\mathrm{cos}\:^{\mathrm{4}} {x}}{dx} \\ $$
Question Number 167757 Answers: 1 Comments: 1
$${Calculate} \\ $$$$\int\mathrm{sec}\:^{\mathrm{2}} {x}\mathrm{sec}\:{xdx} \\ $$
Question Number 167746 Answers: 1 Comments: 1
Question Number 167740 Answers: 0 Comments: 0
Question Number 167739 Answers: 4 Comments: 2

Question Number 167738 Answers: 2 Comments: 0
Question Number 167737 Answers: 1 Comments: 0
Question Number 167730 Answers: 1 Comments: 2

Question Number 167772 Answers: 1 Comments: 2
$${x}+\sqrt{{x}}=\mathrm{5} \\ $$$${x}+\frac{\mathrm{5}}{\:\sqrt{{x}}}=? \\ $$
Question Number 167750 Answers: 1 Comments: 0
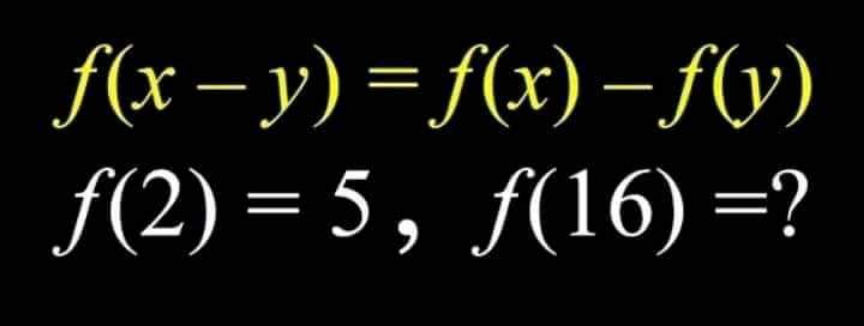
Question Number 167725 Answers: 1 Comments: 4
Question Number 167722 Answers: 1 Comments: 1
Question Number 167718 Answers: 0 Comments: 2
Question Number 167716 Answers: 1 Comments: 0

Question Number 167713 Answers: 1 Comments: 0
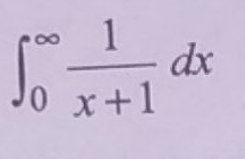
Question Number 167709 Answers: 0 Comments: 0

Question Number 167700 Answers: 1 Comments: 0
Question Number 167699 Answers: 4 Comments: 0

Question Number 167696 Answers: 1 Comments: 0
$${solv}:\:\: \\ $$$${e}^{{x}} +{x}+\mathrm{1}=\mathrm{0} \\ $$
Question Number 167690 Answers: 1 Comments: 0

Pg 520 Pg 521 Pg 522 Pg 523 Pg 524 Pg 525 Pg 526 Pg 527 Pg 528 Pg 529
