Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 521

Question Number 167647 Answers: 2 Comments: 0

Question Number 167626 Answers: 0 Comments: 0

∫_0 ^∞ (e^(−t) /( (√t))) e^(−(1/(4t))) dt

$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} }{\:\sqrt{{t}}}\:{e}^{−\frac{\mathrm{1}}{\mathrm{4}{t}}} \:{dt} \\ $$

Question Number 167624 Answers: 2 Comments: 0

solve Ω =lim_( n→∞) n^( 2) . ln( n . sin((1/n)))=?

$$ \\ $$$$\:\:{solve} \\ $$$$\:\:\Omega\:={lim}_{\:{n}\rightarrow\infty} {n}^{\:\mathrm{2}} .\:{ln}\left(\:{n}\:.\:{sin}\left(\frac{\mathrm{1}}{{n}}\right)\right)=? \\ $$$$ \\ $$

Question Number 167633 Answers: 1 Comments: 6

Question Number 167630 Answers: 0 Comments: 0

Question Number 167617 Answers: 3 Comments: 0

(1)lim_(x→0) [tan((π/4)−x)]^(cotx) =? (2)lim_(x→0) [(1/(sin x))−(1/x)]=?

$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[{tan}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right]^{{cotx}} =? \\ $$$$\left(\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{\mathrm{1}}{\mathrm{sin}\:{x}}−\frac{\mathrm{1}}{{x}}\right]=? \\ $$

Question Number 167616 Answers: 0 Comments: 0

How do i show that A\B⊕C=(A\B)⊕(A\C)

$$\boldsymbol{{How}}\:\boldsymbol{{do}}\:\boldsymbol{{i}}\:\boldsymbol{{show}}\:\boldsymbol{{that}} \\ $$$$\:\boldsymbol{{A}}\backslash\boldsymbol{{B}}\oplus\boldsymbol{{C}}=\left(\boldsymbol{{A}}\backslash\boldsymbol{{B}}\right)\oplus\left(\boldsymbol{{A}}\backslash\boldsymbol{{C}}\right) \\ $$

Question Number 167615 Answers: 0 Comments: 0

lim_(x→1) (((√(3+x)) ((7+x^3 ))^(1/3) −4)/((x−1)^2 )) =?

$$\:\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{3}+\mathrm{x}}\:\sqrt[{\mathrm{3}}]{\mathrm{7}+\mathrm{x}^{\mathrm{3}} }−\mathrm{4}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:=? \\ $$$$ \\ $$

Question Number 167612 Answers: 0 Comments: 1

Question Number 167609 Answers: 1 Comments: 0

Question Number 167601 Answers: 0 Comments: 0

Question Number 167598 Answers: 1 Comments: 0

∫ (x/(5x^4 +x^3 −5x−1)) dx=?

$$\:\:\:\:\:\:\int\:\frac{\mathrm{x}}{\mathrm{5x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{3}} −\mathrm{5x}−\mathrm{1}}\:\mathrm{dx}=? \\ $$

Question Number 167596 Answers: 1 Comments: 0

∫ ((cos 7x−cos 8x)/(1+2cos 5x)) dx =?

$$\:\:\int\:\frac{\mathrm{cos}\:\mathrm{7x}−\mathrm{cos}\:\mathrm{8x}}{\mathrm{1}+\mathrm{2cos}\:\mathrm{5x}}\:\mathrm{dx}\:=? \\ $$

Question Number 167594 Answers: 1 Comments: 0

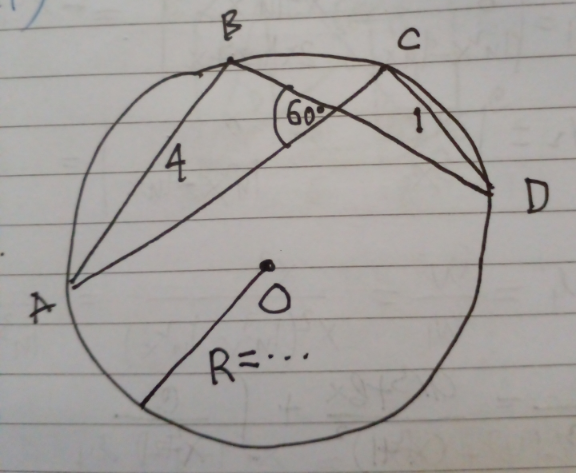
Question Number 167593 Answers: 2 Comments: 0

Question Number 167588 Answers: 1 Comments: 0

1+1=¿

$$\mathrm{1}+\mathrm{1}=¿ \\ $$

Question Number 167586 Answers: 2 Comments: 1

λ=∫ (dx/( (√(1+cos x))+(√(1+sin x)))) =?

$$\:\:\:\:\:\:\:\:\lambda=\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}+\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}}\:=? \\ $$

Question Number 167628 Answers: 0 Comments: 1

Question Number 167627 Answers: 0 Comments: 0

Question Number 167576 Answers: 1 Comments: 1

prove by useing the polar cordinaite ∫_0 ^( (a/2)) ∫_y ^( (√(a^2 −y^2 ))) x dx dy = ((5 a^3 )/(24 ))

$$\boldsymbol{{prove}}\:\boldsymbol{{by}}\:\boldsymbol{{useing}}\:\boldsymbol{{the}}\:\boldsymbol{{polar}}\:\boldsymbol{{cordinaite}}\: \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\:\frac{\boldsymbol{{a}}}{\mathrm{2}}} \:\:\:\int_{\boldsymbol{{y}}} ^{\:\sqrt{\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{y}}^{\mathrm{2}} }} \:\boldsymbol{{x}}\:\boldsymbol{{dx}}\:\boldsymbol{{dy}}\:\:=\:\frac{\mathrm{5}\:\boldsymbol{{a}}^{\mathrm{3}} }{\mathrm{24}\:} \\ $$

Question Number 167567 Answers: 1 Comments: 3

Find the coordinates of the point on the curve y=3x^2 −2x−5, where the tangent is parallel to the line y−5=8x.

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{coordinates}\:\mathrm{of}\:\mathrm{the}\:\mathrm{point}\:\mathrm{on}\:\mathrm{the} \\ $$$$\mathrm{curve}\:\mathrm{y}=\mathrm{3x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{5},\:\mathrm{where}\:\mathrm{the}\:\mathrm{tangent} \\ $$$$\mathrm{is}\:\mathrm{parallel}\:\mathrm{to}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}−\mathrm{5}=\mathrm{8x}. \\ $$

Question Number 167566 Answers: 1 Comments: 0

Question Number 167562 Answers: 1 Comments: 0

∫ (e^(−x) /(1+e^x )) dx=?

$$\:\:\:\:\:\:\:\:\int\:\frac{{e}^{−{x}} }{\mathrm{1}+{e}^{{x}} }\:{dx}=? \\ $$

Question Number 167554 Answers: 3 Comments: 0

∫_0 ^∞ ((3x^2 )/( (√((5x^2 +1)^3 )))) dx

$$\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{3x}^{\mathrm{2}} }{\:\sqrt{\left(\mathrm{5x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }}\:\mathrm{dx} \\ $$$$ \\ $$

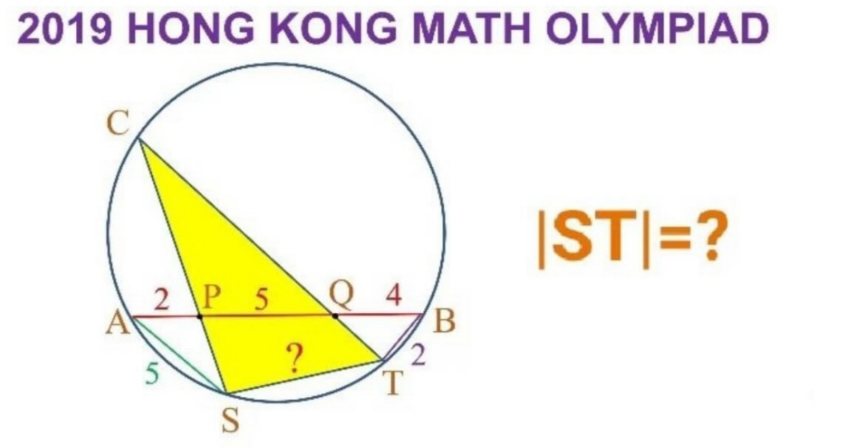
Question Number 167550 Answers: 2 Comments: 0

Question Number 167549 Answers: 0 Comments: 0

Pg 516 Pg 517 Pg 518 Pg 519 Pg 520 Pg 521 Pg 522 Pg 523 Pg 524 Pg 525

Contact: info@tinkutara.com