Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 513

Question Number 167426 Answers: 0 Comments: 1

∫ ((sec^2 x)/(x^2 +1)) dx

$$\int\:\frac{{sec}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$

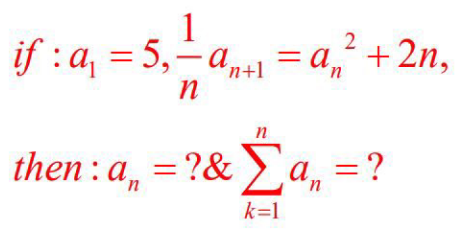
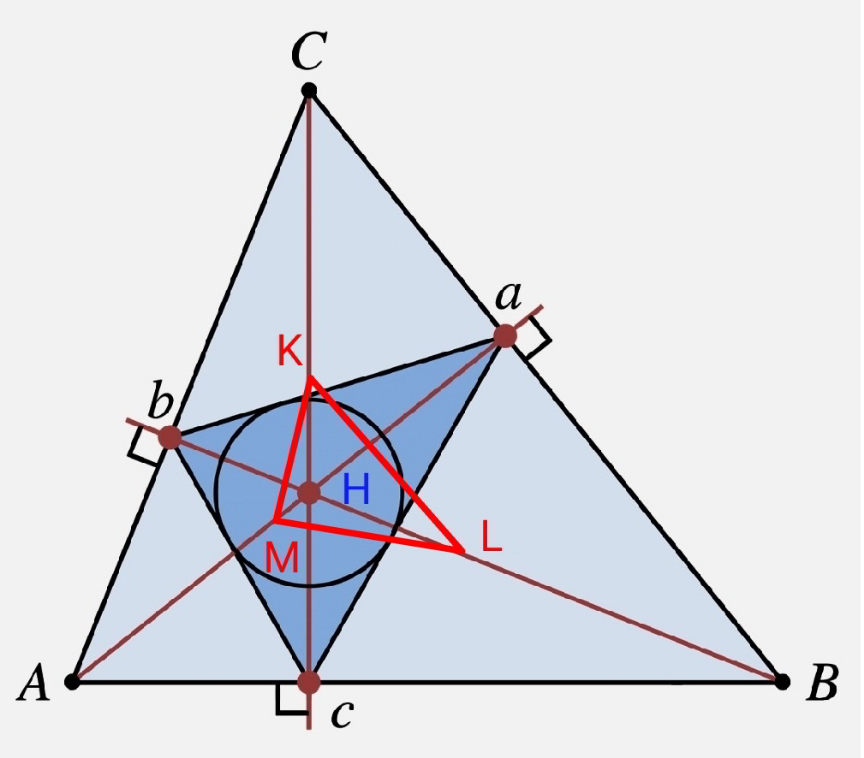
Question Number 167421 Answers: 1 Comments: 0

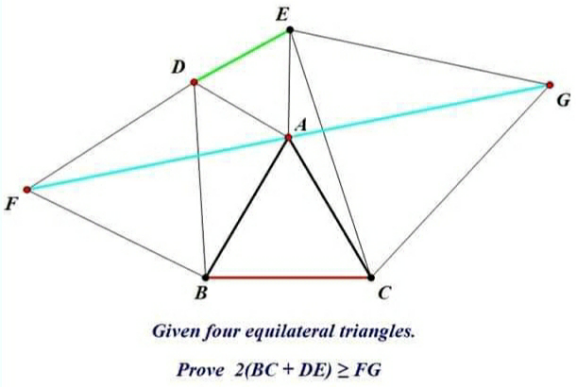
Question Number 167419 Answers: 1 Comments: 1

((1/2))!=? Use Method and Formula!!!!!!!!!

$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)!=? \\ $$$${Use}\:{Method}\:{and}\:{Formula}!!!!!!!!! \\ $$

Question Number 167418 Answers: 0 Comments: 0

x^y =z (z)^(1/y) =x log_x (z)=y

$${x}^{{y}} ={z} \\ $$$$\sqrt[{{y}}]{{z}}={x} \\ $$$$\mathrm{log}_{{x}} \left({z}\right)={y} \\ $$

Question Number 167416 Answers: 0 Comments: 3

∫_( 0) ^( π) ((x.sin (x))/(1+cos^2 (x) ))dx ∫_0 ^( π) (1/(1+cos^3 (x) +sin^3 (x) ))dx ∫_0 ^(π/2) ((x.cos(x)sin(x))/(tan^2 (x)+ cot^2 (x) ))dx ∫_0 ^( 1) tan^(−1) ((√(1−x^2 )))dx

$$\int_{\:\mathrm{0}} ^{\:\pi} \:\frac{{x}.\mathrm{sin}\:\left({x}\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \left({x}\right)\:}{dx} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\:\:\pi} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}^{\mathrm{3}} \left({x}\right)\:+\mathrm{sin}^{\mathrm{3}} \left({x}\right)\:}{dx} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{x}.\mathrm{cos}\left(\mathrm{x}\right)\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{tan}^{\mathrm{2}} \left(\mathrm{x}\right)+\:\mathrm{cot}^{\mathrm{2}} \left(\mathrm{x}\right)\:}\mathrm{dx} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$ \\ $$

Question Number 167445 Answers: 0 Comments: 0

Question Number 167404 Answers: 1 Comments: 0

Question Number 167443 Answers: 1 Comments: 0

Question Number 167402 Answers: 0 Comments: 2

find (d^n /dx^n ) [ ln (cosx) ]

$$\boldsymbol{{find}}\:\frac{\boldsymbol{{d}}^{\boldsymbol{{n}}} }{\boldsymbol{{dx}}^{\boldsymbol{{n}}} }\:\left[\:\boldsymbol{{ln}}\:\left(\boldsymbol{{cosx}}\right)\:\right] \\ $$

Question Number 167400 Answers: 2 Comments: 0

Question Number 167393 Answers: 1 Comments: 0

Question Number 167392 Answers: 2 Comments: 0

f(x)=n! ((df(x)^n )/(d(x)^n ))=?

$${f}\left({x}\right)={n}! \\ $$$$\frac{{df}\left({x}\right)^{{n}} }{{d}\left({x}\right)^{{n}} }=? \\ $$

Question Number 167386 Answers: 0 Comments: 0

show that (A⊕B)′ = A ∩ B

$$\:\boldsymbol{{show}}\:\boldsymbol{{that}}\: \\ $$$$\:\left(\boldsymbol{{A}}\oplus\boldsymbol{{B}}\right)'\:=\:\boldsymbol{{A}}\:\cap\:\boldsymbol{{B}} \\ $$

Question Number 167380 Answers: 0 Comments: 3

show that A′ ∪ B′ ∪ C′ =(A∪B∪C)′

$$\:\boldsymbol{{show}}\:\boldsymbol{{that}} \\ $$$$\:\boldsymbol{{A}}'\:\cup\:\boldsymbol{{B}}'\:\cup\:\boldsymbol{{C}}'\:=\left(\boldsymbol{{A}}\cup\boldsymbol{{B}}\cup\boldsymbol{{C}}\right)' \\ $$

Question Number 167374 Answers: 2 Comments: 0

Question Number 167372 Answers: 1 Comments: 0

Calculate ∫_(−2) ^2 (∣x∣+x)e^(−∣x∣) dx

$${Calculate}\: \\ $$$$\int_{−\mathrm{2}} ^{\mathrm{2}} \left(\mid{x}\mid+{x}\right){e}^{−\mid{x}\mid} {dx} \\ $$

Question Number 167366 Answers: 0 Comments: 0

Question Number 167367 Answers: 1 Comments: 1

Question Number 167360 Answers: 1 Comments: 0

∫(dx/(1+(√x)+(√(1+x))))

$$\int\frac{{dx}}{\mathrm{1}+\sqrt{{x}}+\sqrt{\mathrm{1}+{x}}} \\ $$

Question Number 167357 Answers: 1 Comments: 0

find n^(th) dervaiteve of ln(cosx) ?

$${find}\:{n}^{{th}} \:{dervaiteve}\:{of}\:{ln}\left({cosx}\right)\:? \\ $$

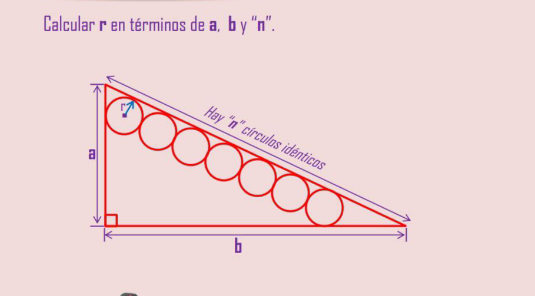
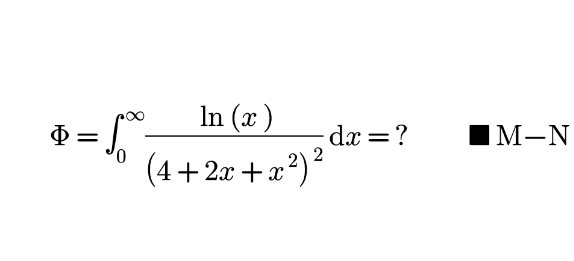
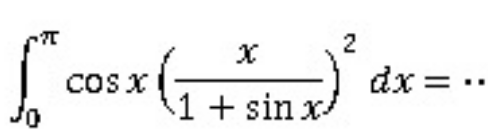
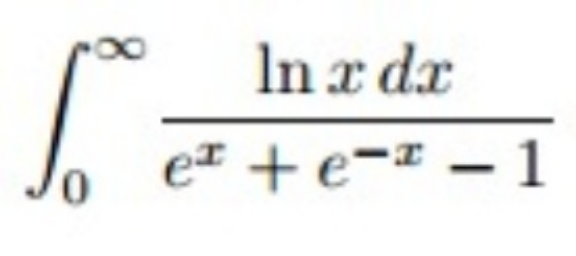
Question Number 167355 Answers: 0 Comments: 4

Question Number 167350 Answers: 1 Comments: 0

Question Number 167339 Answers: 2 Comments: 1

Question Number 167336 Answers: 1 Comments: 0

0< x<(π/2) f(x)= ((sin(x) ))^(1/(20)) + ((cos(x)))^(1/(20)) R_( f) =? (Range )

$$ \\ $$$$\:\:\:\:\:\:\:\:\mathrm{0}<\:{x}<\frac{\pi}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:{f}\left({x}\right)=\:\sqrt[{\mathrm{20}}]{{sin}\left({x}\right)\:\:\:}\:+\:\sqrt[{\mathrm{20}}]{{cos}\left({x}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:{R}_{\:{f}} \:=?\:\:\left({Range}\:\right) \\ $$$$ \\ $$

Question Number 167335 Answers: 2 Comments: 3

x_n =n∙sin(2πen!) Calculate lim_(n→∞) x_n

$$\mathrm{x}_{\mathrm{n}} =\mathrm{n}\centerdot\mathrm{sin}\left(\mathrm{2}\pi\mathrm{en}!\right) \\ $$$$\mathrm{Calculate} \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}x}_{\mathrm{n}} \\ $$

Question Number 167334 Answers: 2 Comments: 0

b^b .2^b^b^2 = 4 ⇒b=?

$$\:\:\:\:{b}^{{b}} .\mathrm{2}^{{b}^{{b}^{\mathrm{2}} } } \:=\:\mathrm{4}\:\Rightarrow{b}=? \\ $$

Pg 508 Pg 509 Pg 510 Pg 511 Pg 512 Pg 513 Pg 514 Pg 515 Pg 516 Pg 517

Contact: info@tinkutara.com