Question and Answers Forum

AllQuestion and Answers: Page 512

Question Number 168179 Answers: 1 Comments: 0

Question Number 168176 Answers: 1 Comments: 0

If , f(x)=(( ∣ sin(2x)∣)/(∣sin(x)∣+∣cos(x)∣ +1)) then : R_( f) =? ( range )

$$ \\ $$$$\:\:\: \\ $$$$\:\:\:\mathrm{I}{f}\:,\:\:{f}\left({x}\right)=\frac{\:\:\mid\:{sin}\left(\mathrm{2}{x}\right)\mid}{\mid{sin}\left({x}\right)\mid+\mid{cos}\left({x}\right)\mid\:+\mathrm{1}} \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{then}\:\::\:\:\:\:\:\:{R}_{\:{f}} \:=?\:\:\:\:\:\:\:\:\left(\:{range}\:\right)\:\: \\ $$$$\:\:\:\:\:\: \\ $$

Question Number 168164 Answers: 0 Comments: 1

Find the total energy (in Joules) of a particle of mass 4.0×10^(−11) kg moving at 80% the speed of light.

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{total}\:\mathrm{energy}\:\left({in}\:{Joules}\right) \\ $$$$\mathrm{of}\:\mathrm{a}\:\mathrm{particle}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{4}.\mathrm{0}×\mathrm{10}^{−\mathrm{11}} \mathrm{kg} \\ $$$$\mathrm{moving}\:\mathrm{at}\:\mathrm{80\%}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{light}. \\ $$

Question Number 168161 Answers: 1 Comments: 1

Question Number 168159 Answers: 0 Comments: 0

Question Number 168158 Answers: 0 Comments: 0

Question Number 168157 Answers: 0 Comments: 0

Question Number 168147 Answers: 0 Comments: 0

calculate :: lim_(x→0) (((tan (1+tan x))/(tan (1+sin x))))^(1/x^3 ) =?

$$\mathrm{calculate}\:\:::\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\sqrt[{\mathrm{x}^{\mathrm{3}} }]{\frac{\mathrm{tan}\:\left(\mathrm{1}+\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{tan}\:\left(\mathrm{1}+\mathrm{sin}\:\mathrm{x}\right)}}=? \\ $$

Question Number 168144 Answers: 1 Comments: 0

lim_(x→0) ((x^3 (√(1+x)) −sin^3 x −(1/2)x^3 tan x)/((((1+2x^3 ))^(1/3) −1)ln (1+x^2 )))=?

$$\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} \sqrt{\mathrm{1}+{x}}\:−\mathrm{sin}\:^{\mathrm{3}} {x}\:−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{3}} \:\mathrm{tan}\:{x}}{\left(\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{2}{x}^{\mathrm{3}} }−\mathrm{1}\right)\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}=?\:\:\:\:\:\:\:\: \\ $$

Question Number 168143 Answers: 2 Comments: 0

lim_(x→0) ((1−cos (1−cos x))/x^4 ) =?

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{1}−\mathrm{cos}\:{x}\right)}{{x}^{\mathrm{4}} }\:=?\:\:\:\:\:\: \\ $$

Question Number 168138 Answers: 2 Comments: 0

Question Number 168131 Answers: 2 Comments: 1

Question Number 168121 Answers: 1 Comments: 0

Question Number 168119 Answers: 1 Comments: 0

Question Number 168118 Answers: 1 Comments: 0

If tan(θ+iφ)=cosα+isinα, prove that : θ=((nΠ)/2)+(Π/4) and φ=(1/2)log tan((Π/4)+(α/2))

$${If}\:{tan}\left(\theta+{i}\phi\right)={cos}\alpha+{isin}\alpha,\: \\ $$$${prove}\:{that}\::\:\theta=\frac{{n}\Pi}{\mathrm{2}}+\frac{\Pi}{\mathrm{4}}\:{and}\:\phi=\frac{\mathrm{1}}{\mathrm{2}}{log}\:{tan}\left(\frac{\Pi}{\mathrm{4}}+\frac{\alpha}{\mathrm{2}}\right) \\ $$

Question Number 168115 Answers: 0 Comments: 2

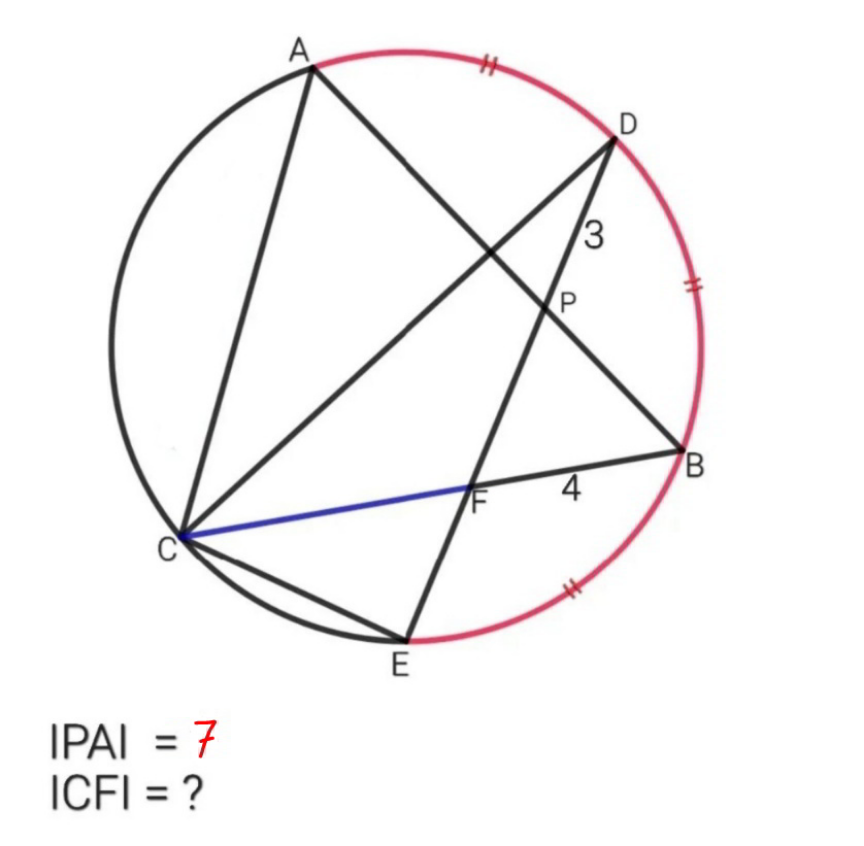
Question Number 168114 Answers: 2 Comments: 0

Question Number 168094 Answers: 1 Comments: 0

Question Number 168093 Answers: 1 Comments: 0

Question Number 168092 Answers: 0 Comments: 0

Question Number 168091 Answers: 0 Comments: 0

Question Number 168090 Answers: 0 Comments: 0

Question Number 168086 Answers: 1 Comments: 0

Question Number 168085 Answers: 0 Comments: 1

Question Number 168084 Answers: 3 Comments: 3

solve in R arcsin(x)+arcsin((√(1−x^2 )))=(π/2)

$${solve}\:{in}\:\mathbb{R} \\ $$$${arcsin}\left({x}\right)+{arcsin}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)=\frac{\pi}{\mathrm{2}} \\ $$

Question Number 168081 Answers: 0 Comments: 0

A cook puts 9.00 g of water in a 2.00L pressure cooker that is then warmed to 500 degree C. What is the pressure inside the container A. 1.89 times 106Pa B. 1.89times 105Pa C. 1.99 times 104Pa D. 1.89 times 103P a E. 1.99 times 109Pa

$$ \\ $$$$\mathrm{A}\:\mathrm{cook}\:\mathrm{puts}\:\mathrm{9}.\mathrm{00}\:\mathrm{g}\:\mathrm{of}\:\mathrm{water}\:\mathrm{in}\:\mathrm{a}\:\mathrm{2}.\mathrm{00L}\:\mathrm{pressure}\:\mathrm{cooker}\: \\ $$$$\mathrm{th}{a}\mathrm{t}\:\mathrm{is}\:\mathrm{then}\:\mathrm{warmed}\:\mathrm{to}\:\mathrm{500}\:\mathrm{degree}\:\mathrm{C}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{pressur}{e}\:\mathrm{inside}\:\mathrm{the}\:\mathrm{container}\:\mathrm{A}.\:\mathrm{1}.\mathrm{89}\:\mathrm{times}\:\mathrm{106Pa}\:\mathrm{B}.\: \\ $$$$\mathrm{1}.\mathrm{89times}\:\mathrm{105Pa}\:\mathrm{C}.\:\mathrm{1}.\mathrm{99}\:\mathrm{times}\:\mathrm{104Pa}\:\mathrm{D}.\:\mathrm{1}.\mathrm{89}\:\mathrm{times}\:\mathrm{103P} \\ $$$$\mathrm{a}\:\mathrm{E}.\:\mathrm{1}.\mathrm{99}\:\mathrm{times}\:\mathrm{109Pa} \\ $$

Pg 507 Pg 508 Pg 509 Pg 510 Pg 511 Pg 512 Pg 513 Pg 514 Pg 515 Pg 516

Contact: info@tinkutara.com