Question and Answers Forum

All Questions   Topic List

AllQuestion and Answers: Page 509

Question Number 161646    Answers: 0   Comments: 0

Question Number 161644    Answers: 0   Comments: 2

there is no single greater than symbol the closest to such a symbol is ≪ or ≫ when is tinku tara going to add the single arrow its a very common symbol and should be on this keyboard

$$\: \\ $$$$\:\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{single}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{symbol}\:\: \\ $$$$\:\mathrm{the}\:\mathrm{closest}\:\mathrm{to}\:\mathrm{such}\:\mathrm{a}\:\mathrm{symbol}\:\mathrm{is}\:\ll\:\mathrm{or}\:\gg\:\: \\ $$$$\:\mathrm{when}\:\mathrm{is}\:\mathrm{tinku}\:\mathrm{tara}\:\mathrm{going}\:\mathrm{to}\:\mathrm{add}\:\mathrm{the}\:\mathrm{single}\:\mathrm{arrow}\:\: \\ $$$$\:\mathrm{its}\:\mathrm{a}\:\mathrm{very}\:\mathrm{common}\:\mathrm{symbol}\:\mathrm{and}\:\mathrm{should}\:\mathrm{be}\:\mathrm{on}\:\mathrm{this}\:\mathrm{keyboard}\:\: \\ $$$$\: \\ $$$$\: \\ $$

Question Number 161629    Answers: 0   Comments: 0

Question Number 161626    Answers: 3   Comments: 1

Question Number 161668    Answers: 1   Comments: 0

Question Number 161623    Answers: 2   Comments: 0

Σ_(n=1) ^∞ (((−1)^(n+1) )/(n(n+2)))=?

$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}+\mathrm{1}} }{\boldsymbol{{n}}\left(\boldsymbol{{n}}+\mathrm{2}\right)}=? \\ $$

Question Number 161622    Answers: 1   Comments: 0

Σ_(n=1) ^∞ (((−1)^(n+1) )/(n(2n+1)))=?

$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}+\mathrm{1}} }{\boldsymbol{{n}}\left(\mathrm{2}\boldsymbol{{n}}+\mathrm{1}\right)}=? \\ $$

Question Number 161617    Answers: 2   Comments: 0

Question Number 161612    Answers: 2   Comments: 0

lim_(x→0^+ ) ((cos (√x)))^(1/x) =?

$$\:\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\sqrt[{{x}}]{\mathrm{cos}\:\sqrt{{x}}}\:=? \\ $$

Question Number 161609    Answers: 0   Comments: 0

∫_0 ^1 ((xln(1+x^4 ))/(1+x^2 ))dx=?

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{xln}}\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{4}} \right)}{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }\boldsymbol{{dx}}=? \\ $$$$ \\ $$

Question Number 161590    Answers: 2   Comments: 0

f(x)=(1/(1−(√x))) + (1/(1−(√(1−x)))) f(x)_(min) = ?

$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−\sqrt{{x}}}\:+\:\frac{\mathrm{1}}{\mathrm{1}−\sqrt{\mathrm{1}−\boldsymbol{{x}}}} \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)_{\boldsymbol{{min}}} =\:? \\ $$

Question Number 161586    Answers: 2   Comments: 2

lim_(x→2^− ) ((2−2cos (√(x−2)))/((x−2)^2 )) =?

$$\:\:\underset{{x}\rightarrow\mathrm{2}^{−} } {\mathrm{lim}}\:\frac{\mathrm{2}−\mathrm{2cos}\:\sqrt{{x}−\mathrm{2}}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }\:=? \\ $$

Question Number 161583    Answers: 3   Comments: 1

lim_(x→2) ((1−sin (π/x))/(x^2 −4x+4)) =? lim_(x→2) ((x^3 −8+sin πx)/(2−x))=? lim_(x→1) ((x^2 −1)/(cos ((π/(x+1)))))=?

$$\:\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{sin}\:\frac{\pi}{{x}}}{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}}\:=? \\ $$$$\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} −\mathrm{8}+\mathrm{sin}\:\pi{x}}{\mathrm{2}−{x}}=? \\ $$$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{cos}\:\left(\frac{\pi}{{x}+\mathrm{1}}\right)}=? \\ $$

Question Number 161578    Answers: 1   Comments: 1

Question Number 161579    Answers: 1   Comments: 1

A gardener wishes to make a rectangular hen run of area 128m² against a wall which is to serve as one of the boundaries. Find the length of the wire netting required for the other three sides

$$ \\ $$A gardener wishes to make a rectangular hen run of area 128m² against a wall which is to serve as one of the boundaries. Find the length of the wire netting required for the other three sides

Question Number 161575    Answers: 1   Comments: 0

∫_0 ^9 ((√x)/(1−x))dx=?

$$\int_{\mathrm{0}} ^{\mathrm{9}} \frac{\sqrt{{x}}}{\mathrm{1}−{x}}{dx}=? \\ $$$$ \\ $$

Question Number 161764    Answers: 2   Comments: 5

Question Number 161567    Answers: 2   Comments: 0

let f(x) be f(x) = (x/(ln(1 - x))) prove there exists a sequence {a_k } such that D[f(x)] = [Σ_0 ^( ∞) a_k x^k ] [f(x)]^2

$$\mathrm{let}\:\:\mathrm{f}\left(\mathrm{x}\right)\:\:\mathrm{be} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{x}}{\mathrm{ln}\left(\mathrm{1}\:-\:\mathrm{x}\right)} \\ $$$$\mathrm{prove}\:\mathrm{there}\:\mathrm{exists}\:\mathrm{a}\:\mathrm{sequence}\:\left\{\mathrm{a}_{\boldsymbol{\mathrm{k}}} \right\}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{D}\left[\mathrm{f}\left(\mathrm{x}\right)\right]\:=\:\left[\underset{\mathrm{0}} {\overset{\:\infty} {\sum}}\:\mathrm{a}_{\boldsymbol{\mathrm{k}}} \:\mathrm{x}^{\boldsymbol{\mathrm{k}}} \right]\:\left[\mathrm{f}\left(\mathrm{x}\right)\right]^{\mathrm{2}} \\ $$

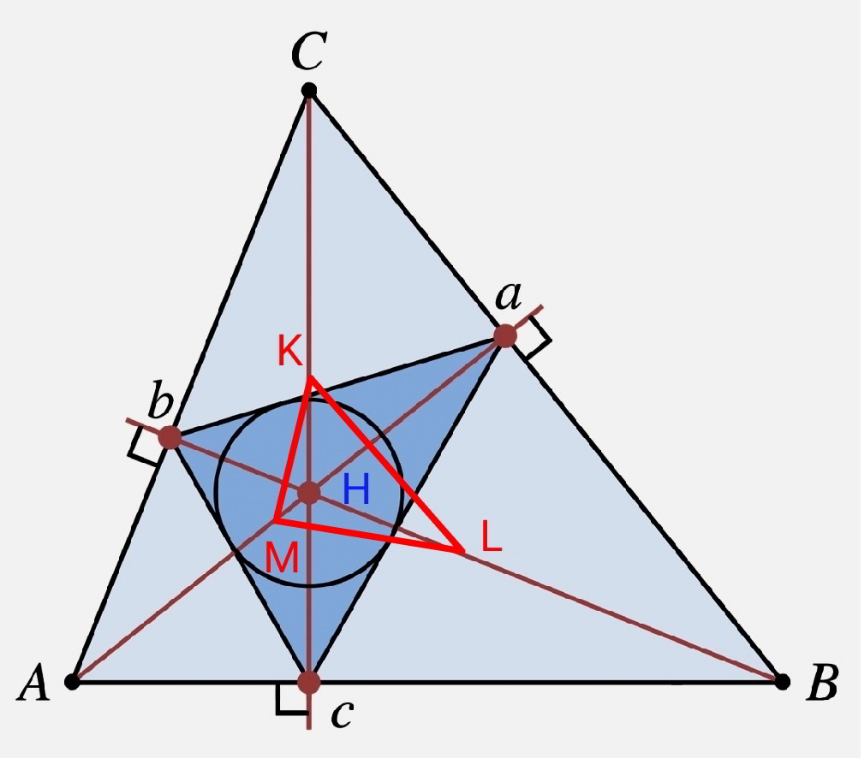
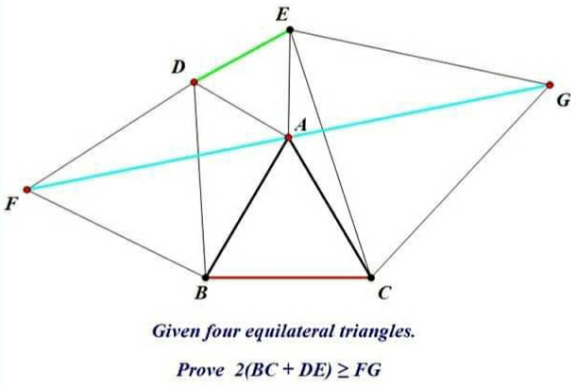
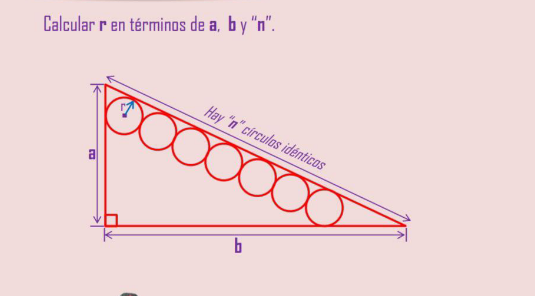
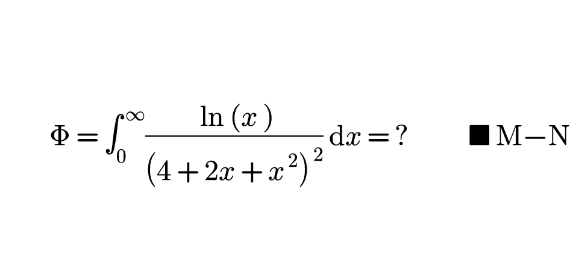
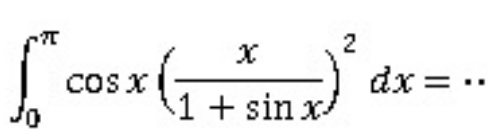
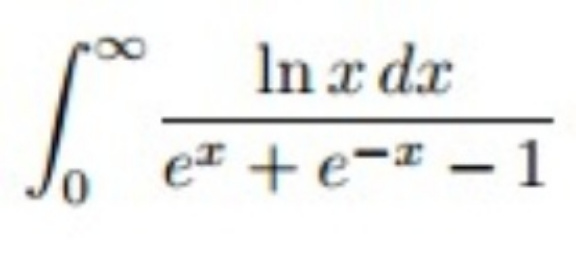
Question Number 161566    Answers: 0   Comments: 0

if x;y;z>0 then prove that: Σ (x/( ((y^3 + 25xyz + z^3 ))^(1/3) )) ≥ 1

$$\mathrm{if}\:\:\mathrm{x};\mathrm{y};\mathrm{z}>\mathrm{0}\:\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\Sigma\:\frac{\mathrm{x}}{\:\sqrt[{\mathrm{3}}]{\mathrm{y}^{\mathrm{3}} \:+\:\mathrm{25xyz}\:+\:\mathrm{z}^{\mathrm{3}} }}\:\geqslant\:\mathrm{1} \\ $$

Question Number 161564    Answers: 1   Comments: 1

Find all values x;y;z>0 such that: { ((x + y + 2z = 6)),(((3/y)∙((2/x) + (1/y)) = 4∙((2/(x + y)) + (1/(2y)))^2 )),((x + 2^y + log_2 z = 4)) :}

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{values}\:\:\mathrm{x};\mathrm{y};\mathrm{z}>\mathrm{0}\:\:\mathrm{such}\:\mathrm{that}: \\ $$$$\begin{cases}{\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{2z}\:=\:\mathrm{6}}\\{\frac{\mathrm{3}}{\mathrm{y}}\centerdot\left(\frac{\mathrm{2}}{\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{y}}\right)\:=\:\mathrm{4}\centerdot\left(\frac{\mathrm{2}}{\mathrm{x}\:+\:\mathrm{y}}\:+\:\frac{\mathrm{1}}{\mathrm{2y}}\right)^{\mathrm{2}} }\\{\mathrm{x}\:+\:\mathrm{2}^{\boldsymbol{\mathrm{y}}} \:+\:\mathrm{log}_{\mathrm{2}} \boldsymbol{\mathrm{z}}\:=\:\mathrm{4}}\end{cases} \\ $$

Question Number 161563    Answers: 1   Comments: 0

Solve the equation: x+(√(x+(√(x+(√(x+ ...)))))) = x∙(√(x∙(√(x∙(√(x∙ ...)))))) where , x>0

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\:...}}}\:=\:\mathrm{x}\centerdot\sqrt{\mathrm{x}\centerdot\sqrt{\mathrm{x}\centerdot\sqrt{\mathrm{x}\centerdot\:...}}} \\ $$$$\mathrm{where}\:,\:\mathrm{x}>\mathrm{0} \\ $$

Question Number 161560    Answers: 1   Comments: 0

lim_(x→+∞) 1+x^2 −2x^2 ln(x)=...?

$${li}\underset{{x}\rightarrow+\infty} {{m}}\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} {ln}\left({x}\right)=...? \\ $$

Question Number 161559    Answers: 1   Comments: 0

please show that (1/2) + cosx + cos2x + cos3x + ... + cosnx = ((sin[(n+1)(x/2)])/(2sin(x/2)))

$${please}\:{show}\:{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:+\:{cosx}\:+\:{cos}\mathrm{2}{x}\:+\:{cos}\mathrm{3}{x}\:+\:...\:+\:{cosnx}\:=\:\frac{{sin}\left[\left({n}+\mathrm{1}\right)\frac{{x}}{\mathrm{2}}\right]}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$

Question Number 161558    Answers: 1   Comments: 0

What′s the value of a for which x^2 +x=a & x^2 −3x+2=a have one root common?

$${What}'{s}\:{the}\:{value}\:{of}\:{a}\:{for}\:{which} \\ $$$${x}^{\mathrm{2}} +{x}={a}\:\&\:{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}={a}\:{have}\:{one} \\ $$$${root}\:{common}? \\ $$

Question Number 161553    Answers: 0   Comments: 0

lim_(t→+∞) tΣ_(k=0) ^∞ (((−1)^k )/( (√(k^2 +t^2 ))))=?

$$\underset{\mathrm{t}\rightarrow+\infty} {\mathrm{lim}t}\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\:\sqrt{\mathrm{k}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }}=? \\ $$

Question Number 161537    Answers: 2   Comments: 0

∫_0 ^( (π/4)) ((1+tan^4 (x))/(cot^2 (x))) dx =?

$$\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} \left({x}\right)}{\mathrm{cot}\:^{\mathrm{2}} \left({x}\right)}\:{dx}\:=? \\ $$

  Pg 504      Pg 505      Pg 506      Pg 507      Pg 508      Pg 509      Pg 510      Pg 511      Pg 512      Pg 513   

Terms of Service

Privacy Policy

Contact: info@tinkutara.com