Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 507

Question Number 168097 Answers: 0 Comments: 0

Question Number 167449 Answers: 0 Comments: 1

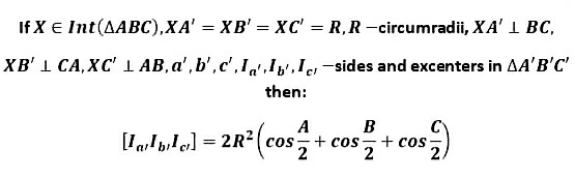
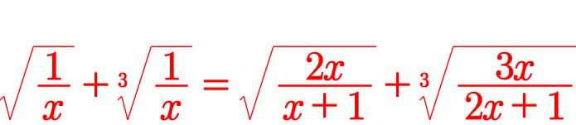
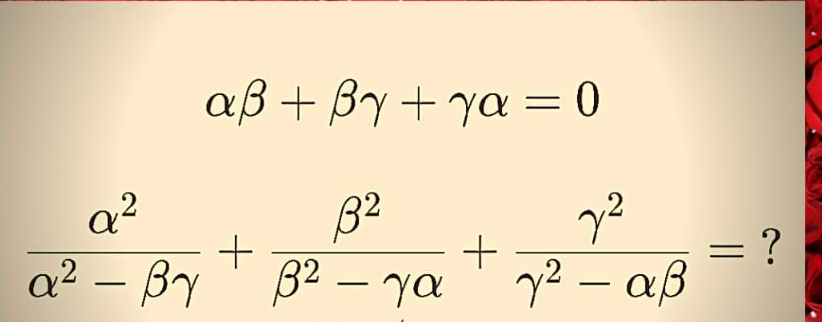
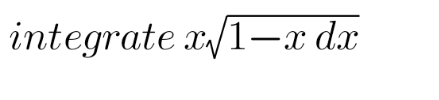
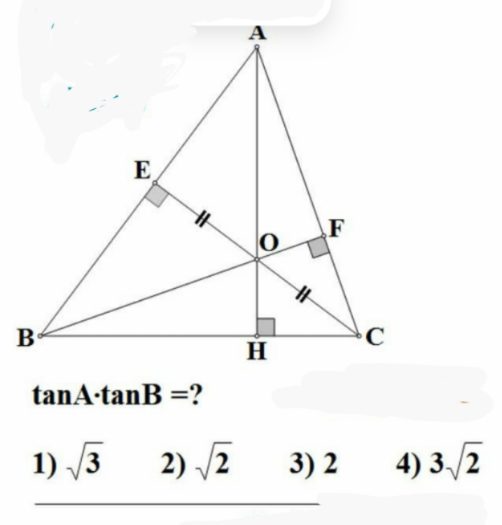
Question Number 167448 Answers: 0 Comments: 2

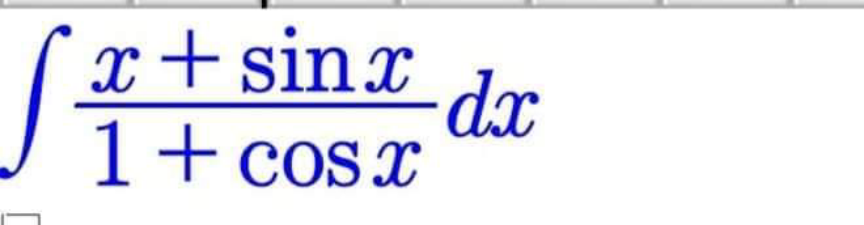
Question Number 167441 Answers: 0 Comments: 0

Question Number 167438 Answers: 2 Comments: 0

∫ ((sin 4x)/(4sin^4 x−4sin^2 x+1)) dx=?

$$\:\:\int\:\frac{\mathrm{sin}\:\mathrm{4x}}{\mathrm{4sin}\:^{\mathrm{4}} \mathrm{x}−\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{1}}\:\mathrm{dx}=? \\ $$

Question Number 167439 Answers: 0 Comments: 1

Question Number 167434 Answers: 2 Comments: 0

lim_(x→a) ((x^n −a^n −na^(n−1) (x−a))/((x−a)^2 ))=?

$$\:\:\:\:\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{x}^{{n}} −{a}^{{n}} −{na}^{{n}−\mathrm{1}} \left({x}−{a}\right)}{\left({x}−{a}\right)^{\mathrm{2}} }=? \\ $$

Question Number 167433 Answers: 0 Comments: 0

calculate 1 : Ω= Σ_(n=1) ^∞ ((( H_( n) )/n) )^( 2) = ? 2 : ∫_0 ^( 1) ((ln^( 2) (x).Li_( 2) (x))/x) dx = ?

$$ \\ $$$$\:\:\:\:\:\:\:{calculate}\: \\ $$$$\:\:\:\:\mathrm{1}\::\:\:\Omega=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\:{H}_{\:{n}} }{{n}}\:\right)^{\:\mathrm{2}} =\:? \\ $$$$\:\:\:\:\mathrm{2}\::\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{ln}^{\:\mathrm{2}} \left({x}\right).\mathrm{L}{i}_{\:\mathrm{2}} \left({x}\right)}{{x}}\:{dx}\:=\:? \\ $$$$ \\ $$

Question Number 167426 Answers: 0 Comments: 1

∫ ((sec^2 x)/(x^2 +1)) dx

$$\int\:\frac{{sec}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$

Question Number 167421 Answers: 1 Comments: 0

Question Number 167419 Answers: 1 Comments: 1

((1/2))!=? Use Method and Formula!!!!!!!!!

$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)!=? \\ $$$${Use}\:{Method}\:{and}\:{Formula}!!!!!!!!! \\ $$

Question Number 167418 Answers: 0 Comments: 0

x^y =z (z)^(1/y) =x log_x (z)=y

$${x}^{{y}} ={z} \\ $$$$\sqrt[{{y}}]{{z}}={x} \\ $$$$\mathrm{log}_{{x}} \left({z}\right)={y} \\ $$

Question Number 167416 Answers: 0 Comments: 3

∫_( 0) ^( π) ((x.sin (x))/(1+cos^2 (x) ))dx ∫_0 ^( π) (1/(1+cos^3 (x) +sin^3 (x) ))dx ∫_0 ^(π/2) ((x.cos(x)sin(x))/(tan^2 (x)+ cot^2 (x) ))dx ∫_0 ^( 1) tan^(−1) ((√(1−x^2 )))dx

$$\int_{\:\mathrm{0}} ^{\:\pi} \:\frac{{x}.\mathrm{sin}\:\left({x}\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \left({x}\right)\:}{dx} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\:\:\pi} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}^{\mathrm{3}} \left({x}\right)\:+\mathrm{sin}^{\mathrm{3}} \left({x}\right)\:}{dx} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{x}.\mathrm{cos}\left(\mathrm{x}\right)\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{tan}^{\mathrm{2}} \left(\mathrm{x}\right)+\:\mathrm{cot}^{\mathrm{2}} \left(\mathrm{x}\right)\:}\mathrm{dx} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$ \\ $$

Question Number 167445 Answers: 0 Comments: 0

Question Number 167404 Answers: 1 Comments: 0

Question Number 167443 Answers: 1 Comments: 0

Question Number 167402 Answers: 0 Comments: 2

find (d^n /dx^n ) [ ln (cosx) ]

$$\boldsymbol{{find}}\:\frac{\boldsymbol{{d}}^{\boldsymbol{{n}}} }{\boldsymbol{{dx}}^{\boldsymbol{{n}}} }\:\left[\:\boldsymbol{{ln}}\:\left(\boldsymbol{{cosx}}\right)\:\right] \\ $$

Question Number 167400 Answers: 2 Comments: 0

Question Number 167393 Answers: 1 Comments: 0

Question Number 167392 Answers: 2 Comments: 0

f(x)=n! ((df(x)^n )/(d(x)^n ))=?

$${f}\left({x}\right)={n}! \\ $$$$\frac{{df}\left({x}\right)^{{n}} }{{d}\left({x}\right)^{{n}} }=? \\ $$

Question Number 167386 Answers: 0 Comments: 0

show that (A⊕B)′ = A ∩ B

$$\:\boldsymbol{{show}}\:\boldsymbol{{that}}\: \\ $$$$\:\left(\boldsymbol{{A}}\oplus\boldsymbol{{B}}\right)'\:=\:\boldsymbol{{A}}\:\cap\:\boldsymbol{{B}} \\ $$

Question Number 167380 Answers: 0 Comments: 3

show that A′ ∪ B′ ∪ C′ =(A∪B∪C)′

$$\:\boldsymbol{{show}}\:\boldsymbol{{that}} \\ $$$$\:\boldsymbol{{A}}'\:\cup\:\boldsymbol{{B}}'\:\cup\:\boldsymbol{{C}}'\:=\left(\boldsymbol{{A}}\cup\boldsymbol{{B}}\cup\boldsymbol{{C}}\right)' \\ $$

Question Number 167374 Answers: 2 Comments: 0

Question Number 167372 Answers: 1 Comments: 0

Calculate ∫_(−2) ^2 (∣x∣+x)e^(−∣x∣) dx

$${Calculate}\: \\ $$$$\int_{−\mathrm{2}} ^{\mathrm{2}} \left(\mid{x}\mid+{x}\right){e}^{−\mid{x}\mid} {dx} \\ $$

Question Number 167366 Answers: 0 Comments: 0

Question Number 167367 Answers: 1 Comments: 1

Pg 502 Pg 503 Pg 504 Pg 505 Pg 506 Pg 507 Pg 508 Pg 509 Pg 510 Pg 511

Contact: info@tinkutara.com