
AllQuestion and Answers: Page 506
Question Number 166223 Answers: 0 Comments: 0

Question Number 166258 Answers: 0 Comments: 0

Question Number 166257 Answers: 1 Comments: 2
Question Number 166212 Answers: 1 Comments: 0
Question Number 166210 Answers: 1 Comments: 0

Question Number 166208 Answers: 2 Comments: 1

Question Number 166246 Answers: 1 Comments: 0

Question Number 166195 Answers: 3 Comments: 0

Question Number 166192 Answers: 1 Comments: 0
$$\:\:\:\:\int\:\frac{{dx}}{\mathrm{5}+\mathrm{4sin}\:{x}}\:=? \\ $$
Question Number 166191 Answers: 1 Comments: 0
Question Number 166186 Answers: 2 Comments: 0
$${if}\:{sin}\theta\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:{find}\:{cos}\theta \\ $$
Question Number 166182 Answers: 2 Comments: 0
Question Number 166181 Answers: 0 Comments: 0
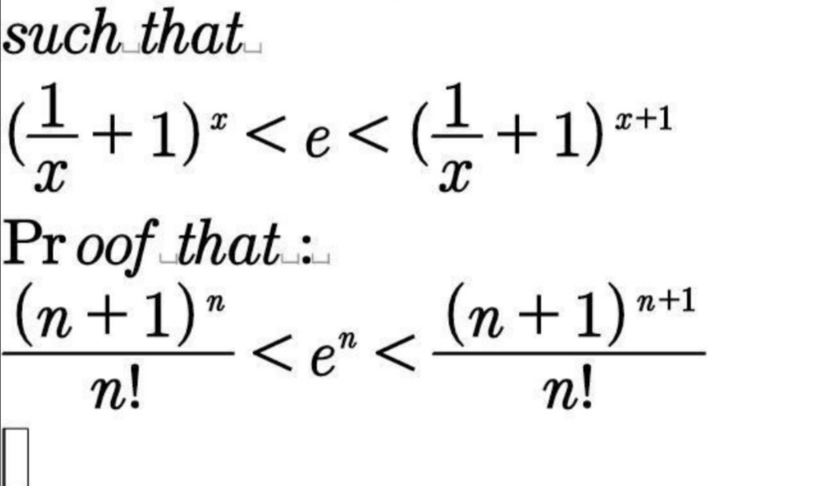
Question Number 166177 Answers: 1 Comments: 0
Question Number 166176 Answers: 0 Comments: 0

Question Number 166170 Answers: 2 Comments: 0
Question Number 166169 Answers: 1 Comments: 0
Question Number 166168 Answers: 0 Comments: 0
Question Number 166167 Answers: 0 Comments: 0

Question Number 166163 Answers: 0 Comments: 0
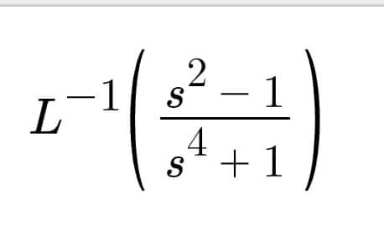
Question Number 166215 Answers: 1 Comments: 0

Question Number 166260 Answers: 1 Comments: 0
Question Number 166160 Answers: 3 Comments: 0
Question Number 166143 Answers: 1 Comments: 0

Question Number 166141 Answers: 2 Comments: 0
Question Number 166137 Answers: 2 Comments: 0
Pg 501 Pg 502 Pg 503 Pg 504 Pg 505 Pg 506 Pg 507 Pg 508 Pg 509 Pg 510
