
AllQuestion and Answers: Page 505
Question Number 169812 Answers: 0 Comments: 0
Question Number 169811 Answers: 0 Comments: 0
Question Number 169809 Answers: 0 Comments: 1
Question Number 169803 Answers: 1 Comments: 0

Question Number 169802 Answers: 1 Comments: 0
Question Number 169800 Answers: 0 Comments: 0
Question Number 169798 Answers: 0 Comments: 2
Question Number 169797 Answers: 3 Comments: 0
Question Number 169792 Answers: 1 Comments: 0
Question Number 169790 Answers: 0 Comments: 0

Question Number 169768 Answers: 0 Comments: 0
Question Number 169765 Answers: 0 Comments: 3

Question Number 169756 Answers: 3 Comments: 0

Question Number 169738 Answers: 3 Comments: 1
$$\mathrm{2}^{{x}} +{x}=\mathrm{11} \\ $$$${find}\:{x}? \\ $$$$ \\ $$$${Mastermind} \\ $$
Question Number 169736 Answers: 0 Comments: 0
Question Number 169733 Answers: 1 Comments: 0
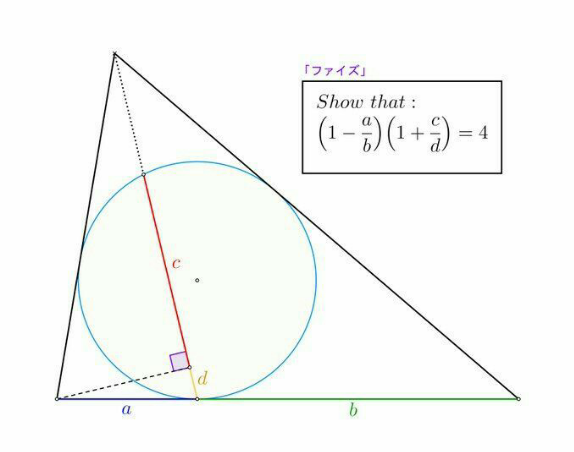
Question Number 169727 Answers: 0 Comments: 6
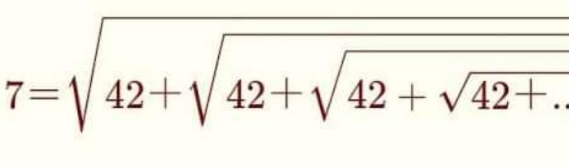
Question Number 169725 Answers: 0 Comments: 0
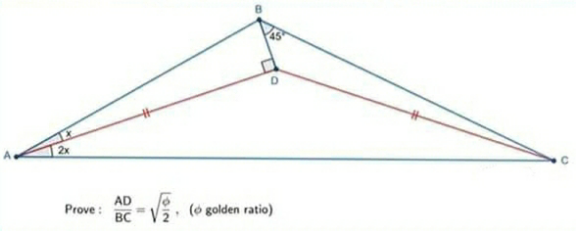
Question Number 169760 Answers: 1 Comments: 0
Question Number 169751 Answers: 0 Comments: 0
Question Number 169745 Answers: 2 Comments: 0

Question Number 169743 Answers: 2 Comments: 0
Question Number 169713 Answers: 0 Comments: 4

Question Number 169712 Answers: 0 Comments: 0
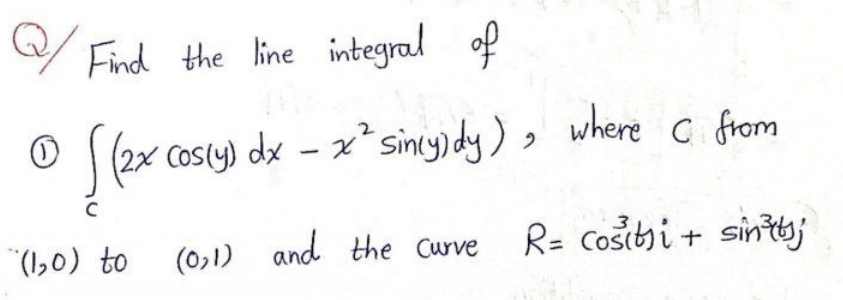
Question Number 169711 Answers: 2 Comments: 3
Question Number 169808 Answers: 0 Comments: 0
Pg 500 Pg 501 Pg 502 Pg 503 Pg 504 Pg 505 Pg 506 Pg 507 Pg 508 Pg 509
