
AllQuestion and Answers: Page 504
Question Number 169906 Answers: 0 Comments: 0
Question Number 170010 Answers: 1 Comments: 1
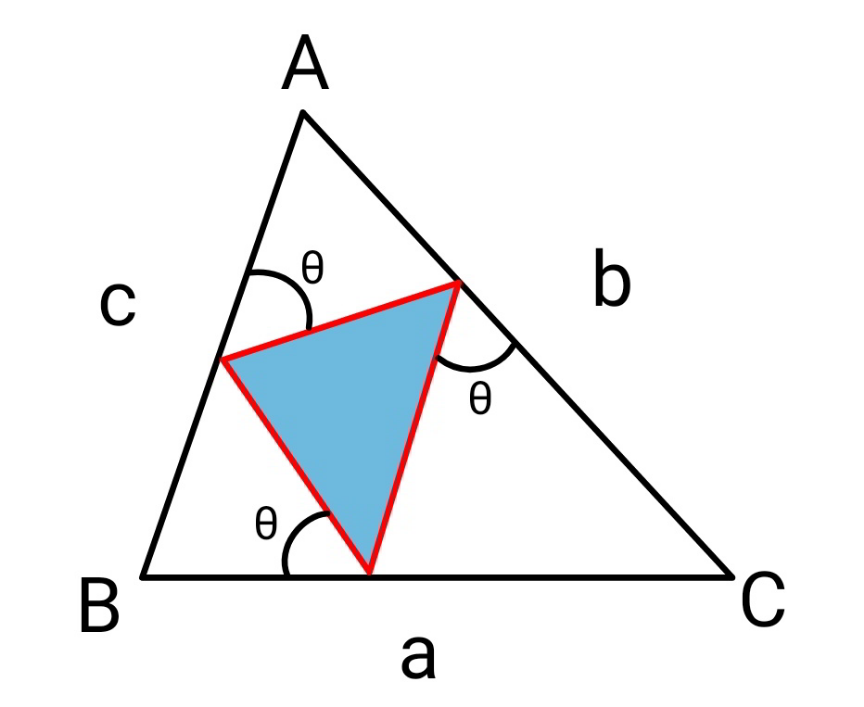
Question Number 170012 Answers: 1 Comments: 0
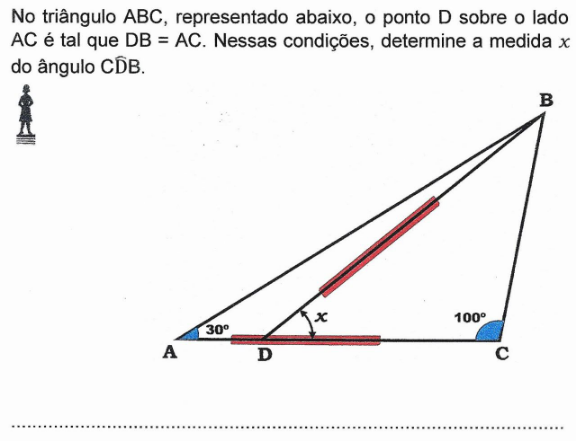
Question Number 169901 Answers: 0 Comments: 0
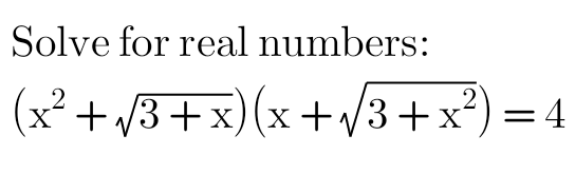
Question Number 169900 Answers: 0 Comments: 0
Question Number 169899 Answers: 1 Comments: 2

Question Number 169897 Answers: 0 Comments: 1

Question Number 169896 Answers: 1 Comments: 0

Question Number 169892 Answers: 1 Comments: 0
$$\frac{{dy}}{{dx}}\:=\:\mathrm{2}{xe}^{−{y}} \:,\:\:{y}\left(\mathrm{1}\right)\:=\:\mathrm{0} \\ $$
Question Number 169885 Answers: 1 Comments: 0
Question Number 169878 Answers: 2 Comments: 0
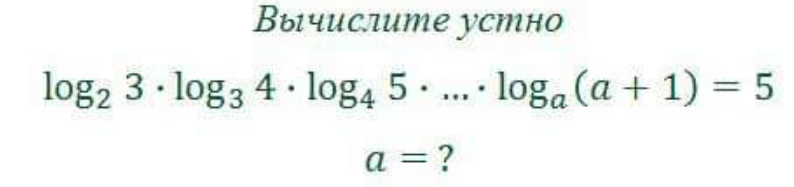
Question Number 169874 Answers: 1 Comments: 0
Question Number 169873 Answers: 2 Comments: 0
Question Number 169870 Answers: 0 Comments: 0
Question Number 169865 Answers: 3 Comments: 2
Question Number 169864 Answers: 1 Comments: 0

Question Number 169863 Answers: 1 Comments: 0
$$\int_{{o}} ^{\mathrm{1}} {xln}\mid{x}^{\mathrm{2}} −\mathrm{2}{x}\mid{dx} \\ $$
Question Number 169860 Answers: 1 Comments: 0
Question Number 169859 Answers: 0 Comments: 0
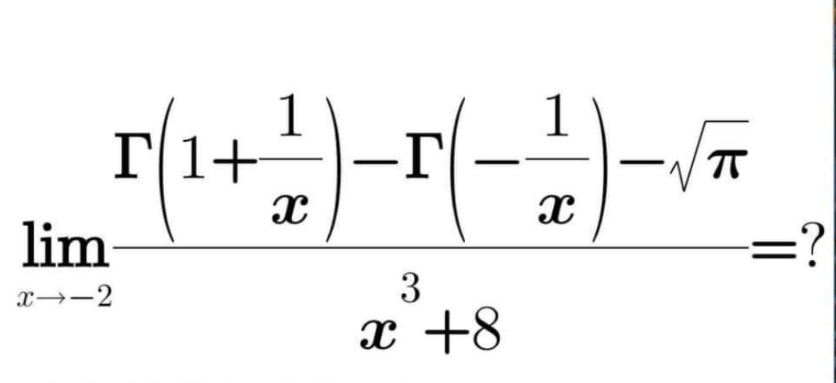
Question Number 169855 Answers: 1 Comments: 0

Question Number 169852 Answers: 1 Comments: 0
Question Number 169850 Answers: 0 Comments: 1

Question Number 169849 Answers: 1 Comments: 0
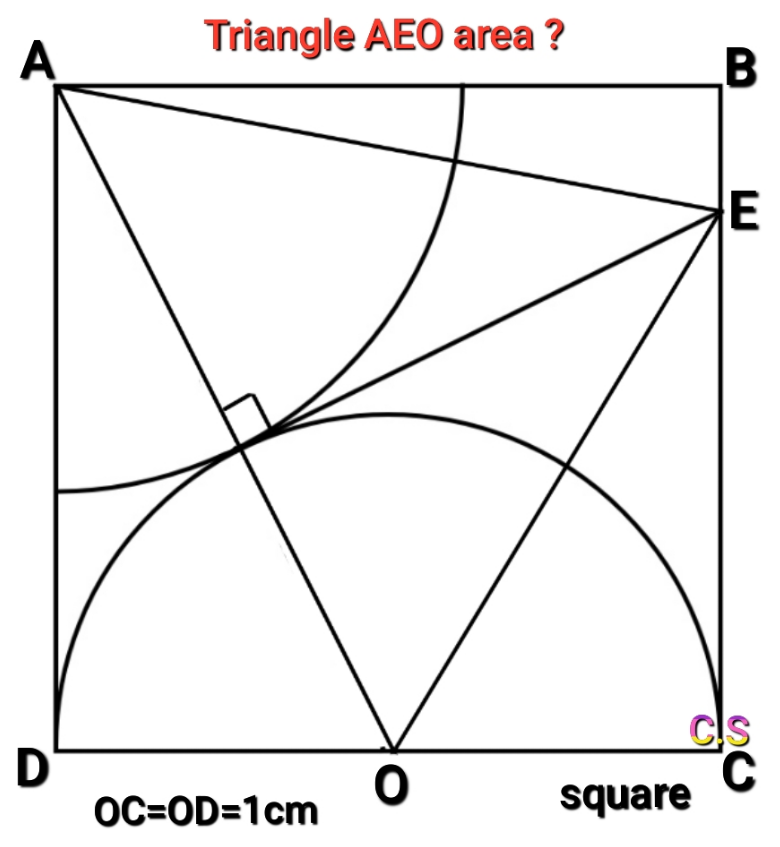
Question Number 169842 Answers: 1 Comments: 0

Question Number 169837 Answers: 0 Comments: 0
Question Number 169836 Answers: 1 Comments: 0

Pg 499 Pg 500 Pg 501 Pg 502 Pg 503 Pg 504 Pg 505 Pg 506 Pg 507 Pg 508
