
AllQuestion and Answers: Page 503
Question Number 169982 Answers: 0 Comments: 0
Question Number 169977 Answers: 1 Comments: 0
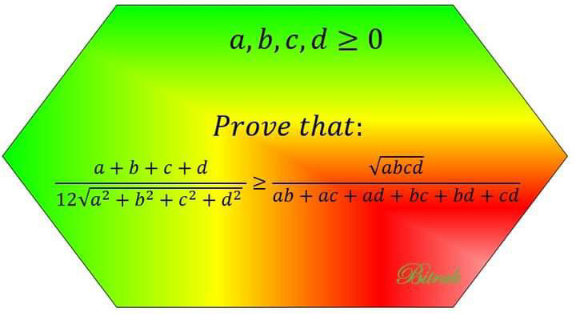
Question Number 169974 Answers: 0 Comments: 1

Question Number 169973 Answers: 1 Comments: 0
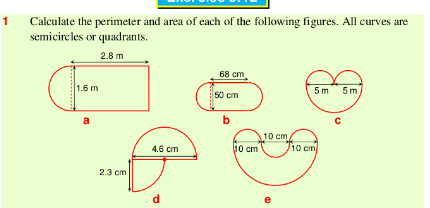
Question Number 169972 Answers: 0 Comments: 0

Question Number 169969 Answers: 1 Comments: 0

Question Number 169966 Answers: 1 Comments: 0
Question Number 169949 Answers: 0 Comments: 7
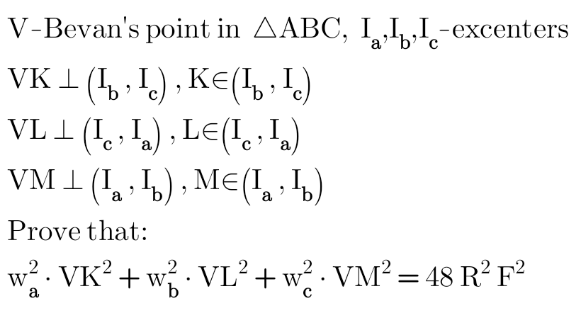
Question Number 169947 Answers: 2 Comments: 1
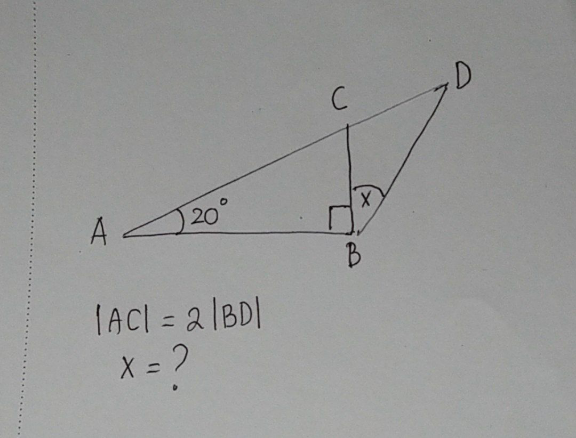
Question Number 169944 Answers: 0 Comments: 1

Question Number 169945 Answers: 1 Comments: 5

Question Number 169942 Answers: 0 Comments: 0

Question Number 170006 Answers: 0 Comments: 0
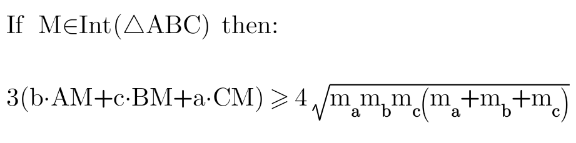
Question Number 170005 Answers: 2 Comments: 3

Question Number 170004 Answers: 0 Comments: 0
Question Number 169932 Answers: 0 Comments: 0
Question Number 169930 Answers: 0 Comments: 0
Question Number 169925 Answers: 0 Comments: 0

Question Number 169924 Answers: 0 Comments: 3

Question Number 169923 Answers: 0 Comments: 0
Question Number 169922 Answers: 1 Comments: 0
Question Number 169920 Answers: 0 Comments: 0

Question Number 169918 Answers: 3 Comments: 0
Question Number 169916 Answers: 1 Comments: 0
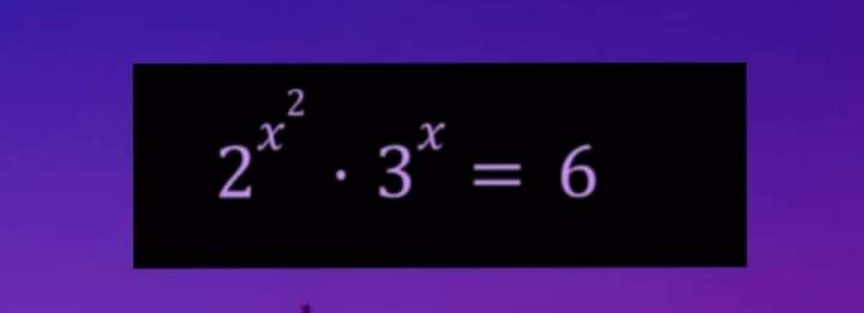
Question Number 169915 Answers: 2 Comments: 0
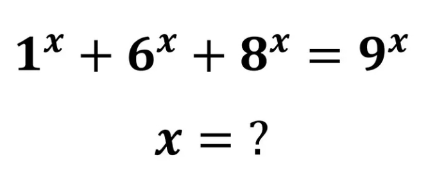
Question Number 169913 Answers: 0 Comments: 1
Pg 498 Pg 499 Pg 500 Pg 501 Pg 502 Pg 503 Pg 504 Pg 505 Pg 506 Pg 507
