
AllQuestion and Answers: Page 502
Question Number 170084 Answers: 0 Comments: 2

Question Number 170079 Answers: 2 Comments: 0
Question Number 170077 Answers: 1 Comments: 0
$$ \\ $$How do I find for the accurate measure of sine from 1 to 30
Question Number 170076 Answers: 0 Comments: 0

Question Number 170075 Answers: 0 Comments: 0

Question Number 170073 Answers: 3 Comments: 3

Question Number 170065 Answers: 1 Comments: 0
Question Number 170064 Answers: 2 Comments: 0
Question Number 170057 Answers: 1 Comments: 0
Question Number 170054 Answers: 1 Comments: 0

Question Number 170053 Answers: 1 Comments: 0
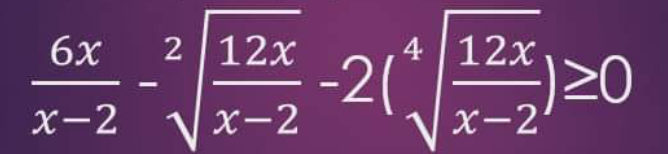
Question Number 170050 Answers: 1 Comments: 0
Question Number 170046 Answers: 2 Comments: 0
Question Number 170032 Answers: 1 Comments: 2
Question Number 170028 Answers: 0 Comments: 1
Question Number 170025 Answers: 1 Comments: 0
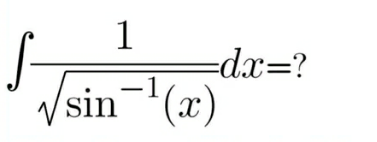
Question Number 170022 Answers: 0 Comments: 0
Question Number 170020 Answers: 0 Comments: 0
Question Number 170018 Answers: 1 Comments: 0
Question Number 170015 Answers: 1 Comments: 0
Question Number 170014 Answers: 1 Comments: 0

Question Number 170003 Answers: 1 Comments: 1
Question Number 169989 Answers: 0 Comments: 0
Question Number 169987 Answers: 1 Comments: 0
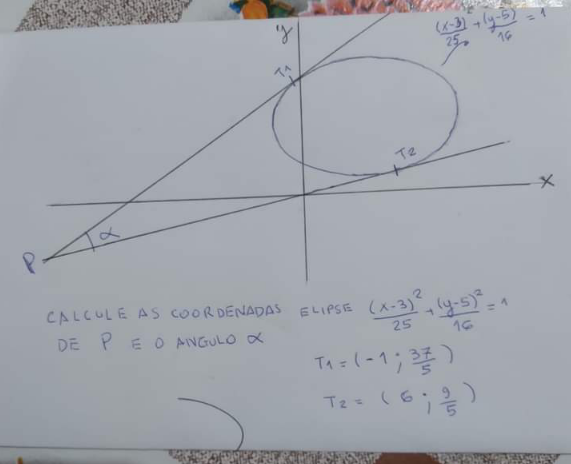
Question Number 169986 Answers: 0 Comments: 0
$$\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}{x}\:−\:\mathrm{3}} \:>\:\mathrm{1} \\ $$
Question Number 169982 Answers: 0 Comments: 0
Pg 497 Pg 498 Pg 499 Pg 500 Pg 501 Pg 502 Pg 503 Pg 504 Pg 505 Pg 506
