
AllQuestion and Answers: Page 501
Question Number 170187 Answers: 1 Comments: 3
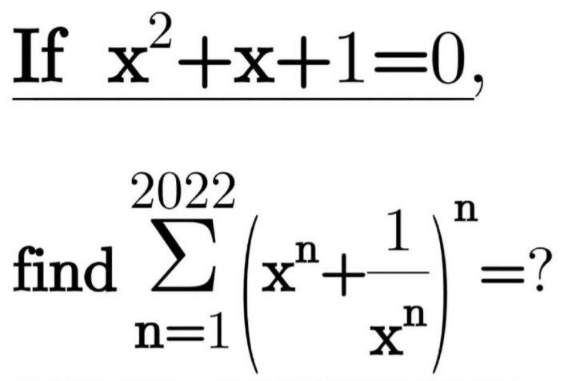
Question Number 170159 Answers: 1 Comments: 0
Question Number 170155 Answers: 1 Comments: 0
Question Number 170154 Answers: 0 Comments: 0
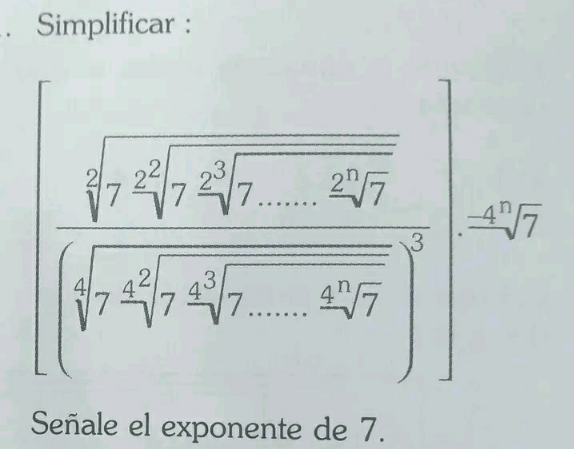
Question Number 170150 Answers: 1 Comments: 0
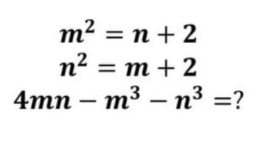
Question Number 170148 Answers: 1 Comments: 0
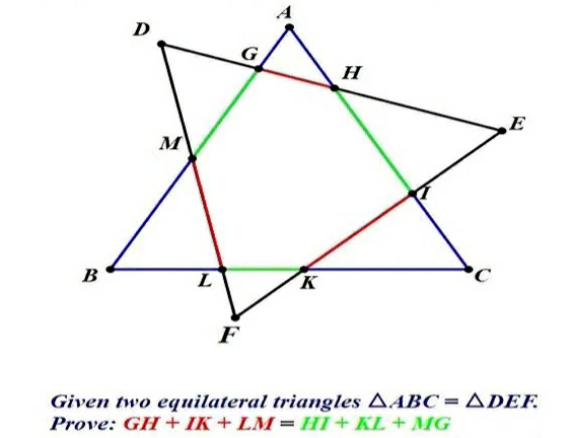
Question Number 170255 Answers: 1 Comments: 0
$$\frac{{d}}{{dx}}\left[\int_{\mathrm{2}} ^{{x}} {e}^{{t}^{\mathrm{2}} } {dt}=?\right. \\ $$
Question Number 170143 Answers: 0 Comments: 3

Question Number 170142 Answers: 0 Comments: 2

Question Number 170141 Answers: 1 Comments: 3
Question Number 170140 Answers: 0 Comments: 0
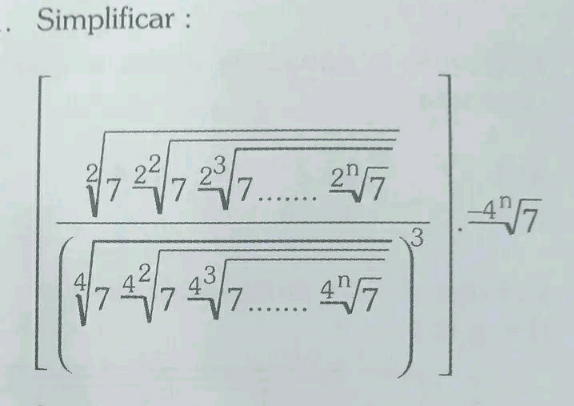
Question Number 170131 Answers: 1 Comments: 0
$$\mathrm{4}^{\mid{x}\mid} ={x}^{\mathrm{4}} \\ $$$${x}=? \\ $$
Question Number 170130 Answers: 0 Comments: 3
Question Number 170129 Answers: 0 Comments: 0
Question Number 170126 Answers: 0 Comments: 3

Question Number 170120 Answers: 1 Comments: 2

Question Number 170117 Answers: 1 Comments: 1
$${x}^{\mathrm{2}} =\mathrm{4}^{{x}} \:\:\:\:\:\:{x}=? \\ $$$$ \\ $$$$ \\ $$
Question Number 170116 Answers: 1 Comments: 1
Question Number 170115 Answers: 0 Comments: 0
Question Number 170113 Answers: 0 Comments: 0

Question Number 170109 Answers: 0 Comments: 0

Question Number 170106 Answers: 1 Comments: 0

Question Number 170110 Answers: 2 Comments: 1
$${prove}\:{that} \\ $$$${e}^{{i}\theta} ={cos}\theta+{isin}\theta \\ $$
Question Number 170091 Answers: 0 Comments: 0

Question Number 170100 Answers: 0 Comments: 1

Question Number 170099 Answers: 0 Comments: 0

Pg 496 Pg 497 Pg 498 Pg 499 Pg 500 Pg 501 Pg 502 Pg 503 Pg 504 Pg 505
