
AllQuestion and Answers: Page 500
Question Number 170275 Answers: 0 Comments: 0

Question Number 170270 Answers: 0 Comments: 3
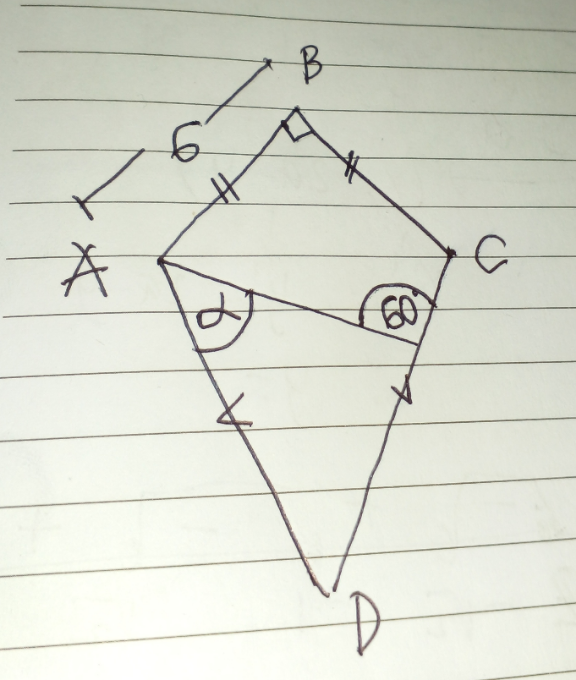
Question Number 170265 Answers: 0 Comments: 1
Question Number 170262 Answers: 0 Comments: 0
Question Number 170259 Answers: 0 Comments: 0

Question Number 170240 Answers: 0 Comments: 0
Question Number 170226 Answers: 1 Comments: 0
Question Number 170221 Answers: 1 Comments: 1
Question Number 170212 Answers: 3 Comments: 0
Question Number 170211 Answers: 1 Comments: 0
Question Number 170206 Answers: 2 Comments: 0
Question Number 170205 Answers: 1 Comments: 0
Question Number 170203 Answers: 1 Comments: 0
$${solve}:\:\mathrm{5}^{{lgx}} =\mathrm{50}−{x}^{{lg}\mathrm{5}} \\ $$
Question Number 170202 Answers: 0 Comments: 10
Question Number 170199 Answers: 1 Comments: 0
Question Number 170198 Answers: 1 Comments: 0
Question Number 170197 Answers: 1 Comments: 0
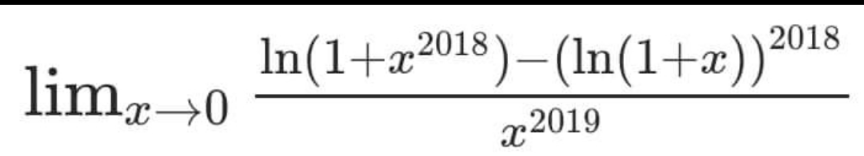
Question Number 170196 Answers: 0 Comments: 0
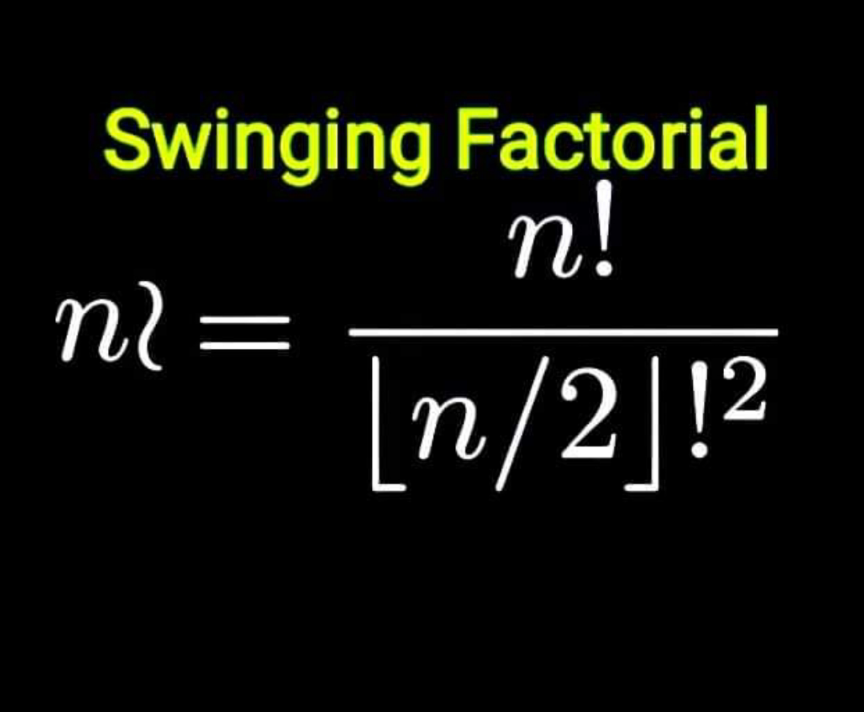
Question Number 170311 Answers: 1 Comments: 0
Question Number 170189 Answers: 0 Comments: 2
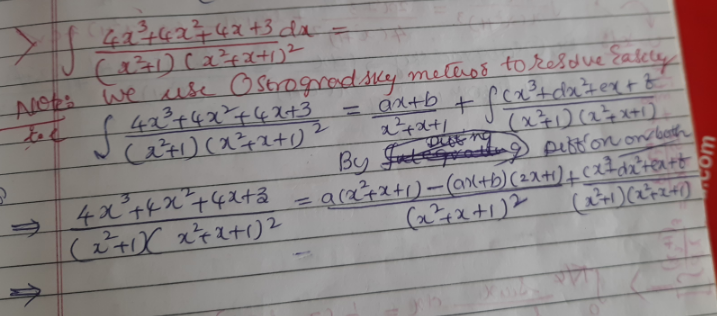
Question Number 170185 Answers: 0 Comments: 1

Question Number 170184 Answers: 0 Comments: 0

Question Number 170183 Answers: 0 Comments: 0

Question Number 170182 Answers: 1 Comments: 1
Question Number 170181 Answers: 1 Comments: 0
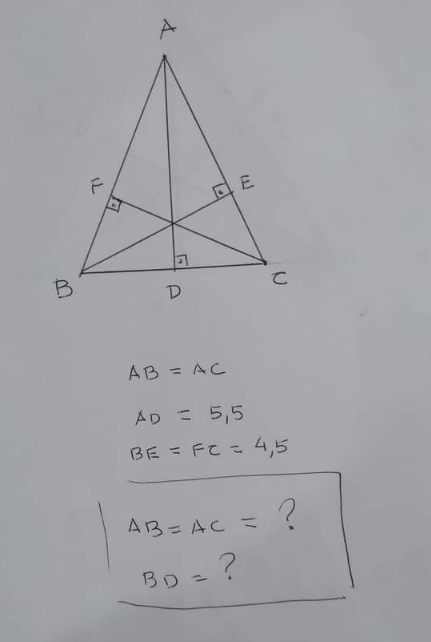
Question Number 170166 Answers: 1 Comments: 1
Pg 495 Pg 496 Pg 497 Pg 498 Pg 499 Pg 500 Pg 501 Pg 502 Pg 503 Pg 504
