
AllQuestion and Answers: Page 493
Question Number 170911 Answers: 1 Comments: 0
Question Number 170910 Answers: 0 Comments: 0

Question Number 170909 Answers: 0 Comments: 4
$$\mathrm{1}!+\mathrm{2}!+\mathrm{3}!+....+\mathrm{20000}!=? \\ $$
Question Number 170906 Answers: 2 Comments: 0

Question Number 170904 Answers: 0 Comments: 0
Question Number 170902 Answers: 0 Comments: 2
Question Number 170900 Answers: 0 Comments: 0

Question Number 170893 Answers: 0 Comments: 0

Question Number 170894 Answers: 0 Comments: 0

Question Number 170891 Answers: 0 Comments: 1

Question Number 170888 Answers: 0 Comments: 0

Question Number 170890 Answers: 2 Comments: 0
Question Number 170889 Answers: 1 Comments: 1

Question Number 170878 Answers: 1 Comments: 0

Question Number 170868 Answers: 1 Comments: 0
Question Number 170856 Answers: 1 Comments: 2
Question Number 170855 Answers: 1 Comments: 0
Question Number 181349 Answers: 0 Comments: 0
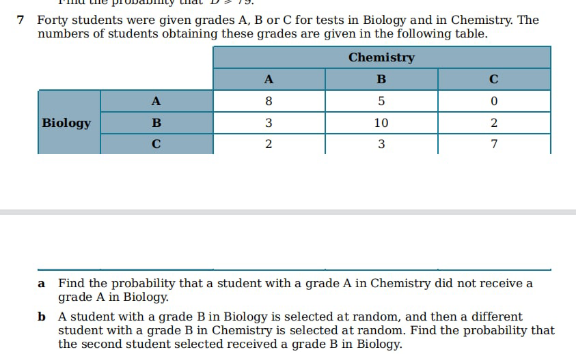
Question Number 170872 Answers: 1 Comments: 0

Question Number 170871 Answers: 1 Comments: 0
Question Number 170849 Answers: 1 Comments: 0
Question Number 170847 Answers: 0 Comments: 1
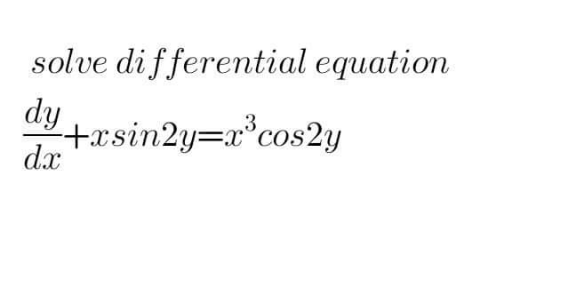
Question Number 170844 Answers: 2 Comments: 0
$${solve}\:{x}^{\mathrm{2}} +\sqrt{\mathrm{3}−{x}}=\mathrm{3} \\ $$
Question Number 170843 Answers: 1 Comments: 0

Question Number 170838 Answers: 1 Comments: 0
Question Number 170836 Answers: 2 Comments: 1
Pg 488 Pg 489 Pg 490 Pg 491 Pg 492 Pg 493 Pg 494 Pg 495 Pg 496 Pg 497
