Question and Answers Forum

AllQuestion and Answers: Page 492

Question Number 170378 Answers: 1 Comments: 0

The line 2y=x+3 meets the circle x^2 +y^2 −2x−6y−15 at point M and N where N is in the second quadrant. find the coordinate of M and N. Mastermind

$${The}\:{line}\:\mathrm{2}{y}={x}+\mathrm{3}\:{meets}\:{the}\:{circle}\: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{6}{y}−\mathrm{15}\:{at}\:{point}\:{M}\:{and}\:{N} \\ $$$${where}\:{N}\:{is}\:{in}\:{the}\:{second}\:{quadrant}. \\ $$$${find}\:{the}\:{coordinate}\:{of}\:{M}\:{and}\:{N}. \\ $$$$ \\ $$$${Mastermind} \\ $$

Question Number 170376 Answers: 0 Comments: 0

Question Number 170374 Answers: 0 Comments: 2

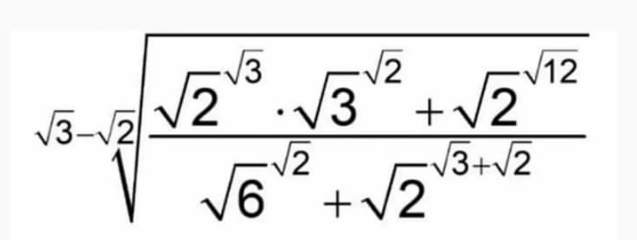
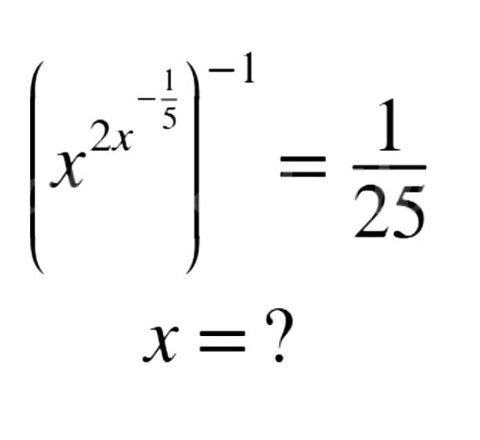
Question Number 170372 Answers: 0 Comments: 0

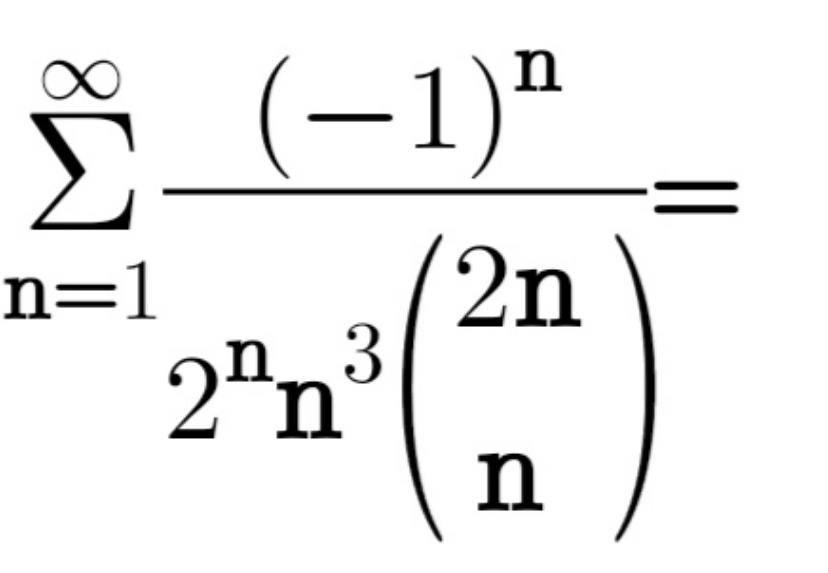
Question Number 170371 Answers: 1 Comments: 0

solve ((sin (x+18°))/(sin x)) = ((sin 18°)/(sin 12°))

$$\:{solve}\:\frac{\mathrm{sin}\:\left({x}+\mathrm{18}°\right)}{\mathrm{sin}\:{x}}\:=\:\frac{\mathrm{sin}\:\mathrm{18}°}{\mathrm{sin}\:\mathrm{12}°} \\ $$

Question Number 170369 Answers: 1 Comments: 0

Question Number 170368 Answers: 0 Comments: 0

Question Number 170352 Answers: 0 Comments: 0

Question Number 170350 Answers: 0 Comments: 0

developpement limite de ordre 3 sin^2 x et cos^2 x

$${developpement}\:{limite}\:{de}\:{ordre}\:\mathrm{3} \\ $$$${sin}^{\mathrm{2}} {x}\:\:\:\:{et}\:\:\:{cos}^{\mathrm{2}} {x} \\ $$

Question Number 170349 Answers: 1 Comments: 0

help please ∫_1 ^∞ ((1/t)−sin^(−1) ((1/t))) dt I can show that it is equal to −Σ_(n≥0) (−1)^n (((2n−1)!)/(4^n (n!)^2 (2n+1))) but I cant calculate it...

$$ \\ $$$${help}\:{please}\:\: \\ $$$$\overset{\infty} {\int}_{\mathrm{1}} \left(\frac{\mathrm{1}}{{t}}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{t}}\right)\right)\:{dt} \\ $$$${I}\:{can}\:{show}\:{that}\:{it}\:{is}\:{equal}\:{to} \\ $$$$−\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} \frac{\left(\mathrm{2}{n}−\mathrm{1}\right)!}{\mathrm{4}^{{n}} \left({n}!\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$${but}\:{I}\:{cant}\:{calculate}\:{it}... \\ $$

Question Number 170344 Answers: 1 Comments: 1

Is a semicircle a sector or a segment?

$${Is}\:{a}\:{semicircle}\:{a}\:{sector}\:{or}\:{a}\: \\ $$$${segment}? \\ $$

Question Number 170336 Answers: 2 Comments: 1

if cos^2 ∝ + 3cosec^2 θ = 7, find the expression of tan^2 θ, Hence show that tanθ=1. Mastermind

$${if}\:{cos}^{\mathrm{2}} \propto\:+\:\mathrm{3}{cosec}^{\mathrm{2}} \theta\:=\:\mathrm{7},\:{find}\:{the}\: \\ $$$${expression}\:{of}\:{tan}^{\mathrm{2}} \theta,\:{Hence}\:{show}\:{that} \\ $$$${tan}\theta=\mathrm{1}. \\ $$$$ \\ $$$${Mastermind} \\ $$

Question Number 170334 Answers: 0 Comments: 0

Question Number 170329 Answers: 1 Comments: 0

find the general solution of 1)y′′′−7y′+6y=x 2)y′′′−3y′′+2y′=(e^x /(1+e^(−x) ))

$${find}\:{the}\:{general}\:{solution}\:{of}\: \\ $$$$\left.\mathrm{1}\right){y}'''−\mathrm{7}{y}'+\mathrm{6}{y}={x} \\ $$$$\left.\mathrm{2}\right){y}'''−\mathrm{3}{y}''+\mathrm{2}{y}'=\frac{{e}^{{x}} }{\mathrm{1}+{e}^{−{x}} } \\ $$

Question Number 170327 Answers: 1 Comments: 0

Question Number 170323 Answers: 1 Comments: 0

Question Number 170322 Answers: 0 Comments: 0

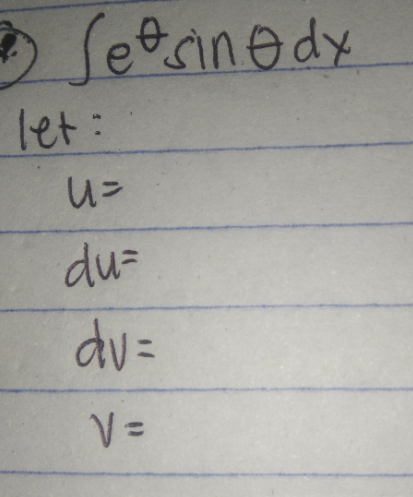
Question Number 170321 Answers: 1 Comments: 0

Question Number 170318 Answers: 0 Comments: 0

Question Number 170305 Answers: 2 Comments: 0

A number with two digits is equal to four times the sum of its digits. The number formed by reversing the order of the digit is 27 greater than the given number. Find the number

Question Number 170304 Answers: 0 Comments: 0

Question Number 170326 Answers: 0 Comments: 4

Is mass of a body greatest at the poles?. If yes or no, reason please? With diagram if possible. thanks

Question Number 170298 Answers: 0 Comments: 0

∫ (1/( ((1+x^4 ))^(1/4) ))dx

$$\int\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{1}+{x}^{\mathrm{4}} }}{dx} \\ $$

Question Number 170297 Answers: 1 Comments: 0

find the total charge enclosed inside a volume of 1.5×10^(−9) located at the origin if D=e^(−x) sin(y)a_x ^ −(e^(−x) cos(y))a_y ^ +2za^ z C/m^2

$$\:{find}\:{the}\:{total}\:{charge}\:{enclosed}\:{inside}\:{a}\: \\ $$$${volume}\:{of}\:\mathrm{1}.\mathrm{5}×\mathrm{10}^{−\mathrm{9}} \:{located}\:{at}\:{the}\:{origin} \\ $$$${if}\:{D}={e}^{−{x}} {sin}\left({y}\right)\hat {{a}}_{{x}} −\left({e}^{−{x}} {cos}\left({y}\right)\right)\hat {{a}}_{{y}} +\mathrm{2}{z}\hat {{a}z}\:{C}/{m}^{\mathrm{2}} \\ $$

Question Number 170294 Answers: 0 Comments: 0

Question Number 170292 Answers: 0 Comments: 0

Pg 487 Pg 488 Pg 489 Pg 490 Pg 491 Pg 492 Pg 493 Pg 494 Pg 495 Pg 496

Contact: info@tinkutara.com