
AllQuestion and Answers: Page 488
Question Number 171379 Answers: 0 Comments: 1
Question Number 171360 Answers: 1 Comments: 0
Question Number 171359 Answers: 1 Comments: 0
Question Number 171356 Answers: 0 Comments: 0
Question Number 171346 Answers: 0 Comments: 2
Question Number 171343 Answers: 0 Comments: 0
Question Number 171342 Answers: 1 Comments: 1

Question Number 171341 Answers: 2 Comments: 1
Question Number 171339 Answers: 1 Comments: 0
Question Number 171336 Answers: 1 Comments: 0

Question Number 171332 Answers: 0 Comments: 2
Question Number 171331 Answers: 0 Comments: 0

Question Number 176850 Answers: 1 Comments: 0
Question Number 176849 Answers: 0 Comments: 0
Question Number 176848 Answers: 1 Comments: 0
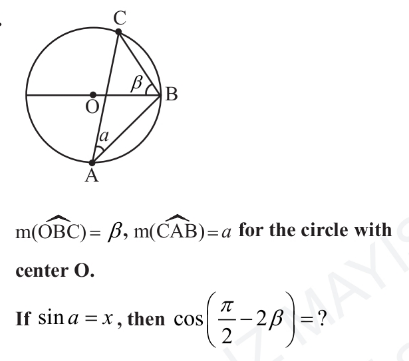
Question Number 171315 Answers: 1 Comments: 0
Question Number 171314 Answers: 1 Comments: 0
Question Number 171312 Answers: 0 Comments: 4

Question Number 171311 Answers: 0 Comments: 0
Question Number 171318 Answers: 1 Comments: 1
Question Number 171307 Answers: 1 Comments: 1
Question Number 171301 Answers: 0 Comments: 1
$$\int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{6}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3} \\ $$
Question Number 171296 Answers: 0 Comments: 1

Question Number 176853 Answers: 2 Comments: 0
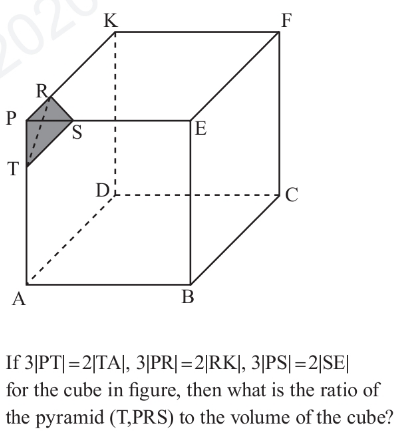
Question Number 171289 Answers: 1 Comments: 0
Question Number 171284 Answers: 2 Comments: 0
Pg 483 Pg 484 Pg 485 Pg 486 Pg 487 Pg 488 Pg 489 Pg 490 Pg 491 Pg 492
