
AllQuestion and Answers: Page 482
Question Number 171549 Answers: 1 Comments: 0
Question Number 171546 Answers: 0 Comments: 1
Question Number 171530 Answers: 0 Comments: 0

Question Number 171529 Answers: 4 Comments: 1
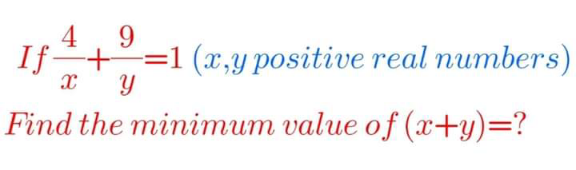
Question Number 171528 Answers: 1 Comments: 0
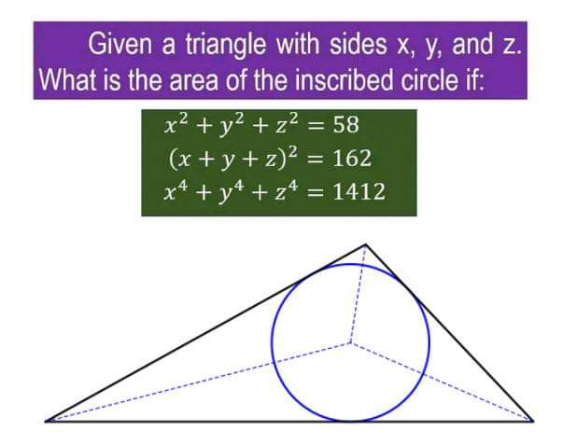
Question Number 171527 Answers: 0 Comments: 0
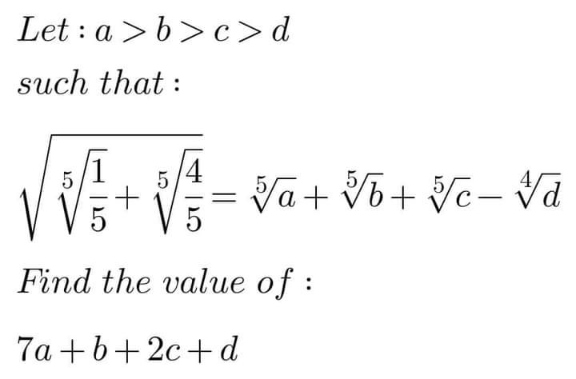
Question Number 171519 Answers: 0 Comments: 0
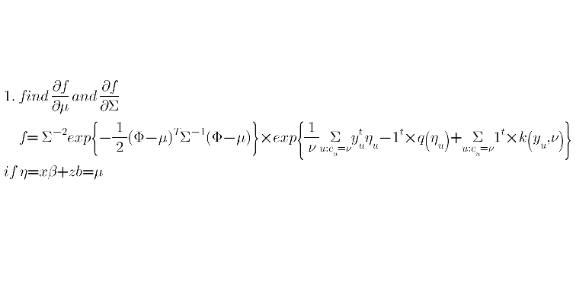
Question Number 171518 Answers: 0 Comments: 2

Question Number 176847 Answers: 3 Comments: 0
Question Number 176846 Answers: 1 Comments: 0
Question Number 171514 Answers: 0 Comments: 0
Question Number 171512 Answers: 1 Comments: 0
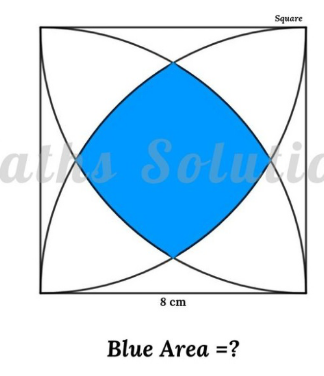
Question Number 171507 Answers: 0 Comments: 0
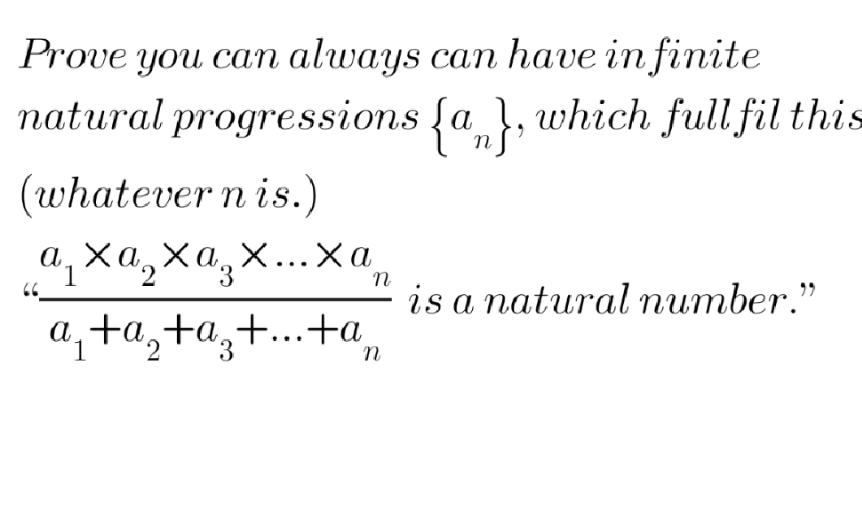
Question Number 171502 Answers: 0 Comments: 1
Question Number 171499 Answers: 1 Comments: 0
Question Number 171497 Answers: 0 Comments: 3
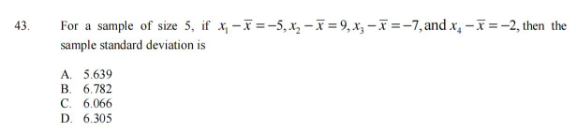
Question Number 171493 Answers: 1 Comments: 0

Question Number 171491 Answers: 0 Comments: 0
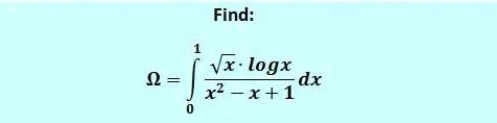
Question Number 171490 Answers: 0 Comments: 0

Question Number 171479 Answers: 1 Comments: 5
Question Number 171477 Answers: 0 Comments: 0

Question Number 171475 Answers: 1 Comments: 0

Question Number 171472 Answers: 0 Comments: 0
Question Number 171560 Answers: 1 Comments: 1
Question Number 171484 Answers: 3 Comments: 1
Question Number 171464 Answers: 0 Comments: 0
Pg 477 Pg 478 Pg 479 Pg 480 Pg 481 Pg 482 Pg 483 Pg 484 Pg 485 Pg 486
