
AllQuestion and Answers: Page 478
Question Number 172179 Answers: 0 Comments: 0

Question Number 172178 Answers: 1 Comments: 0
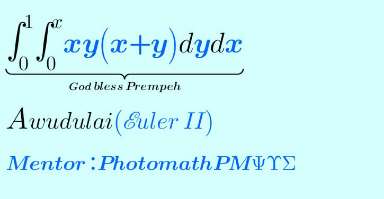
Question Number 172177 Answers: 0 Comments: 0

Question Number 172176 Answers: 1 Comments: 0
Question Number 172171 Answers: 0 Comments: 0

Question Number 172152 Answers: 1 Comments: 0

Question Number 172151 Answers: 2 Comments: 0
$$\mathrm{3}^{{x}} =\mathrm{10}−{log}_{\mathrm{2}} {x} \\ $$$${find}\:{x} \\ $$
Question Number 181360 Answers: 3 Comments: 0
Question Number 172144 Answers: 2 Comments: 0

Question Number 172124 Answers: 2 Comments: 2
Question Number 172467 Answers: 0 Comments: 0

Question Number 172111 Answers: 3 Comments: 1
Question Number 172099 Answers: 1 Comments: 0
Question Number 172089 Answers: 0 Comments: 2

Question Number 172088 Answers: 1 Comments: 0

Question Number 172084 Answers: 1 Comments: 0
Question Number 172082 Answers: 0 Comments: 1
Question Number 172081 Answers: 0 Comments: 2
Question Number 172078 Answers: 1 Comments: 0
Question Number 172077 Answers: 0 Comments: 1
Question Number 172076 Answers: 2 Comments: 0
Question Number 172085 Answers: 1 Comments: 0
Question Number 172074 Answers: 1 Comments: 0
$${solve}: \\ $$$$\mathrm{5}^{{logx}} =\mathrm{50}−{x}^{{log}\mathrm{5}} \\ $$
Question Number 172086 Answers: 1 Comments: 5
$${solve} \\ $$$$\mathrm{2}^{{x}^{\mathrm{2}} } −\mathrm{40}{x}=\mathrm{0} \\ $$
Question Number 172072 Answers: 0 Comments: 0
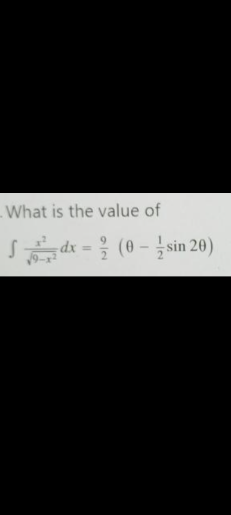
Question Number 172065 Answers: 1 Comments: 0
Pg 473 Pg 474 Pg 475 Pg 476 Pg 477 Pg 478 Pg 479 Pg 480 Pg 481 Pg 482
