Question and Answers Forum

AllQuestion and Answers: Page 474

Question Number 172323 Answers: 4 Comments: 0

which number is greater 22^(55) and 55^(22) ???

$${which}\:{number}\:{is}\:{greater} \\ $$$$\mathrm{22}^{\mathrm{55}} \:\boldsymbol{{and}}\:\mathrm{55}^{\mathrm{22}} \:??? \\ $$

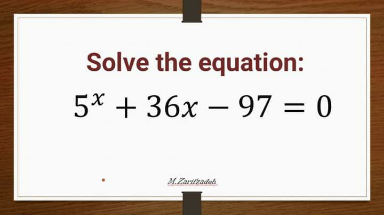
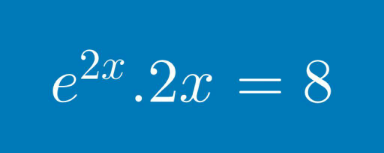
Question Number 172321 Answers: 0 Comments: 0

Question Number 172312 Answers: 1 Comments: 11

x + (2/x) = 2y y + (2/y) = 2z z + (2/z) = 2x (x, y, z) = ?

$${x}\:+\:\frac{\mathrm{2}}{{x}}\:=\:\mathrm{2}{y} \\ $$$${y}\:+\:\frac{\mathrm{2}}{{y}}\:=\:\mathrm{2}{z} \\ $$$${z}\:+\:\frac{\mathrm{2}}{{z}}\:=\:\mathrm{2}{x} \\ $$$$\left({x},\:{y},\:{z}\right)\:=\:? \\ $$

Question Number 172311 Answers: 0 Comments: 4

Using Riemann′s sum, calculate: lim b_n =(1/n)Σ_(k=0) ^(n−1) cos2(((kn)/n))

$${Using}\:{Riemann}'{s}\:{sum},\:{calculate}: \\ $$$${lim}\:{b}_{{n}} =\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {cos}\mathrm{2}\left(\frac{{kn}}{{n}}\right) \\ $$

Question Number 172309 Answers: 1 Comments: 1

Determinate lim_(n→+∞) (Σ_(k=1) ^n (((−1)^(k+1) )/k))

$${Determinate}\: \\ $$$$\underset{{n}\rightarrow+\infty} {{lim}}\left(\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{{k}}\right) \\ $$

Question Number 172307 Answers: 3 Comments: 0

Calculate lim_(n→+∞) A_n =∫_0 ^1 (x^n /(1+x))dx

$${Calculate}\: \\ $$$$\underset{{n}\rightarrow+\infty} {{lim}A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}} }{\mathrm{1}+{x}}{dx} \\ $$

Question Number 172306 Answers: 2 Comments: 0

show that J=∫_0 ^(+∞) ((ln(t))/(t^2 +a^2 ))dt with a>0 is convergent

$${show}\:{that}\:{J}=\int_{\mathrm{0}} ^{+\infty} \frac{{ln}\left({t}\right)}{{t}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dt}\:{with}\:{a}>\mathrm{0} \\ $$$${is}\:{convergent} \\ $$

Question Number 181365 Answers: 0 Comments: 0

Question Number 172304 Answers: 0 Comments: 0

study the convergence of: I(α)=∫_1 ^α (1/(t^α ((√(t^2 −1)))))dt, in function of real α. Calculate I(α) for α=1;2;4.

$${study}\:{the}\:{convergence}\:{of}: \\ $$$${I}\left(\alpha\right)=\int_{\mathrm{1}} ^{\alpha} \frac{\mathrm{1}}{{t}^{\alpha} \left(\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)}{dt},\:{in}\:{function}\: \\ $$$${of}\:{real}\:\alpha. \\ $$$${Calculate}\:{I}\left(\alpha\right)\:{for}\:\alpha=\mathrm{1};\mathrm{2};\mathrm{4}.\: \\ $$

Question Number 172287 Answers: 0 Comments: 0

Question Number 172286 Answers: 0 Comments: 0

$$ \\ $$

Question Number 172284 Answers: 1 Comments: 0

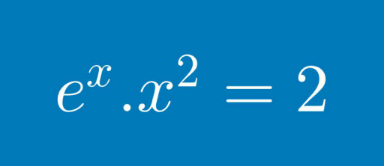
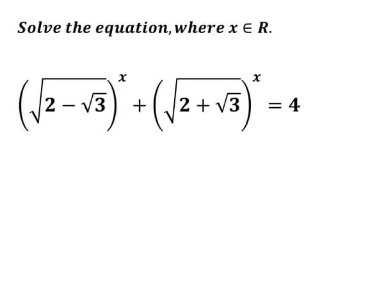
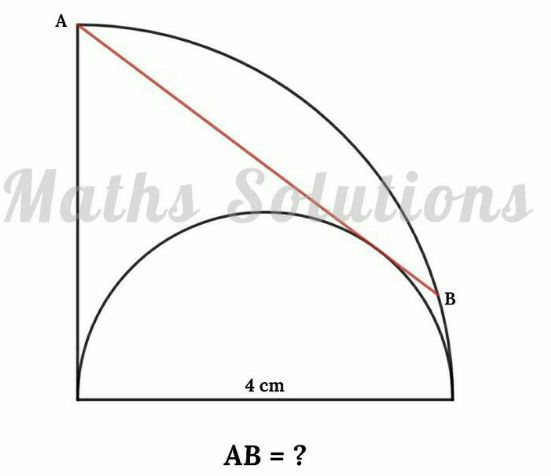
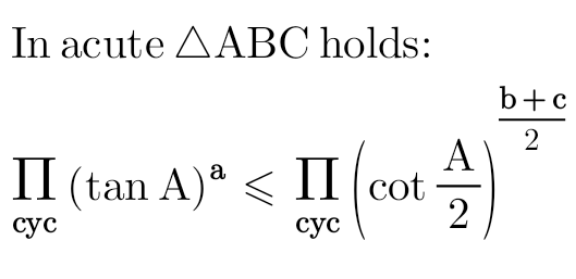
Question Number 172282 Answers: 1 Comments: 0

Find the all valid value of x x^2 − (√(4+x)) = 4

$${Find}\:{the}\:{all}\:{valid}\:{value}\:{of}\:\:\:{x} \\ $$$${x}^{\mathrm{2}} \:−\:\sqrt{\mathrm{4}+{x}}\:=\:\mathrm{4} \\ $$

Question Number 172281 Answers: 0 Comments: 0

Question Number 172269 Answers: 0 Comments: 0

A rectangular picture 6cm by 8cm is enclosed by a frame ((1/2)) wide. calculate the[area of the frame.

$${A}\:{rectangular}\:{picture}\:\mathrm{6}{cm}\:{by}\:\mathrm{8}{cm}\:{is} \\ $$$${enclosed}\:{by}\:{a}\:{frame}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:{wide}.\: \\ $$$${calculate}\:{the}\left[{area}\:{of}\:{the}\:{frame}.\right. \\ $$

Question Number 172268 Answers: 0 Comments: 0

Question Number 172267 Answers: 1 Comments: 0

Question Number 172266 Answers: 1 Comments: 0

Question Number 172265 Answers: 0 Comments: 0

Question Number 172264 Answers: 2 Comments: 0

Question Number 172263 Answers: 0 Comments: 0

Question Number 172262 Answers: 1 Comments: 0

Question Number 172261 Answers: 1 Comments: 0

Question Number 172259 Answers: 1 Comments: 0

solve x^x =3^(1/x)

$${solve} \\ $$$${x}^{{x}} =\mathrm{3}^{\frac{\mathrm{1}}{{x}}} \\ $$

Question Number 172253 Answers: 2 Comments: 0

Max and min P=(√2) x+ (√3) y subject to constraint (x^2 /9) +(y^2 /(25)) ≤ 1 ≤ x^2 +y^2

$$\:\:{Max}\:{and}\:{min}\:{P}=\sqrt{\mathrm{2}}\:{x}+\:\sqrt{\mathrm{3}}\:{y} \\ $$$${subject}\:{to}\:{constraint}\: \\ $$$$\:\frac{{x}^{\mathrm{2}} }{\mathrm{9}}\:+\frac{{y}^{\mathrm{2}} }{\mathrm{25}}\:\leqslant\:\mathrm{1}\:\leqslant\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$

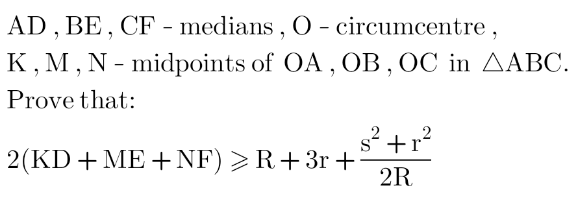
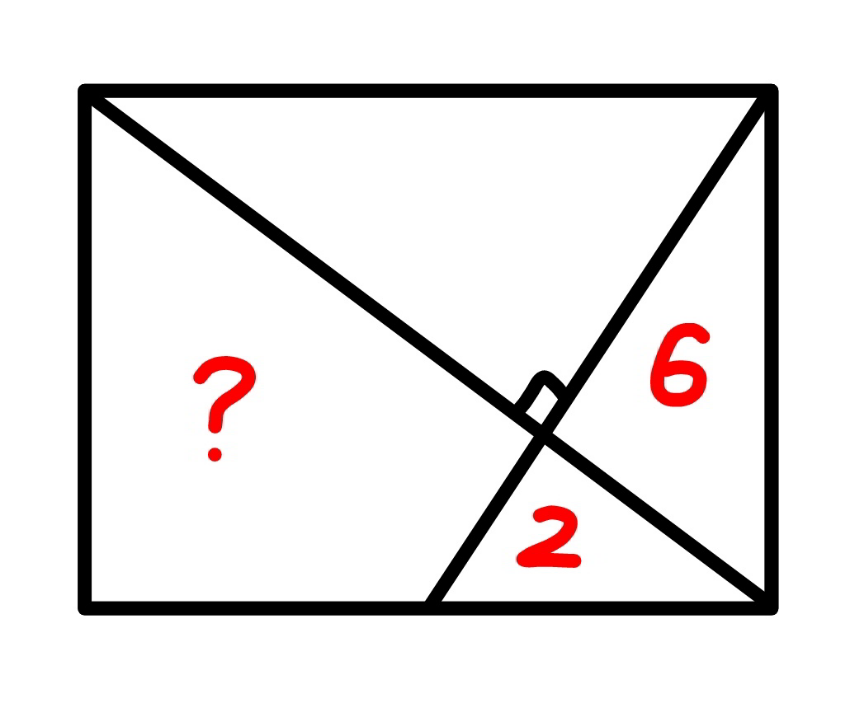
Question Number 172252 Answers: 0 Comments: 0

Pg 469 Pg 470 Pg 471 Pg 472 Pg 473 Pg 474 Pg 475 Pg 476 Pg 477 Pg 478

Contact: info@tinkutara.com