Question and Answers Forum

AllQuestion and Answers: Page 468

Question Number 171883 Answers: 0 Comments: 0

The function f(x)=ax^2 +bx+c has gradient function 4x+2 and stationary value 1. Find the values of a,b and c.

$$\mathrm{The}\:\mathrm{function}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}\:\mathrm{has}\:\mathrm{gradient} \\ $$$$\mathrm{function}\:\mathrm{4x}+\mathrm{2}\:\mathrm{and}\:\mathrm{stationary}\:\mathrm{value}\:\mathrm{1}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:{a},{b}\:\mathrm{and}\:{c}. \\ $$

Question Number 171873 Answers: 1 Comments: 2

solve: ((x+(√(x^2 −1)))/(x−(√(x^2 −1)))) −((x−(√(x^2 −1)))/(x+(√(x^2 −1)))) =8x(√(x^2 −3x+2))

$${solve}: \\ $$$$\frac{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:−\frac{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:\:=\mathrm{8}{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}} \\ $$

Question Number 171872 Answers: 1 Comments: 0

Solve for real numbers: (1/(1 + tan^4 x)) + (1/(10)) = (2/(1 + 3 tan^2 x))

$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{tan}^{\mathrm{4}} \:\mathrm{x}}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{10}}\:\:=\:\:\frac{\mathrm{2}}{\mathrm{1}\:+\:\mathrm{3}\:\mathrm{tan}^{\mathrm{2}} \:\mathrm{x}} \\ $$

Question Number 171871 Answers: 1 Comments: 2

solve: ((x+(√(x^2 −1)))/(x−(√(x^2 −1)))) + ((x−(√(x^2 −1)))/(x+(√(x^2 −1)))) =98

$${solve}: \\ $$$$\frac{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:\:+\:\:\frac{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\mathrm{98} \\ $$

Question Number 171870 Answers: 1 Comments: 0

if x is a real number,then (√(log_e ((4x−x^2 )/3) ))

$${if}\:{x}\:{is}\:{a}\:{real}\:{number},{then} \\ $$$$\sqrt{{log}_{{e}} \:\frac{\mathrm{4}{x}−{x}^{\mathrm{2}} }{\mathrm{3}}\:}\:\: \\ $$

Question Number 171869 Answers: 2 Comments: 0

find the square root of: (√((7x^2 +2(√(14)) x+2)/(x^2 −(1/2)x +(1/6))))

$${find}\:{the}\:{square}\:{root}\:{of}: \\ $$$$\sqrt{\frac{\mathrm{7}{x}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{14}}\:{x}+\mathrm{2}}{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{x}\:+\frac{\mathrm{1}}{\mathrm{6}}}} \\ $$

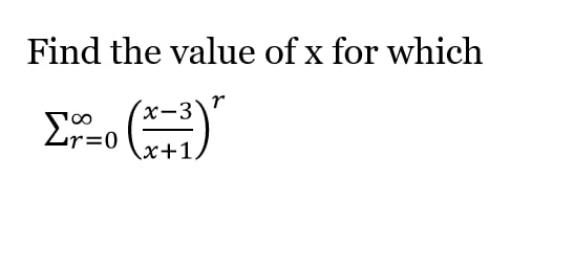
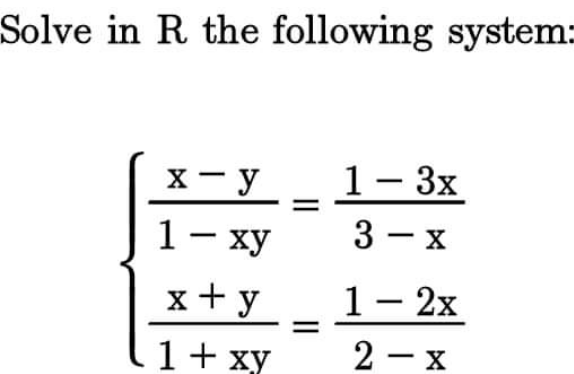
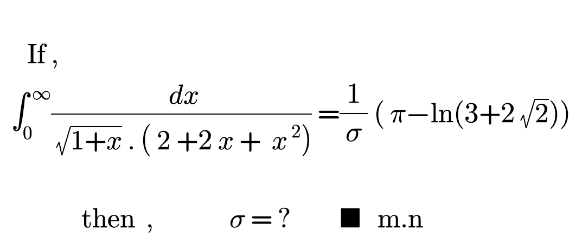
Question Number 171868 Answers: 0 Comments: 2

solve: x^2 +y^2 =1997(x−y),find the positive integer solution.

$${solve}: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1997}\left({x}−{y}\right),{find}\:{the}\:{positive}\:{integer}\:{solution}. \\ $$

Question Number 171867 Answers: 1 Comments: 0

solve: x_4 ^2 =100100_2 , find x and leave answer in base 2.

$${solve}:\:{x}_{\mathrm{4}} ^{\mathrm{2}} =\mathrm{100100}_{\mathrm{2}} ,\:{find}\:{x}\:{and}\:{leave}\:{answer}\:{in}\:{base}\:\mathrm{2}. \\ $$

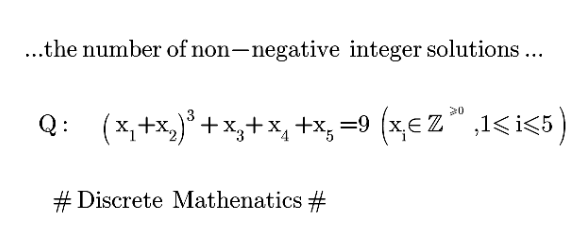
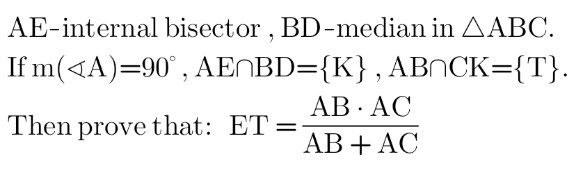
Question Number 171866 Answers: 0 Comments: 1

(√a)+(√b)=(√(2009)). find a and b.

$$\sqrt{{a}}+\sqrt{{b}}=\sqrt{\mathrm{2009}}.\:{find}\:{a}\:{and}\:{b}. \\ $$

Question Number 171861 Answers: 0 Comments: 8

if ax+by=5 ax^2 +by^2 =10 ax^3 +by^3 =50 ax^4 +by^4 =130 find 13(x+y−xy)−120(a+b)

$${if}\: \\ $$$${ax}+{by}=\mathrm{5} \\ $$$${ax}^{\mathrm{2}} +{by}^{\mathrm{2}} =\mathrm{10} \\ $$$${ax}^{\mathrm{3}} +{by}^{\mathrm{3}} =\mathrm{50} \\ $$$${ax}^{\mathrm{4}} +{by}^{\mathrm{4}} =\mathrm{130} \\ $$$${find}\:\mathrm{13}\left({x}+{y}−{xy}\right)−\mathrm{120}\left({a}+{b}\right) \\ $$

Question Number 171860 Answers: 0 Comments: 0

solve: ((4x^2 )/([1−(√(1+2x))]^2 ))<2x+9

$${solve}: \\ $$$$\frac{\mathrm{4}{x}^{\mathrm{2}} }{\left[\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{2}{x}}\right]^{\mathrm{2}} }<\mathrm{2}{x}+\mathrm{9} \\ $$

Question Number 171858 Answers: 0 Comments: 0

solve: find the value of x and y between 0^(° ) and180^° which satisfy the simultaneous eqn sin(x+y)=((√2)/2) cos2x=−(1/2)

$${solve}: \\ $$$${find}\:{the}\:{value}\:{of}\:{x}\:{and}\:{y}\:{between}\:\mathrm{0}^{°\:} {and}\mathrm{180}^{°} \:{which}\:{satisfy}\:{the}\:{simultaneous}\:{eqn} \\ $$$${sin}\left({x}+{y}\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${cos}\mathrm{2}{x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$

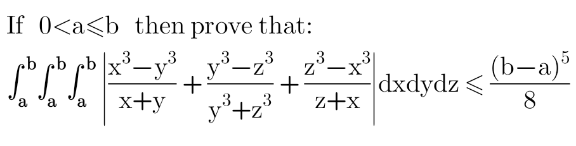
Question Number 171854 Answers: 1 Comments: 0

solve: (3(√2))^n =3

$${solve}: \\ $$$$\left(\mathrm{3}\sqrt{\mathrm{2}}\right)^{{n}} =\mathrm{3} \\ $$

Question Number 171849 Answers: 1 Comments: 1

solve: 3^(2x+y) =12 2^(x−y) =4

$${solve}: \\ $$$$\mathrm{3}^{\mathrm{2}{x}+{y}} =\mathrm{12} \\ $$$$\mathrm{2}^{{x}−{y}} =\mathrm{4} \\ $$

Question Number 171847 Answers: 1 Comments: 1

solve: log_x 10+log_x^2 10=6

$${solve}: \\ $$$${log}_{{x}} \mathrm{10}+{log}_{{x}^{\mathrm{2}} } \mathrm{10}=\mathrm{6} \\ $$

Question Number 171846 Answers: 0 Comments: 2

solve: x^9 −2x^5 −3x=0

$${solve}: \\ $$$${x}^{\mathrm{9}} −\mathrm{2}{x}^{\mathrm{5}} −\mathrm{3}{x}=\mathrm{0} \\ $$

Question Number 171845 Answers: 0 Comments: 0

n_c_(r+1) + n_c_r =n+1_c_(r .solve for n and r.)

$${n}_{{c}_{{r}+\mathrm{1}} } +\:{n}_{{c}_{{r}} } ={n}+\mathrm{1}_{{c}_{{r}\:\:.{solve}\:{for}\:\:{n}\:{and}\:{r}.} } \\ $$

Question Number 171844 Answers: 1 Comments: 0

solve: x^5 −5x^4 +9x^3 −9x^2 +5x−1=0

$${solve}: \\ $$$${x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{4}} +\mathrm{9}{x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{1}=\mathrm{0} \\ $$

Question Number 171843 Answers: 0 Comments: 0

find a: (2:3:4:5)a=5:6:7:8

$${find}\:{a}: \\ $$$$\left(\mathrm{2}:\mathrm{3}:\mathrm{4}:\mathrm{5}\right){a}=\mathrm{5}:\mathrm{6}:\mathrm{7}:\mathrm{8} \\ $$

Question Number 171841 Answers: 1 Comments: 0

solve: 2^((5x−20)) =1!

$${solve}: \\ $$$$\mathrm{2}^{\left(\mathrm{5}{x}−\mathrm{20}\right)} =\mathrm{1}! \\ $$

Question Number 171840 Answers: 0 Comments: 0

solve: a^3 +9ab^2 =26 a^2 b+ab^3 =15

$${solve}: \\ $$$${a}^{\mathrm{3}} +\mathrm{9}{ab}^{\mathrm{2}} =\mathrm{26} \\ $$$${a}^{\mathrm{2}} {b}+{ab}^{\mathrm{3}} =\mathrm{15} \\ $$

Question Number 171839 Answers: 0 Comments: 0

solve the simultaneous eqn y=ax^2 +bx+c y=b_1 x+c_1

$${solve}\:{the}\:{simultaneous}\:{eqn} \\ $$$${y}={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${y}={b}_{\mathrm{1}} {x}+{c}_{\mathrm{1}} \\ $$

Question Number 171838 Answers: 0 Comments: 0

solve: 4^x^2 +3x=6

$${solve}: \\ $$$$\mathrm{4}^{{x}^{\mathrm{2}} } +\mathrm{3}{x}=\mathrm{6} \\ $$

Question Number 171837 Answers: 1 Comments: 0

solve: 2x+3y=2 x+y=5xy

$${solve}: \\ $$$$\mathrm{2}{x}+\mathrm{3}{y}=\mathrm{2} \\ $$$${x}+{y}=\mathrm{5}{xy} \\ $$

Question Number 171836 Answers: 1 Comments: 0

solve: x+3y=1 xy=y^2 −3

$${solve}: \\ $$$${x}+\mathrm{3}{y}=\mathrm{1} \\ $$$${xy}={y}^{\mathrm{2}} −\mathrm{3} \\ $$

Question Number 171835 Answers: 1 Comments: 0

solve for x: x^5 +x^4 +1=0

$${solve}\:{for}\:{x}: \\ $$$${x}^{\mathrm{5}} +{x}^{\mathrm{4}} +\mathrm{1}=\mathrm{0} \\ $$

Pg 463 Pg 464 Pg 465 Pg 466 Pg 467 Pg 468 Pg 469 Pg 470 Pg 471 Pg 472

Contact: info@tinkutara.com