Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 465

Question Number 172181 Answers: 0 Comments: 0

Question Number 172180 Answers: 0 Comments: 0

Question Number 172179 Answers: 0 Comments: 0

Question Number 172178 Answers: 1 Comments: 0

Question Number 172177 Answers: 0 Comments: 0

Question Number 172176 Answers: 1 Comments: 0

solve: 2^n +n=4

$${solve}: \\ $$$$\mathrm{2}^{{n}} +{n}=\mathrm{4} \\ $$

Question Number 172171 Answers: 0 Comments: 0

Question Number 172152 Answers: 1 Comments: 0

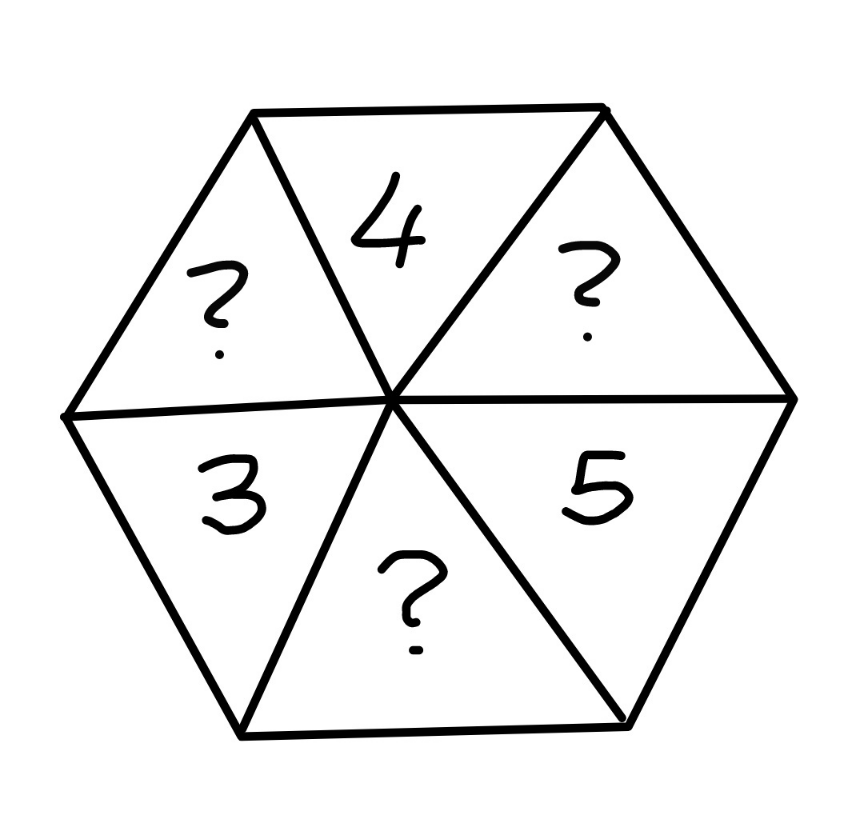
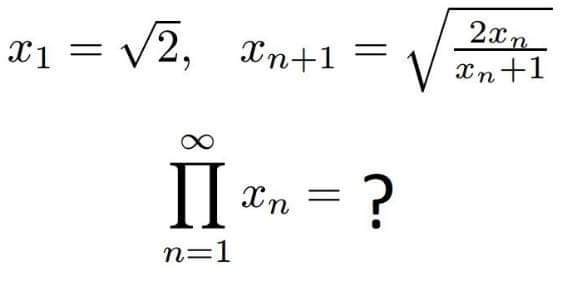
Question Number 172151 Answers: 2 Comments: 0

3^x =10−log_2 x find x

$$\mathrm{3}^{{x}} =\mathrm{10}−{log}_{\mathrm{2}} {x} \\ $$$${find}\:{x} \\ $$

Question Number 181360 Answers: 3 Comments: 0

Calcul Σ_(k=0) ^n k((1/3))^k =...

$${Calcul} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{k}} =... \\ $$

Question Number 172144 Answers: 2 Comments: 0

Question Number 172124 Answers: 2 Comments: 2

if tanθ+secθ=x, show that sinθ=((x^2 −1)/(x^2 +1))

$${if}\:{tan}\theta+{sec}\theta={x},\:{show}\:{that}\: \\ $$$${sin}\theta=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$

Question Number 172467 Answers: 0 Comments: 0

Question Number 172111 Answers: 3 Comments: 1

solve 2^x =4x

$${solve} \\ $$$$\mathrm{2}^{{x}} =\mathrm{4}{x} \\ $$

Question Number 172099 Answers: 1 Comments: 0

The probability that Abiola will be late to office on a given day is(2/5) . in a given week of six days, find the 1) probability that he will be late of only 3 days 2) not be late in the week

$${The}\:{probability}\:{that}\:{Abiola}\:{will}\:{be} \\ $$$${late}\:{to}\:{office}\:{on}\:{a}\:{given}\:{day}\:{is}\frac{\mathrm{2}}{\mathrm{5}}\:.\:{in} \\ $$$${a}\:{given}\:{week}\:{of}\:{six}\:{days},\:{find}\:{the}\: \\ $$$$\left.\mathrm{1}\right)\:{probability}\:{that}\:{he}\:{will}\:{be}\:{late}\:{of} \\ $$$${only}\:\mathrm{3}\:{days} \\ $$$$\left.\mathrm{2}\right)\:{not}\:{be}\:{late}\:{in}\:{the}\:{week} \\ $$

Question Number 172089 Answers: 0 Comments: 2

Question Number 172088 Answers: 1 Comments: 0

Question Number 172084 Answers: 1 Comments: 0

solve ((√(5+(√(24)))))^x −10=((√(5−(√(24)))))^x

$${solve} \\ $$$$\left(\sqrt{\mathrm{5}+\sqrt{\mathrm{24}}}\right)^{{x}} −\mathrm{10}=\left(\sqrt{\mathrm{5}−\sqrt{\mathrm{24}}}\right)^{{x}} \\ $$

Question Number 172082 Answers: 0 Comments: 1

solve log_(0.5) ^2 x+log_(0.5) x−2<_− 0

$${solve} \\ $$$${log}_{\mathrm{0}.\mathrm{5}} ^{\mathrm{2}} {x}+{log}_{\mathrm{0}.\mathrm{5}} {x}−\mathrm{2}\underset{−} {<}\mathrm{0} \\ $$

Question Number 172081 Answers: 0 Comments: 2

solve log_(1/3) (5x−1)>_− 0

$${solve} \\ $$$${log}_{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{5}{x}−\mathrm{1}\right)\underset{−} {>}\mathrm{0} \\ $$

Question Number 172078 Answers: 1 Comments: 0

solve ((2logx)/(log(5x−4)))=1

$${solve} \\ $$$$\frac{\mathrm{2}{logx}}{{log}\left(\mathrm{5}{x}−\mathrm{4}\right)}=\mathrm{1} \\ $$

Question Number 172077 Answers: 0 Comments: 1

solve log_4 (x+12).logx^2 =1

$${solve} \\ $$$${log}_{\mathrm{4}} \left({x}+\mathrm{12}\right).{logx}^{\mathrm{2}} =\mathrm{1} \\ $$

Question Number 172076 Answers: 2 Comments: 0

solve log(64(2^(x^2 −40x) )^(1/(24)) )=0

$${solve} \\ $$$${log}\left(\mathrm{64}\sqrt[{\mathrm{24}}]{\mathrm{2}^{{x}^{\mathrm{2}} −\mathrm{40}{x}} }\right)=\mathrm{0} \\ $$

Question Number 172085 Answers: 1 Comments: 0

solve (3^(x^3 −72x+39) −9(√3))×log(7−x)=0

$${solve} \\ $$$$\left(\mathrm{3}^{{x}^{\mathrm{3}} −\mathrm{72}{x}+\mathrm{39}} −\mathrm{9}\sqrt{\mathrm{3}}\right)×{log}\left(\mathrm{7}−{x}\right)=\mathrm{0} \\ $$

Question Number 172074 Answers: 1 Comments: 0

solve: 5^(logx) =50−x^(log5)

$${solve}: \\ $$$$\mathrm{5}^{{logx}} =\mathrm{50}−{x}^{{log}\mathrm{5}} \\ $$

Question Number 172086 Answers: 1 Comments: 5

solve 2^x^2 −40x=0

$${solve} \\ $$$$\mathrm{2}^{{x}^{\mathrm{2}} } −\mathrm{40}{x}=\mathrm{0} \\ $$

Pg 460 Pg 461 Pg 462 Pg 463 Pg 464 Pg 465 Pg 466 Pg 467 Pg 468 Pg 469

Contact: info@tinkutara.com