Question and Answers Forum

AllQuestion and Answers: Page 459

Question Number 174143 Answers: 2 Comments: 5

If 4^x = 5^y = 3^z find (a/b) + (a/c) Answer: (1;2)

$$\mathrm{If}\:\:\mathrm{4}^{\boldsymbol{\mathrm{x}}} \:=\:\mathrm{5}^{\boldsymbol{\mathrm{y}}} \:=\:\mathrm{3}^{\boldsymbol{\mathrm{z}}} \:\:\mathrm{find}\:\:\frac{\mathrm{a}}{\mathrm{b}}\:+\:\frac{\mathrm{a}}{\mathrm{c}} \\ $$$$\mathrm{Answer}:\:\:\left(\mathrm{1};\mathrm{2}\right) \\ $$

Question Number 174133 Answers: 0 Comments: 2

Question Number 174131 Answers: 0 Comments: 3

Question Number 174127 Answers: 1 Comments: 0

Q: p , q , r are roots of x^( 3) −7x^( 2) =(4−x)(x+2) find the value of : K = (1/( ((qr))^(1/3) )) + (1/( ((pr))^(1/3) )) + (1/( ((pq))^(1/3) )) = ?

$$ \\ $$$$\:\:\:{Q}:\:\:\:\:\:{p}\:,\:{q}\:,\:{r}\:\:\:\:{are}\:\:{roots}\:{of} \\ $$$$\:\:\:\:\:{x}^{\:\mathrm{3}} \:−\mathrm{7}{x}^{\:\mathrm{2}} =\left(\mathrm{4}−{x}\right)\left({x}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:{find}\:\:{the}\:{value}\:{of}\:: \\ $$$$\:\:\:\mathrm{K}\:=\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{qr}}}\:\:+\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{pr}}}\:\:+\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{pq}}}\:=\:? \\ $$$$ \\ $$

Question Number 174124 Answers: 0 Comments: 7

C3^n −4C^(3n−1) =3^n find C for any n

$${C}\mathrm{3}^{{n}} −\mathrm{4}{C}^{\mathrm{3}{n}−\mathrm{1}} =\mathrm{3}^{{n}} \\ $$$${find}\:{C}\:\:{for}\:{any}\:{n}\: \\ $$

Question Number 174118 Answers: 1 Comments: 0

calculate Σ_(n=1) ^∞ (((−1)^n )/n) by using ψ (digamma)

$${calculate}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:{by}\:{using} \\ $$$$\psi\:\:\left({digamma}\right) \\ $$

Question Number 174117 Answers: 1 Comments: 0

find ∫_0 ^1 (dx/(1+x^n )) interms of ψ (digamma)

$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{1}+{x}^{{n}} }\:{interms}\:{of} \\ $$$$\psi\:\left({digamma}\right) \\ $$

Question Number 181440 Answers: 0 Comments: 0

Question Number 181439 Answers: 1 Comments: 0

Question Number 181438 Answers: 2 Comments: 1

If a + (1/b) = b + (1/c) = c + (1/a) then prove that abc = ±1. a ≠ b ≠ c

$$\mathrm{If}\:{a}\:+\:\frac{\mathrm{1}}{{b}}\:=\:{b}\:+\:\frac{\mathrm{1}}{{c}}\:=\:{c}\:+\:\frac{\mathrm{1}}{{a}}\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$${abc}\:=\:\pm\mathrm{1}.\:\:\:{a}\:\neq\:{b}\:\neq\:{c} \\ $$

Question Number 181437 Answers: 2 Comments: 0

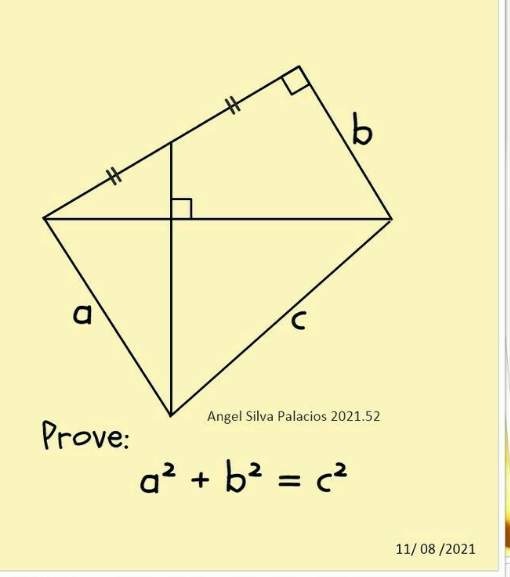
Question Number 181435 Answers: 0 Comments: 0

((𝛅^2 u)/(𝛅t^2 )) = 4 ((𝛅^2 u)/(𝛅x^2 )) ; u∣_(t=0) =sin(x) ; ((𝛅u)/(𝛅t))∣_(t=0) =x

$$\:\:\:\frac{\boldsymbol{\delta}^{\mathrm{2}} \boldsymbol{\mathrm{u}}}{\boldsymbol{\delta\mathrm{t}}^{\mathrm{2}} }\:=\:\mathrm{4}\:\frac{\boldsymbol{\delta}^{\mathrm{2}} \boldsymbol{\mathrm{u}}}{\boldsymbol{\delta\mathrm{x}}^{\mathrm{2}} }\:\:\:;\:\:\boldsymbol{\mathrm{u}}\mid_{\boldsymbol{\mathrm{t}}=\mathrm{0}} =\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)\:\:\:;\:\:\:\frac{\boldsymbol{\delta\mathrm{u}}}{\boldsymbol{\delta\mathrm{t}}}\mid_{\boldsymbol{\mathrm{t}}=\mathrm{0}} =\boldsymbol{\mathrm{x}} \\ $$

Question Number 181432 Answers: 1 Comments: 5

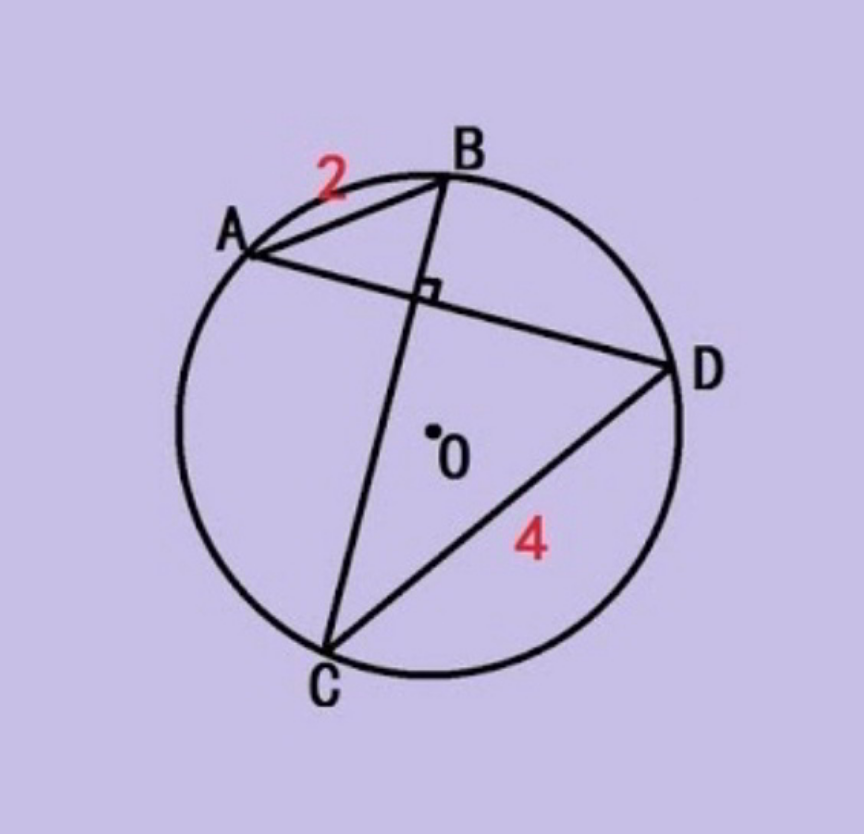
Question Number 174096 Answers: 2 Comments: 0

f(x)= ax^( 2) + bx +c is given a ≠ b ≠ c , a , b , c ∈ R a≠0 and : f(ax + b )=f (bx + c) find : (1/2) (f(b) − f(a ))=?

$$ \\ $$$$\:\:\:{f}\left({x}\right)=\:{ax}^{\:\mathrm{2}} +\:{bx}\:+{c}\:\:{is}\:{given} \\ $$$$\:\:\:\:\:\:{a}\:\neq\:{b}\:\neq\:{c}\:\:,\:{a}\:,\:{b}\:,\:{c}\:\in\:\mathbb{R}\: \\ $$$$\:\:\:\:\:\:\:{a}\neq\mathrm{0}\:\:\:{and}\:\:\:: \\ $$$$\:\:\:\:\:\:\:\:{f}\left({ax}\:+\:{b}\:\right)={f}\:\left({bx}\:+\:{c}\right) \\ $$$$\:\:\:\:\:\:{find}\::\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\left({f}\left({b}\right)\:\:−\:{f}\left({a}\:\right)\right)=? \\ $$

Question Number 174094 Answers: 1 Comments: 0

The circles x^2 +y^2 −2ax+8y+13=0 and x^2 +y^2 +2x+2by+1=0 are congruent. If they are 2(√(10)) units apart, find the possible values of a and b.

$$\mathrm{The}\:\mathrm{circles}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{ax}+\mathrm{8}{y}+\mathrm{13}=\mathrm{0} \\ $$$$\mathrm{and}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}{by}+\mathrm{1}=\mathrm{0}\:\mathrm{are}\: \\ $$$$\mathrm{congruent}.\:\mathrm{If}\:\mathrm{they}\:\mathrm{are}\:\mathrm{2}\sqrt{\mathrm{10}}\:\mathrm{units}\: \\ $$$$\mathrm{apart},\:\mathrm{find}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{of} \\ $$$${a}\:\mathrm{and}\:{b}. \\ $$

Question Number 174095 Answers: 0 Comments: 0

prove the distance between object and image of glass slab.

$${prove}\:{the}\:{distance}\:{between}\:{object}\:{and} \\ $$$${image}\:{of}\:{glass}\:{slab}. \\ $$

Question Number 174084 Answers: 2 Comments: 1

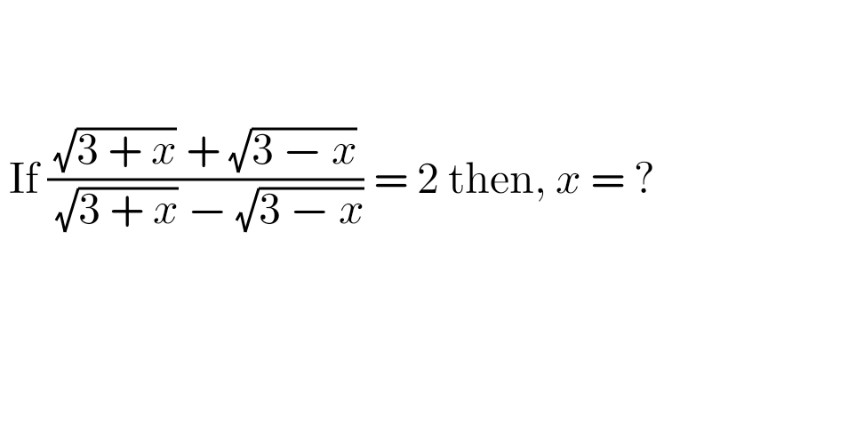
Question Number 174074 Answers: 1 Comments: 1

Question Number 174071 Answers: 2 Comments: 0

Question Number 174069 Answers: 1 Comments: 1

Question Number 174092 Answers: 2 Comments: 0

x^4 +ax^2 +14x−210=0 x_1 .x_2 =22, a=?

$$\:\:\:\:\:\:\boldsymbol{{x}}^{\mathrm{4}} +\boldsymbol{{ax}}^{\mathrm{2}} +\mathrm{14}\boldsymbol{{x}}−\mathrm{210}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{{x}}_{\mathrm{1}} .\boldsymbol{{x}}_{\mathrm{2}} =\mathrm{22},\:\:\:\:\:\:\:\boldsymbol{{a}}=? \\ $$

Question Number 174062 Answers: 2 Comments: 3

find all prime p and q such that p^2 − p = 37q^2 − q

$$\mathrm{find}\:\mathrm{all}\:\mathrm{prime}\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}\:\:\mathrm{such}\:\mathrm{that}\:\:\:\:\mathrm{p}^{\mathrm{2}} \:\:−\:\:\mathrm{p}\:\:\:\:=\:\:\:\mathrm{37q}^{\mathrm{2}} \:\:−\:\:\mathrm{q} \\ $$

Question Number 174059 Answers: 2 Comments: 3

if x^3 +y^3 +3xy=1, then x+y=?

$${if}\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +\mathrm{3}{xy}=\mathrm{1},\:{then}\:{x}+{y}=? \\ $$

Question Number 174057 Answers: 0 Comments: 1

Question Number 174056 Answers: 0 Comments: 0

Question Number 174036 Answers: 1 Comments: 0

Factorize x^2 + (√(2x ))+ x + 2

$$\:\:\mathrm{Factorize}\:{x}^{\mathrm{2}} \:+\:\sqrt{\mathrm{2}{x}\:}+\:{x}\:+\:\mathrm{2} \\ $$

Pg 454 Pg 455 Pg 456 Pg 457 Pg 458 Pg 459 Pg 460 Pg 461 Pg 462 Pg 463

Contact: [email protected]