Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 454

Question Number 172821 Answers: 0 Comments: 1

Question Number 172820 Answers: 1 Comments: 0

Question Number 172819 Answers: 3 Comments: 0

Question Number 172818 Answers: 1 Comments: 0

Question Number 172817 Answers: 2 Comments: 0

Question Number 172816 Answers: 0 Comments: 0

Question Number 172802 Answers: 1 Comments: 0

Q: how many natural numbers less than 6000 , exist such as the sum of their digits equal to 8 ? choices: 155 165 164 158

$$ \\ $$$$\:\:\:\: \\ $$$$\:\mathrm{Q}:\:\:\:\:\mathrm{how}\:\mathrm{many}\:\mathrm{natural}\:\mathrm{numbers}\:\mathrm{less}\:\mathrm{than} \\ $$$$\:\:\:\:\:\:\mathrm{6000}\:\:,\:\mathrm{exist}\:\mathrm{such}\:\mathrm{as}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{their}\:\mathrm{digits}\:\:\mathrm{equal}\:\mathrm{to}\:\:\:\mathrm{8}\:? \\ $$$$\:\mathrm{choices}:\:\:\:\:\mathrm{155}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{165}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{164}\:\:\:\:\:\:\:\:\:\:\mathrm{158} \\ $$$$\:\:\:\:\:\:\: \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Question Number 172798 Answers: 1 Comments: 0

a^( 2) −1 ≡^(10) 14a +6 a^( 2) +a ≡^(10) ? choices: 2 3 7 8

$$ \\ $$$$\:\:\:\:\:\mathrm{a}^{\:\mathrm{2}} −\mathrm{1}\:\overset{\mathrm{10}} {\equiv}\:\mathrm{14a}\:+\mathrm{6} \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\:\mathrm{2}} \:+\mathrm{a}\:\overset{\mathrm{10}} {\equiv}\:?\:\:\:\: \\ $$$$\:\:\mathrm{choices}:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{7}\:\:\:\:\:\:\:\:\:\:\:\mathrm{8} \\ $$$$\: \\ $$$$ \\ $$$$ \\ $$

Question Number 172787 Answers: 0 Comments: 0

In AB^Δ C , prove that sin((A/2)).sin((B/2)).sin((C/2)) ≤ (1/8) −−−−−−−−

$$ \\ $$$$\:\:\:\mathrm{In}\:\:\mathrm{A}\overset{\Delta} {\mathrm{B}C}\:\:,\:\mathrm{prove}\:\:\mathrm{that}\: \\ $$$$\:{sin}\left(\frac{\mathrm{A}}{\mathrm{2}}\right).{sin}\left(\frac{\mathrm{B}}{\mathrm{2}}\right).{sin}\left(\frac{\mathrm{C}}{\mathrm{2}}\right)\:\leqslant\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\:\:\:−−−−−−−− \\ $$$$ \\ $$

Question Number 172785 Answers: 1 Comments: 0

Question Number 172784 Answers: 1 Comments: 0

Question Number 172775 Answers: 2 Comments: 0

Question Number 172770 Answers: 0 Comments: 0

Question Number 172767 Answers: 0 Comments: 2

Φ=∫_0 ^1 ((((−1)^(1/x) )/x))dx=?

$$\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{{x}}} }{{x}}\right){dx}=? \\ $$

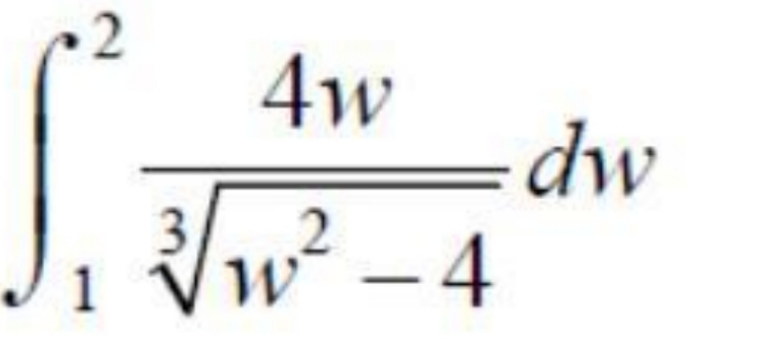
Question Number 172766 Answers: 0 Comments: 0

lim_(x→0) ((x!!−(√(2/π)))/(((1/1^2 )+(1/2^2 )+(1/3^3 )+∙∙∙)−Ψ_1 (x+1)))=? solve this pleas

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}!!−\sqrt{\frac{\mathrm{2}}{\pi}}}{\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }+\centerdot\centerdot\centerdot\right)−\Psi_{\mathrm{1}} \left({x}+\mathrm{1}\right)}=? \\ $$$${solve}\:{this}\:{pleas} \\ $$

Question Number 172764 Answers: 1 Comments: 0

∫_0 ^∞ (((ln(1−x))/x))^2 dx= ?

$$\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\right)^{\mathrm{2}} \:\mathrm{dx}=\:? \\ $$

Question Number 172763 Answers: 2 Comments: 0

Question Number 172762 Answers: 1 Comments: 0

Question Number 172758 Answers: 0 Comments: 0

Question Number 172756 Answers: 0 Comments: 12

Question Number 172749 Answers: 4 Comments: 3

Question Number 172744 Answers: 1 Comments: 0

Question Number 172741 Answers: 1 Comments: 0

∫_0 ^π Sin ^(100) xdx

$$\underset{\mathrm{0}} {\overset{\pi} {\int}}{Sin}\overset{\mathrm{100}} {\:}{xdx} \\ $$

Question Number 172740 Answers: 1 Comments: 1

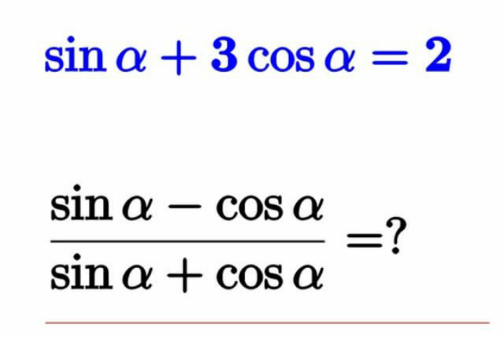
Question Number 172732 Answers: 2 Comments: 0

sinθ−cosθ=(1/2) sin^4 θ+cos^4 θ=?

$$\mathrm{sin}\theta−\mathrm{cos}\theta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \theta=? \\ $$

Question Number 172731 Answers: 0 Comments: 0

Pg 449 Pg 450 Pg 451 Pg 452 Pg 453 Pg 454 Pg 455 Pg 456 Pg 457 Pg 458

Terms of Service

Contact: info@tinkutara.com