
AllQuestion and Answers: Page 447
Question Number 175285 Answers: 2 Comments: 0
Question Number 175284 Answers: 1 Comments: 0

Question Number 175280 Answers: 2 Comments: 0
Question Number 175277 Answers: 0 Comments: 0

Question Number 175279 Answers: 3 Comments: 0
Question Number 175275 Answers: 1 Comments: 0
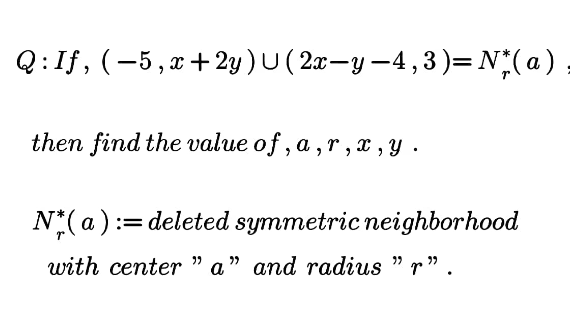
Question Number 181521 Answers: 2 Comments: 0
Question Number 175266 Answers: 0 Comments: 1
Question Number 175265 Answers: 1 Comments: 0
Question Number 175264 Answers: 1 Comments: 0

Question Number 175251 Answers: 1 Comments: 0
Question Number 175250 Answers: 0 Comments: 0
Question Number 175247 Answers: 2 Comments: 0

Question Number 175244 Answers: 1 Comments: 0
Question Number 175237 Answers: 0 Comments: 0
Question Number 181485 Answers: 2 Comments: 0
Question Number 181484 Answers: 0 Comments: 6
Question Number 175240 Answers: 1 Comments: 1

Question Number 175230 Answers: 1 Comments: 0

Question Number 175221 Answers: 2 Comments: 0

Question Number 175218 Answers: 1 Comments: 0
Question Number 175217 Answers: 0 Comments: 1
Question Number 175213 Answers: 2 Comments: 0
Question Number 175211 Answers: 1 Comments: 0
Question Number 175210 Answers: 0 Comments: 0
Question Number 175199 Answers: 1 Comments: 0
Pg 442 Pg 443 Pg 444 Pg 445 Pg 446 Pg 447 Pg 448 Pg 449 Pg 450 Pg 451
