Question and Answers Forum

AllQuestion and Answers: Page 445

Question Number 174404 Answers: 1 Comments: 0

Question Number 174396 Answers: 2 Comments: 0

Question Number 174389 Answers: 1 Comments: 0

what is least upper bound of the sequence {(1+(1/n))ln(1+(1/n))}_(n=1) ^∞ ? A.0 B.ln2 C.ln5 D.2ln2

$${what}\:{is}\:\:{least}\:{upper}\:{bound}\:{of}\:{the} \\ $$$${sequence}\:\left\{\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\right\}_{{n}=\mathrm{1}} ^{\infty} ? \\ $$$${A}.\mathrm{0}\:\:\:\:{B}.{ln}\mathrm{2}\:\:\:\:\:\:{C}.{ln}\mathrm{5}\:\:\:\:\:\:\:{D}.\mathrm{2}{ln}\mathrm{2}\: \\ $$

Question Number 174376 Answers: 0 Comments: 6

if the mean of the data 1,2,3,4,..., 100 is 50.5 then what is the mean of the data 5,7,9,11,...,203??

$${if}\:{the}\:{mean}\:{of}\:{the}\:{data}\:\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},...,\:\mathrm{100} \\ $$$$\:{is}\:\mathrm{50}.\mathrm{5}\:{then}\:{what}\:{is}\:{the}\:{mean}\:{of}\:{the}\: \\ $$$${data}\:\mathrm{5},\mathrm{7},\mathrm{9},\mathrm{11},...,\mathrm{203}?? \\ $$$$ \\ $$

Question Number 174377 Answers: 1 Comments: 0

Question Number 174374 Answers: 2 Comments: 0

lim_(x→∞) (((x+3)/(x−2)))^x

$${li}\underset{{x}\rightarrow\infty} {{m}}\left(\frac{{x}+\mathrm{3}}{{x}−\mathrm{2}}\right)^{{x}} \\ $$

Question Number 174370 Answers: 0 Comments: 1

Question Number 174373 Answers: 0 Comments: 1

find ∫(√(x+(√(1−x))))dx

$${find}\:\int\sqrt{{x}+\sqrt{\mathrm{1}−{x}}}{dx} \\ $$

Question Number 174361 Answers: 0 Comments: 1

Question Number 175036 Answers: 1 Comments: 0

Solve the differential equation (xy^2 −1)dx−(x^2 y−1)dy=0

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation} \\ $$$$\left(\mathrm{xy}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{dx}−\left(\mathrm{x}^{\mathrm{2}} \mathrm{y}−\mathrm{1}\right)\mathrm{dy}=\mathrm{0} \\ $$

Question Number 174356 Answers: 2 Comments: 0

x^3 +4x^2 −9x−14=0 1. (1/x_1 ^2 )+(1/x_2 ^2 )+(1/x_3 ^2 )=? 2. Σ ((x_1 ^2 +x_2 ^2 )/x_3 )=?

$$\:\:\:\:\:\:\:\boldsymbol{{x}}^{\mathrm{3}} +\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{9}\boldsymbol{{x}}−\mathrm{14}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{1}.\:\frac{\mathrm{1}}{\boldsymbol{{x}}_{\mathrm{1}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{\boldsymbol{{x}}_{\mathrm{2}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{\boldsymbol{{x}}_{\mathrm{3}} ^{\mathrm{2}} }=? \\ $$$$\:\:\:\:\:\mathrm{2}.\:\Sigma\:\frac{\boldsymbol{{x}}_{\mathrm{1}} ^{\mathrm{2}} +\boldsymbol{{x}}_{\mathrm{2}} ^{\mathrm{2}} }{\boldsymbol{{x}}_{\mathrm{3}} }=? \\ $$

Question Number 174351 Answers: 1 Comments: 0

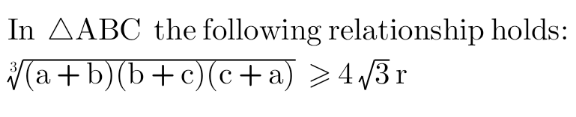
Question Number 174350 Answers: 0 Comments: 1

Question Number 174346 Answers: 1 Comments: 0

(1/(cos^2 10°)) +(1/(sin^2 20°)) +(1/(sin^2 40°)) −(1/(cos^2 45° ))=?

$$\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{10}°}\:+\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{20}°}\:+\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{40}°}\:−\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{45}°\:}=? \\ $$

Question Number 174341 Answers: 3 Comments: 1

1.∫_( 1) ^( 2) (√(x+(√(x−1)) )) dx=? 2. ∫_( 0) ^( (𝛑/2)) ((2sinx+4cosx)/(sinx+cosx)) dx=?

$$\:\:\:\:\mathrm{1}.\underset{\:\:\:\:\mathrm{1}} {\overset{\:\:\:\:\:\:\:\:\:\:\mathrm{2}} {\int}}\:\sqrt{\boldsymbol{{x}}+\sqrt{\boldsymbol{{x}}−\mathrm{1}}\:}\:\boldsymbol{{dx}}=? \\ $$$$\:\:\:\:\:\mathrm{2}.\:\:\:\underset{\:\:\:\:\:\mathrm{0}} {\overset{\:\:\:\:\:\:\:\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\int}}\:\:\frac{\mathrm{2}\boldsymbol{{sinx}}+\mathrm{4}\boldsymbol{{cosx}}}{\boldsymbol{{sinx}}+\boldsymbol{{cosx}}}\:\:\boldsymbol{{dx}}=? \\ $$

Question Number 174340 Answers: 0 Comments: 0

Question Number 174331 Answers: 0 Comments: 1

Question Number 174327 Answers: 1 Comments: 0

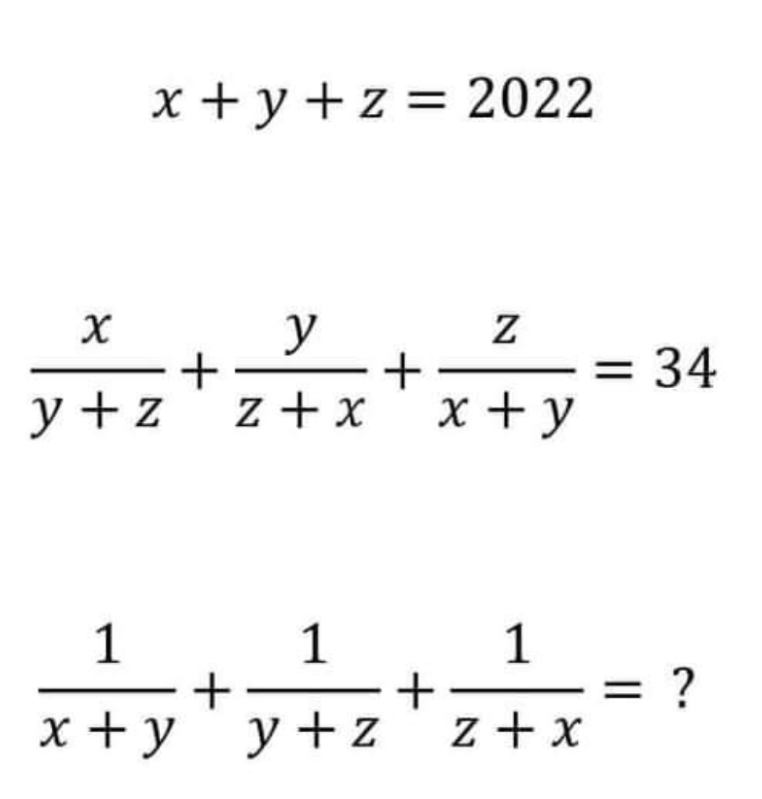
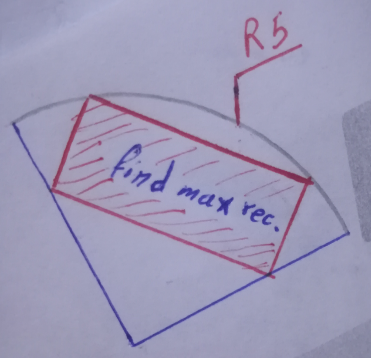
Question Number 174324 Answers: 2 Comments: 5

Factorize:− 2x^2 y^2 + 2y^2 z^2 + 2z^2 x^2 − x^4 − y^4 − z^4

$$\mathrm{F}{actorize}:− \\ $$$$\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \:+\:\mathrm{2}{y}^{\mathrm{2}} {z}^{\mathrm{2}} \:+\:\mathrm{2}{z}^{\mathrm{2}} {x}^{\mathrm{2}} \:−\:{x}^{\mathrm{4}} \:−\:{y}^{\mathrm{4}} \:−\:{z}^{\mathrm{4}} \\ $$

Question Number 176895 Answers: 2 Comments: 0

7C=log_2 (1/6)+log_3 27 Solve

$$\mathrm{7C}=\mathrm{log}_{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{6}}+\mathrm{log}_{\mathrm{3}} \mathrm{27} \\ $$$$ \\ $$$$\mathrm{Solve} \\ $$

Question Number 176894 Answers: 1 Comments: 0

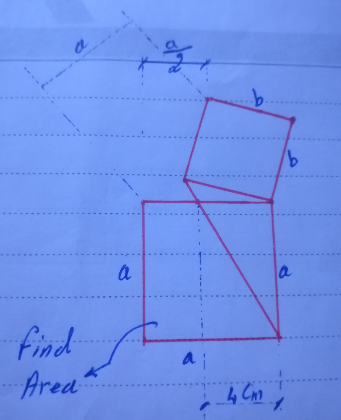
Question Number 176893 Answers: 1 Comments: 0

[4(x^2 +2) +(9/((x^2 +2)))]_(min)

$$\:\:\:\:\left[\mathrm{4}\left({x}^{\mathrm{2}} +\mathrm{2}\right)\:+\frac{\mathrm{9}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)}\right]_{\mathrm{min}} \\ $$

Question Number 176891 Answers: 1 Comments: 0

Question Number 174367 Answers: 0 Comments: 2

solve y^(10) ((dy/dx))+(y^(11) /((x−1)))=xy^(12)

$$\mathrm{solve} \\ $$$$\mathrm{y}^{\mathrm{10}} \left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)+\frac{\mathrm{y}^{\mathrm{11}} }{\left(\mathrm{x}−\mathrm{1}\right)}=\mathrm{xy}^{\mathrm{12}} \\ $$

Question Number 174315 Answers: 1 Comments: 0

Question Number 174304 Answers: 1 Comments: 0

Pg 440 Pg 441 Pg 442 Pg 443 Pg 444 Pg 445 Pg 446 Pg 447 Pg 448 Pg 449

Contact: info@tinkutara.com