Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 440

Question Number 175471 Answers: 1 Comments: 0

Question Number 175470 Answers: 1 Comments: 0

Question Number 175467 Answers: 0 Comments: 1

Question Number 175466 Answers: 0 Comments: 0

Question Number 175464 Answers: 2 Comments: 0

Find general solutions the following differential equations (a) (d^2 y/dx^2 ) + (dy/dx) = 6y (b) (3x^2 +y^2 )dx + (x^2 +y^2 )dy = 0

$$\:\mathrm{Find}\:\mathrm{general}\:\mathrm{solutions}\:\mathrm{the}\:\mathrm{following}\: \\ $$$$\mathrm{differential}\:\mathrm{equations} \\ $$$$\left({a}\right)\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\frac{{dy}}{{dx}}\:=\:\mathrm{6}{y} \\ $$$$\left(\mathrm{b}\right)\:\:\:\left(\mathrm{3}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){dx}\:+\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){dy}\:=\:\mathrm{0} \\ $$$$ \\ $$

Question Number 175462 Answers: 1 Comments: 3

p^3 +q^3 +p^2 +q^2 +c^2 =0 find p+q in terms of c. if c^2 <(4/9).

$${p}^{\mathrm{3}} +{q}^{\mathrm{3}} +{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${find}\:{p}+{q}\:{in}\:{terms}\:{of}\:{c}.\:\:{if}\:\:{c}^{\mathrm{2}} <\frac{\mathrm{4}}{\mathrm{9}}. \\ $$

Question Number 175525 Answers: 0 Comments: 0

Question Number 175521 Answers: 0 Comments: 0

Question Number 175454 Answers: 0 Comments: 0

Question Number 175452 Answers: 0 Comments: 0

Question Number 175449 Answers: 1 Comments: 1

Question Number 175450 Answers: 0 Comments: 0

Question Number 175443 Answers: 1 Comments: 0

solve for x 16^x +20^x = 25^x

$${solve}\:{for}\:{x} \\ $$$$\mathrm{16}^{{x}} +\mathrm{20}^{{x}} =\:\mathrm{25}^{{x}} \\ $$

Question Number 175436 Answers: 2 Comments: 2

∫((2x^2 +3)/( (√(3x+2))))=?

$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}}{\:\sqrt{\mathrm{3}{x}+\mathrm{2}}}=? \\ $$

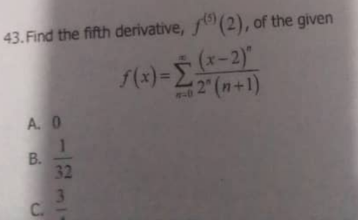
Question Number 175434 Answers: 1 Comments: 0

Question Number 175457 Answers: 3 Comments: 0

23+2323+232323+....(n terms)=?

$$ \\ $$$$\mathrm{23}+\mathrm{2323}+\mathrm{232323}+....\left({n}\:{terms}\right)=? \\ $$$$ \\ $$

Question Number 175430 Answers: 0 Comments: 2

Question Number 175426 Answers: 0 Comments: 0

Question Number 181496 Answers: 1 Comments: 0

Question Number 181494 Answers: 0 Comments: 0

Question Number 175458 Answers: 2 Comments: 0

2^m −2^n = 2016 find m and n

$$\mathrm{2}^{{m}} −\mathrm{2}^{{n}} =\:\mathrm{2016} \\ $$$${find}\:{m}\:{and}\:{n} \\ $$

Question Number 175420 Answers: 2 Comments: 0

solve for x 2^x .3^x^2 = 6

$${solve}\:{for}\:{x} \\ $$$$\mathrm{2}^{{x}} .\mathrm{3}^{{x}^{\mathrm{2}} } =\:\mathrm{6} \\ $$

Question Number 175411 Answers: 2 Comments: 3

7+67+667+6667+.....(n terms)=?

$$ \\ $$$$\mathrm{7}+\mathrm{67}+\mathrm{667}+\mathrm{6667}+.....\left({n}\:{terms}\right)=? \\ $$$$ \\ $$

Question Number 175410 Answers: 1 Comments: 0

A=∫9xcos 2x dx

$$\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{A}=\int\mathrm{9}{x}\mathrm{cos}\:\mathrm{2}{x}\:\:{dx} \\ $$$$ \\ $$

Question Number 175409 Answers: 1 Comments: 5

exercise Consider a polygon with an odd number 𝗻 of vertices. We connect any 3 vertices of this polygon to form a triangle. What is the probability that this triangle contains the center of the circle circumscribing the polygon?

$$\mathrm{exercise} \\ $$Consider a polygon with an odd number 𝗻 of vertices. We connect any 3 vertices of this polygon to form a triangle. What is the probability that this triangle contains the center of the circle circumscribing the polygon?

Question Number 175407 Answers: 2 Comments: 0

Trouver la somme de S_n Si S_n =1+11+111+...+1111...111

$$\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\underline{\mathrm{Trouver}\:\mathrm{la}\:\mathrm{somme}\:\mathrm{de}\:\mathrm{S}_{{n}} }\:\: \\ $$$$\:\:\:\mathrm{Si}\:\:\:\:\:\:{S}_{{n}} =\mathrm{1}+\mathrm{11}+\mathrm{111}+...+\mathrm{1111}...\mathrm{111}\:\:\:\:\:\:\:\: \\ $$$$ \\ $$

Pg 435 Pg 436 Pg 437 Pg 438 Pg 439 Pg 440 Pg 441 Pg 442 Pg 443 Pg 444

Contact: info@tinkutara.com