
AllQuestion and Answers: Page 436
Question Number 176486 Answers: 1 Comments: 0
Question Number 176485 Answers: 2 Comments: 1

Question Number 176482 Answers: 0 Comments: 0
Question Number 176472 Answers: 1 Comments: 0
Question Number 176468 Answers: 1 Comments: 1
Question Number 176462 Answers: 1 Comments: 1
Question Number 176458 Answers: 5 Comments: 0
Question Number 176453 Answers: 2 Comments: 0
Question Number 176449 Answers: 0 Comments: 0
Question Number 176448 Answers: 0 Comments: 3
Question Number 176768 Answers: 0 Comments: 0
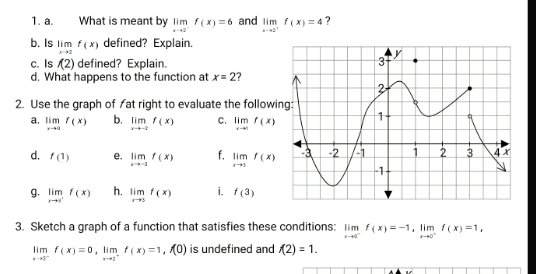
Question Number 176440 Answers: 0 Comments: 0

Question Number 176437 Answers: 1 Comments: 0
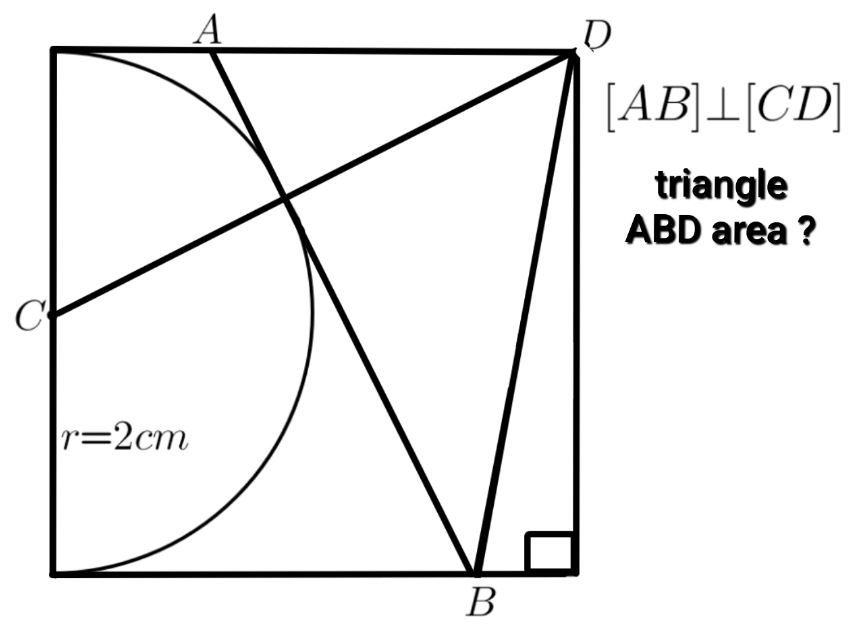
Question Number 176427 Answers: 0 Comments: 0
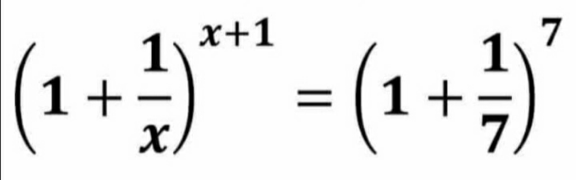
Question Number 176424 Answers: 0 Comments: 0
Question Number 176423 Answers: 1 Comments: 0

Question Number 176421 Answers: 2 Comments: 0

Question Number 176399 Answers: 2 Comments: 1
Question Number 176394 Answers: 0 Comments: 1
Question Number 176388 Answers: 1 Comments: 1
$$\:{find}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}+{sinx}}{{x}−{sinx}} \\ $$
Question Number 176387 Answers: 4 Comments: 5
Question Number 176384 Answers: 2 Comments: 0
Question Number 176393 Answers: 1 Comments: 0
Question Number 176391 Answers: 2 Comments: 1
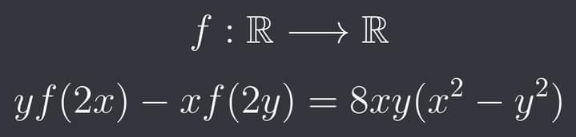
Question Number 176379 Answers: 1 Comments: 0
Question Number 176378 Answers: 0 Comments: 0

Pg 431 Pg 432 Pg 433 Pg 434 Pg 435 Pg 436 Pg 437 Pg 438 Pg 439 Pg 440
