
AllQuestion and Answers: Page 429
Question Number 177621 Answers: 1 Comments: 1
Question Number 177619 Answers: 0 Comments: 2
Question Number 177606 Answers: 2 Comments: 0
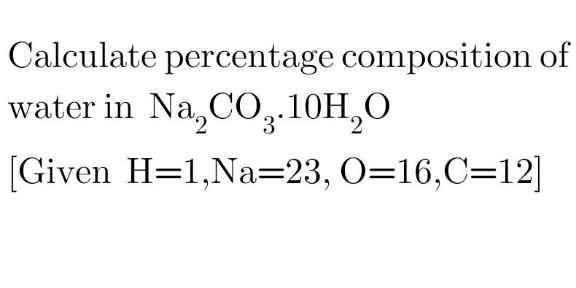
Question Number 177605 Answers: 2 Comments: 0

Question Number 177604 Answers: 0 Comments: 0
Question Number 177597 Answers: 2 Comments: 0
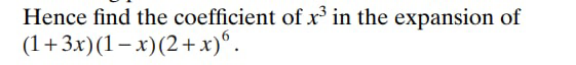
Question Number 177596 Answers: 1 Comments: 0

Question Number 177586 Answers: 1 Comments: 4

Question Number 177585 Answers: 0 Comments: 2
$${looks}\:{like}\:{my}\:{question}\:{was}\:{deleted}.\:{why}?\:{i}\:{cant}\:{find}\:{it} \\ $$
Question Number 177579 Answers: 2 Comments: 0
Question Number 177578 Answers: 1 Comments: 6
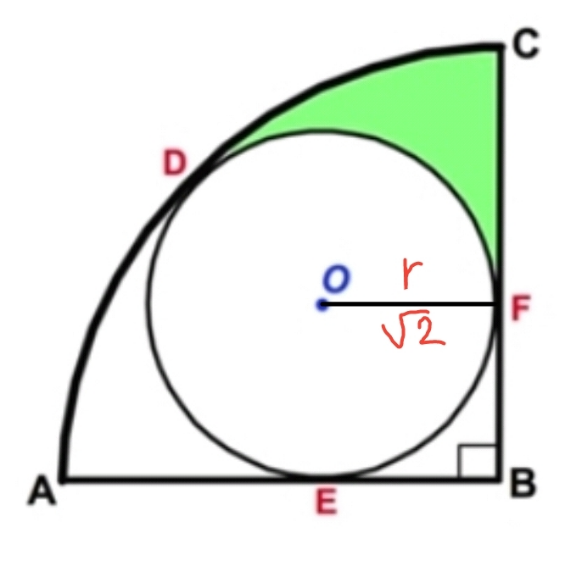
Question Number 177570 Answers: 1 Comments: 5
Question Number 177560 Answers: 2 Comments: 1

Question Number 177557 Answers: 0 Comments: 0

Question Number 177552 Answers: 0 Comments: 0

Question Number 177548 Answers: 2 Comments: 0
Question Number 177546 Answers: 0 Comments: 0
Question Number 177542 Answers: 3 Comments: 0
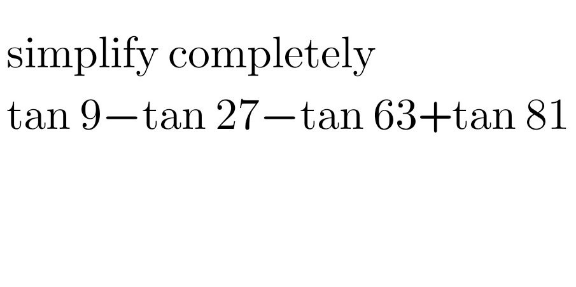
Question Number 177541 Answers: 0 Comments: 3

Question Number 177540 Answers: 2 Comments: 0

Question Number 177530 Answers: 3 Comments: 0
Question Number 177519 Answers: 2 Comments: 0

Question Number 177525 Answers: 1 Comments: 3

Question Number 177510 Answers: 1 Comments: 1

Question Number 177507 Answers: 1 Comments: 0
Question Number 177476 Answers: 1 Comments: 4

Pg 424 Pg 425 Pg 426 Pg 427 Pg 428 Pg 429 Pg 430 Pg 431 Pg 432 Pg 433
