
AllQuestion and Answers: Page 425
Question Number 178114 Answers: 1 Comments: 1
Question Number 178113 Answers: 1 Comments: 0
Question Number 178074 Answers: 0 Comments: 3
$${question}\:{posted}\:{by}\:{spillover}\:{in} \\ $$$$\mathrm{12}.\mathrm{10}.\mathrm{2022} \\ $$
Question Number 178073 Answers: 1 Comments: 4

Question Number 178067 Answers: 0 Comments: 0

Question Number 178064 Answers: 1 Comments: 0
Question Number 178058 Answers: 0 Comments: 0
Question Number 178059 Answers: 1 Comments: 1

Question Number 178054 Answers: 2 Comments: 3
Question Number 178052 Answers: 0 Comments: 0

Question Number 178051 Answers: 0 Comments: 0

Question Number 178037 Answers: 1 Comments: 1
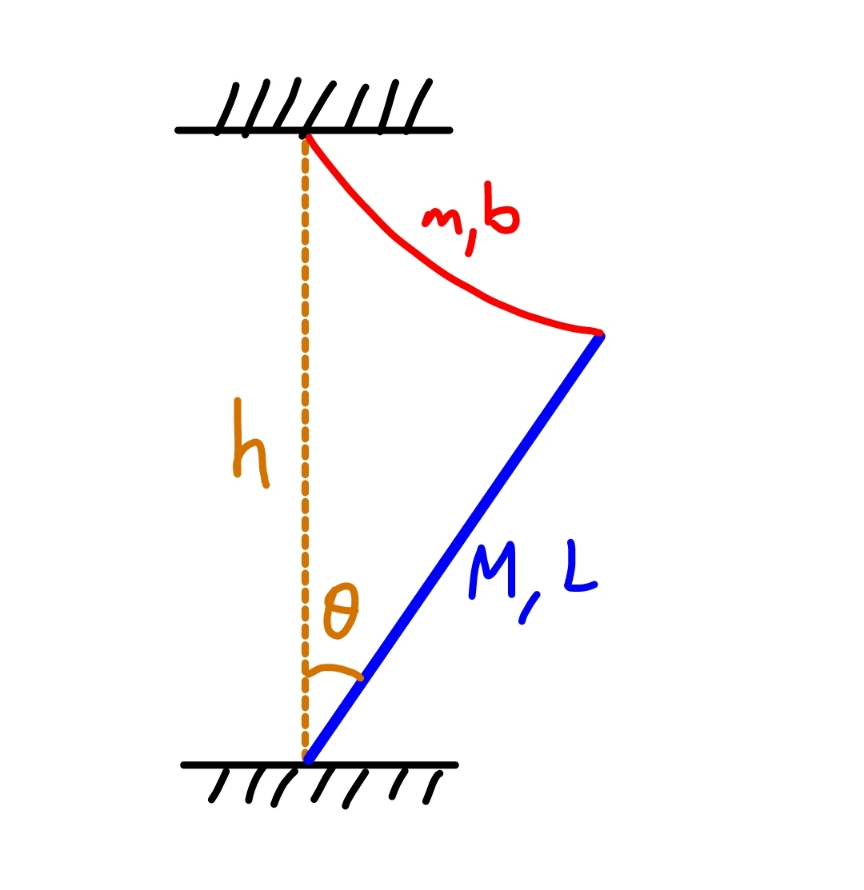
Question Number 178032 Answers: 0 Comments: 3
Question Number 178039 Answers: 0 Comments: 0
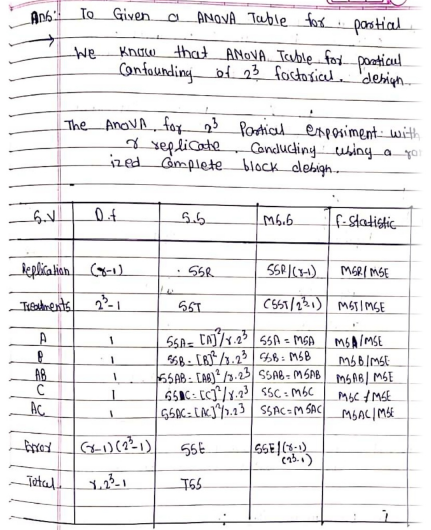
Question Number 178026 Answers: 1 Comments: 2

Question Number 178021 Answers: 1 Comments: 0
Question Number 178019 Answers: 0 Comments: 0
Question Number 178018 Answers: 2 Comments: 0
Question Number 178013 Answers: 4 Comments: 0
Question Number 178011 Answers: 3 Comments: 0
Question Number 178009 Answers: 3 Comments: 2

Question Number 178008 Answers: 1 Comments: 0

Question Number 178007 Answers: 1 Comments: 0

Question Number 178001 Answers: 1 Comments: 1
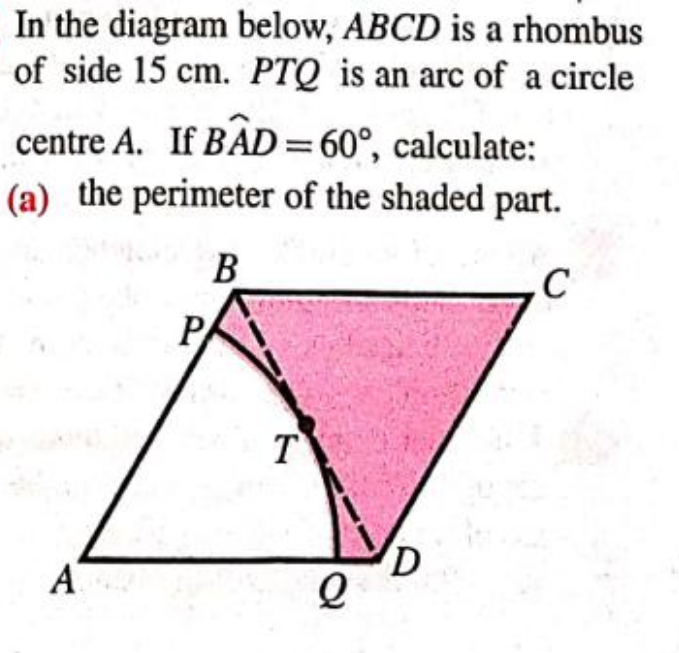
Question Number 177996 Answers: 0 Comments: 1

Question Number 177990 Answers: 0 Comments: 0

Pg 420 Pg 421 Pg 422 Pg 423 Pg 424 Pg 425 Pg 426 Pg 427 Pg 428 Pg 429
