
AllQuestion and Answers: Page 408
Question Number 180362 Answers: 0 Comments: 0
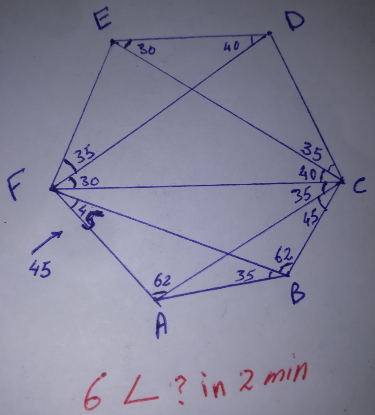
Question Number 180351 Answers: 0 Comments: 0
Question Number 180350 Answers: 1 Comments: 0

Question Number 180348 Answers: 0 Comments: 0

Question Number 180343 Answers: 1 Comments: 1
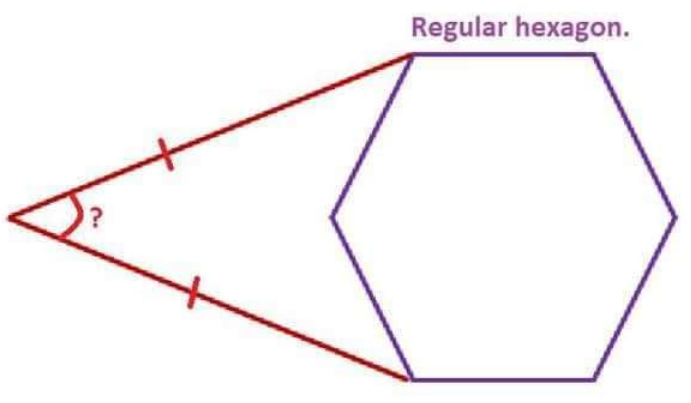
Question Number 180340 Answers: 1 Comments: 1
Question Number 180335 Answers: 2 Comments: 1
Question Number 180301 Answers: 3 Comments: 1

Question Number 180300 Answers: 3 Comments: 0

Question Number 180299 Answers: 1 Comments: 0

Question Number 180298 Answers: 1 Comments: 0
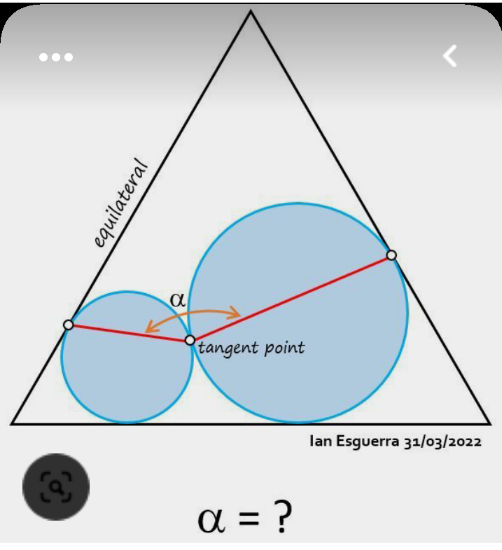
Question Number 180295 Answers: 0 Comments: 2
Question Number 180285 Answers: 0 Comments: 3
Question Number 180277 Answers: 0 Comments: 4
Question Number 180274 Answers: 1 Comments: 0
Question Number 180273 Answers: 0 Comments: 0
Question Number 180272 Answers: 0 Comments: 0
Question Number 180268 Answers: 2 Comments: 0
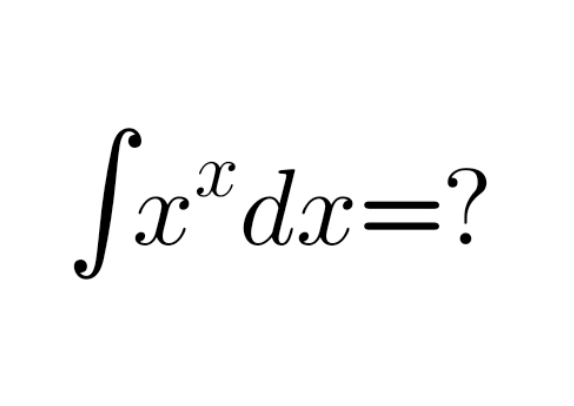
Question Number 180260 Answers: 1 Comments: 0
Question Number 180258 Answers: 2 Comments: 1

Question Number 180257 Answers: 2 Comments: 1

Question Number 180256 Answers: 3 Comments: 1

Question Number 180254 Answers: 1 Comments: 0

Question Number 180236 Answers: 0 Comments: 0
Question Number 180212 Answers: 1 Comments: 0
$${How}\:{many}\:{polygons}\:{can}\:{be}\:{formed} \\ $$$$\:{from}\:{a}\:{heptagon}?\: \\ $$
Question Number 180211 Answers: 1 Comments: 0
Pg 403 Pg 404 Pg 405 Pg 406 Pg 407 Pg 408 Pg 409 Pg 410 Pg 411 Pg 412
