Question and Answers Forum

AllQuestion and Answers: Page 401

Question Number 181593 Answers: 2 Comments: 0

I f , a^( 2) +5 b^( 2) + 4c^( 2) = 4b (a +c ) then , find the value of : E = (( ( b+ c −a )^( 3) )/( abc)) = ? ( abc ≠ 0 )

$$ \\ $$$$\:\:\:\:\:\:\:\mathrm{I}\:\mathrm{f}\:,\:\:\:\:{a}^{\:\mathrm{2}} \:+\mathrm{5}\:{b}^{\:\mathrm{2}} \:+\:\mathrm{4}{c}^{\:\mathrm{2}} =\:\mathrm{4}{b}\:\left({a}\:+{c}\:\right) \\ $$$$\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\mathrm{then}\:,\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:: \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{E}\:=\:\frac{\:\left(\:{b}+\:{c}\:−{a}\:\right)^{\:\mathrm{3}} }{\:{abc}}\:=\:?\:\:\:\:\left(\:{abc}\:\neq\:\mathrm{0}\:\right)\:\:\:\:\:\:\: \\ $$

Question Number 181592 Answers: 1 Comments: 0

prove that (1/(cos0 cos1 ))+(1/(cos1 cos2))+......+(1/(cos88 cos89))=((cos1)/(sin^2 1))

$${prove}\:{that} \\ $$$$\frac{\mathrm{1}}{{cos}\mathrm{0}\:{cos}\mathrm{1}\:}+\frac{\mathrm{1}}{{cos}\mathrm{1}\:{cos}\mathrm{2}}+......+\frac{\mathrm{1}}{{cos}\mathrm{88}\:{cos}\mathrm{89}}=\frac{{cos}\mathrm{1}}{{sin}^{\mathrm{2}} \mathrm{1}} \\ $$

Question Number 181590 Answers: 1 Comments: 0

Mr. Jibril is four times as old as his son. Four years ago, he was seven times as old as his son. In how many years will Mr Jibril′s age be twice his son′s age?

$$\mathrm{Mr}.\:\mathrm{Jibril}\:\mathrm{is}\:\mathrm{four}\:\mathrm{times}\:\mathrm{as}\:\mathrm{old}\:\mathrm{as}\:\mathrm{his}\:\mathrm{son}. \\ $$$$\mathrm{Four}\:\mathrm{years}\:\mathrm{ago},\:\mathrm{he}\:\mathrm{was}\:\mathrm{seven}\:\mathrm{times}\:\mathrm{as}\:\mathrm{old} \\ $$$$\mathrm{as}\:\mathrm{his}\:\mathrm{son}.\:\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{years}\:\mathrm{will}\:\mathrm{Mr} \\ $$$$\mathrm{Jibril}'\mathrm{s}\:\mathrm{age}\:\mathrm{be}\:\mathrm{twice}\:\mathrm{his}\:\mathrm{son}'\mathrm{s}\:\mathrm{age}? \\ $$

Question Number 181573 Answers: 0 Comments: 1

25^x − 4^x = 9^x fimd x

$$\mathrm{25}^{{x}} \:−\:\mathrm{4}^{{x}} \:=\:\mathrm{9}^{{x}} \\ $$$${fimd}\:{x} \\ $$

Question Number 181570 Answers: 1 Comments: 0

prove that:xε]−1,1[ Σ_(n=1) ^(+oo) (x^n /n)=−ln(1−x)

$$\left.{prove}\:{that}:{x}\epsilon\right]−\mathrm{1},\mathrm{1}\left[\right. \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+{oo}} {\sum}}\frac{{x}^{{n}} }{{n}}=−{ln}\left(\mathrm{1}−{x}\right) \\ $$

Question Number 181323 Answers: 2 Comments: 1

{ ((U_0 =1 et U_1 =2)),((U_(n+2) =(√(U_n U_(n+1) )))) :} determiner le terme generale et sa nature besoin d′aide avp

$$\begin{cases}{{U}_{\mathrm{0}} =\mathrm{1}\:{et}\:{U}_{\mathrm{1}} =\mathrm{2}}\\{{U}_{{n}+\mathrm{2}} =\sqrt{{U}_{{n}} {U}_{{n}+\mathrm{1}} }}\end{cases} \\ $$$${determiner}\:{le}\:{terme}\:{generale}\:{et}\:{sa}\:{nature} \\ $$$${besoin}\:{d}'{aide}\:{avp} \\ $$

Question Number 181319 Answers: 1 Comments: 0

Determiner 1. ∫(x/(x^4 +x^2 +1))dx 2. ∫((x^4 +1)/(x^4 +x^2 +1))dx

$${Determiner} \\ $$$$\mathrm{1}.\:\:\:\int\frac{{x}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\mathrm{2}.\:\:\:\int\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$

Question Number 181318 Answers: 2 Comments: 1

if x+y+z=0, find the maximum of ((∣x+2y+3z∣)/( (√(x^2 +y^2 +z^2 )))).

$${if}\:{x}+{y}+{z}=\mathrm{0},\:{find}\:{the}\:{maximum}\:{of} \\ $$$$\frac{\mid{x}+\mathrm{2}{y}+\mathrm{3}{z}\mid}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }}. \\ $$

Question Number 181313 Answers: 2 Comments: 0

Montrer que 3^(2n+1) +2^(n+2) est divisible par 7

$${Montrer}\:{que} \\ $$$$\mathrm{3}^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{2}^{{n}+\mathrm{2}} \:\:\:{est}\:{divisible}\:{par}\:\mathrm{7} \\ $$

Question Number 181296 Answers: 1 Comments: 0

Question Number 181312 Answers: 0 Comments: 0

Question Number 181280 Answers: 1 Comments: 0

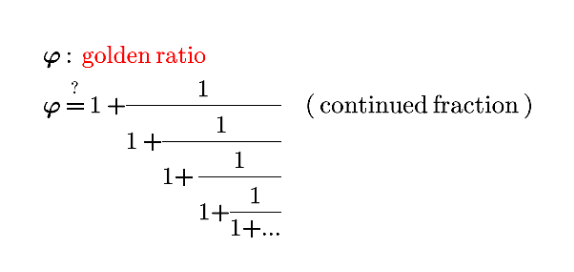
Question Number 181279 Answers: 3 Comments: 0

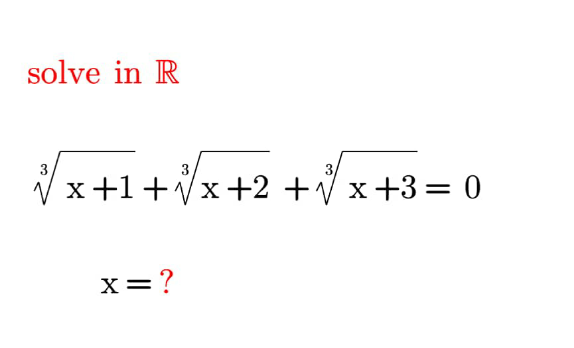
Question Number 181275 Answers: 1 Comments: 7

what is the sum of all even factors of 1000?

$${what}\:{is}\:{the}\:{sum}\:{of}\:{all} \\ $$$${even}\:{factors}\:{of}\:\mathrm{1000}? \\ $$

Question Number 181260 Answers: 2 Comments: 0

Calcul Σ_(n=3) ^(+∞) ((2n−1)/(n(n+2)(n−2)))=...??

$${Calcul}\: \\ $$$$\underset{{n}=\mathrm{3}} {\overset{+\infty} {\sum}}\:\frac{\mathrm{2}{n}−\mathrm{1}}{{n}\left({n}+\mathrm{2}\right)\left({n}−\mathrm{2}\right)}=...?? \\ $$

Question Number 181256 Answers: 0 Comments: 7

(1/f)=(n−1)((1/R_1 )−(1/R_2 )) lense′s maker equation. when is positive or negative R_1 and R_2 ?

$$\frac{\mathrm{1}}{{f}}=\left({n}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{{R}_{\mathrm{1}} }−\frac{\mathrm{1}}{{R}_{\mathrm{2}} }\right)\:\:{lense}'{s}\:{maker}\:{equation}. \\ $$$${when}\:{is}\:{positive}\:{or}\:{negative}\:{R}_{\mathrm{1}} \:{and}\:\:{R}_{\mathrm{2}} ? \\ $$

Question Number 181253 Answers: 0 Comments: 5

define microscopic and macroscopic with one one example.

$${define}\:{microscopic}\:{and}\:{macroscopic} \\ $$$${with}\:{one}\:{one}\:{example}. \\ $$

Question Number 181243 Answers: 1 Comments: 0

Solve for x : ((x − a^2 )/(b + c)) + ((x − b^2 )/(c + a)) + ((x − c^2 )/(a + b)) = 4(a + b + c)

$$\mathrm{Solve}\:\mathrm{for}\:{x}\:: \\ $$$$\frac{{x}\:−\:{a}^{\mathrm{2}} }{{b}\:+\:{c}}\:+\:\frac{{x}\:−\:{b}^{\mathrm{2}} }{{c}\:+\:{a}}\:+\:\frac{{x}\:−\:{c}^{\mathrm{2}} }{{a}\:+\:{b}}\:=\:\mathrm{4}\left({a}\:+\:{b}\:+\:{c}\right) \\ $$

Question Number 181238 Answers: 1 Comments: 0

calculer Σ_(n=1) ^(+oo) artan((2/n^2 ))

$${calculer} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+{oo}} {\sum}}{artan}\left(\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\right) \\ $$

Question Number 181232 Answers: 3 Comments: 1

Question Number 181221 Answers: 1 Comments: 0

Question Number 181219 Answers: 1 Comments: 0

Solve the D.E x(dy/dx)−y=(√(x^2 +y^2 )) .

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{D}.\mathrm{E} \\ $$$$\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{y}=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} } \\ $$$$ \\ $$$$. \\ $$

Question Number 181218 Answers: 1 Comments: 0

Solve the Differential equation: x(dy/dx)−y=2y(lnx−lny) .

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{Differential}\:\mathrm{equation}: \\ $$$$\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{y}=\mathrm{2y}\left(\mathrm{lnx}−\mathrm{lny}\right) \\ $$$$ \\ $$$$. \\ $$

Question Number 181217 Answers: 1 Comments: 0

Question Number 181207 Answers: 1 Comments: 0

cacul ∀x∈]0,1[ Σ_(n=0) ^(+∞) nx^n

$${cacul} \\ $$$$\left.\forall{x}\in\right]\mathrm{0},\mathrm{1}\left[\right. \\ $$$$\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}{nx}^{{n}} \\ $$

Question Number 181201 Answers: 3 Comments: 0

Pg 396 Pg 397 Pg 398 Pg 399 Pg 400 Pg 401 Pg 402 Pg 403 Pg 404 Pg 405

Contact: [email protected]