Question and Answers Forum

AllQuestion and Answers: Page 400

Question Number 181020 Answers: 1 Comments: 0

solve for x>0 ∫_0 ^x ⌊t⌋^2 dt=2(x−1) (Q180780 reposted)

$${solve}\:{for}\:{x}>\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{{x}} \lfloor{t}\rfloor^{\mathrm{2}} {dt}=\mathrm{2}\left({x}−\mathrm{1}\right) \\ $$$$ \\ $$$$\left({Q}\mathrm{180780}\:{reposted}\right) \\ $$

Question Number 181019 Answers: 1 Comments: 0

Question Number 181015 Answers: 1 Comments: 0

If z=xy−7x+4y, evaluate (∂z/(∂x )) and (∂z/∂y) .

$$\mathrm{If}\:\mathrm{z}=\mathrm{xy}−\mathrm{7x}+\mathrm{4y},\:\:\:\mathrm{evaluate}\:\frac{\partial\mathrm{z}}{\partial\mathrm{x}\:}\:\mathrm{and}\:\frac{\partial\mathrm{z}}{\partial\mathrm{y}} \\ $$$$ \\ $$$$. \\ $$$$ \\ $$

Question Number 181014 Answers: 0 Comments: 5

If f(x)=3−x^2 , find ((f(3+h)−f(3))/h) .

$$\mathrm{If}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{3}−\mathrm{x}^{\mathrm{2}} ,\:\:\:\:\mathrm{find}\:\frac{\mathrm{f}\left(\mathrm{3}+\mathrm{h}\right)−\mathrm{f}\left(\mathrm{3}\right)}{\mathrm{h}} \\ $$$$ \\ $$$$. \\ $$

Question Number 180998 Answers: 2 Comments: 0

Question Number 181007 Answers: 1 Comments: 0

[Question from Frix sir] ... I once played the game Tetris. You got points for each filled line, depending on how many lines you filled at once: 1 line = 1 point 2 lines = 3 points 3 lines = 6 points 4 lines = 10 points If you made 100 points, which possible combinations of lines did you fill when you filled 31 lines?

$$\left[{Question}\:{from}\:{Frix}\:{sir}\right] \\ $$$$...\:\mathrm{I}\:\mathrm{once}\:\mathrm{played}\:\mathrm{the}\:\mathrm{game}\:\mathrm{Tetris}.\: \\ $$$$\mathrm{You}\:\mathrm{got}\:\mathrm{points}\:\mathrm{for}\:\mathrm{each}\:\mathrm{filled}\:\mathrm{line},\: \\ $$$$\mathrm{depending}\:\mathrm{on}\:\mathrm{how}\:\mathrm{many}\:\mathrm{lines}\:\mathrm{you}\: \\ $$$$\mathrm{filled}\:\mathrm{at}\:\mathrm{once}: \\ $$$$\mathrm{1}\:\mathrm{line}\:=\:\mathrm{1}\:\mathrm{point} \\ $$$$\mathrm{2}\:\mathrm{lines}\:=\:\mathrm{3}\:\mathrm{points} \\ $$$$\mathrm{3}\:\mathrm{lines}\:=\:\mathrm{6}\:\mathrm{points} \\ $$$$\mathrm{4}\:\mathrm{lines}\:=\:\mathrm{10}\:\mathrm{points} \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{made}\:\mathrm{100}\:\mathrm{points},\:\mathrm{which}\:\mathrm{possible} \\ $$$$\mathrm{combinations}\:\mathrm{of}\:\mathrm{lines}\:\mathrm{did}\:\mathrm{you}\:\mathrm{fill}\:\mathrm{when} \\ $$$$\mathrm{you}\:\mathrm{filled}\:\mathrm{31}\:\mathrm{lines}? \\ $$

Question Number 180990 Answers: 1 Comments: 0

2 blondes hair of 6 girls will sit around a circular table, what′s the probability that those two girls sitting next to each other?

$$\mathrm{2}\:{blondes}\:{hair}\:{of}\:\mathrm{6}\:{girls}\:{will}\:{sit}\:{around}\:{a}\:{circular} \\ $$$$\:{table},\:{what}'{s}\:{the}\:{probability}\:{that}\:{those}\:{two}\:{girls} \\ $$$$\:{sitting}\:{next}\:{to}\:{each}\:{other}? \\ $$

Question Number 181572 Answers: 0 Comments: 0

2 𝚫 5=49 3 𝚫 4=36 4 𝚫 5=81 5 𝚫 5=?

$$ \\ $$$$\mathrm{2}\:\boldsymbol{\Delta}\:\mathrm{5}=\mathrm{49} \\ $$$$\mathrm{3}\:\boldsymbol{\Delta}\:\mathrm{4}=\mathrm{36} \\ $$$$\mathrm{4}\:\boldsymbol{\Delta}\:\mathrm{5}=\mathrm{81} \\ $$$$\mathrm{5}\:\boldsymbol{\Delta}\:\mathrm{5}=? \\ $$$$ \\ $$

Question Number 180977 Answers: 3 Comments: 0

what is larger, 3^(100) +4^(100) or 5^(100) ?

$${what}\:{is}\:{larger},\:\mathrm{3}^{\mathrm{100}} +\mathrm{4}^{\mathrm{100}} \:{or}\:\:\mathrm{5}^{\mathrm{100}} ? \\ $$

Question Number 180976 Answers: 2 Comments: 0

(dy/dx)=((x−y−2)/(x+y+6)) solve

$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{x}−\mathrm{y}−\mathrm{2}}{\mathrm{x}+\mathrm{y}+\mathrm{6}} \\ $$$$ \\ $$$$\mathrm{solve} \\ $$

Question Number 180974 Answers: 0 Comments: 1

Question Number 180954 Answers: 1 Comments: 0

A tugboat is travelling from Asaba to Onitsha across the River Niger with a resultant velocity of 20 knots. If the river flows at 12 knots, the direction of motion of the boat relative to the direction of water flow is?

Question Number 180953 Answers: 2 Comments: 0

What′s the smallest value of a^2 +b^2 +(1/(ab)) for a, b>0?

$${What}'{s}\:{the}\:{smallest}\:{value}\:{of} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\frac{\mathrm{1}}{{ab}}\:{for}\:{a},\:{b}>\mathrm{0}? \\ $$

Question Number 181066 Answers: 1 Comments: 1

Find the value of the expression: 2arcctg(tg3) − 3arctg(ctg2) a)2π−3 b)12 c)−6 d)π−4/2 e)3π/2

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{expression}: \\ $$$$\mathrm{2arcctg}\left(\mathrm{tg3}\right)\:−\:\mathrm{3arctg}\left(\mathrm{ctg2}\right) \\ $$$$\left.\mathrm{a}\left.\right)\left.\mathrm{2}\left.\pi\left.−\mathrm{3}\:\:\mathrm{b}\right)\mathrm{12}\:\:\mathrm{c}\right)−\mathrm{6}\:\:\mathrm{d}\right)\pi−\mathrm{4}/\mathrm{2}\:\:\mathrm{e}\right)\mathrm{3}\pi/\mathrm{2} \\ $$

Question Number 180943 Answers: 2 Comments: 0

if: a , bc^(−) = 1 + (1/2) + (3/(50)) find: a+b+c=?

$$\mathrm{if}:\:\:\:\overline {\mathrm{a}\:,\:\mathrm{bc}}\:=\:\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{3}}{\mathrm{50}} \\ $$$$\mathrm{find}:\:\:\:\mathrm{a}+\mathrm{b}+\mathrm{c}=? \\ $$

Question Number 180939 Answers: 0 Comments: 2

Question Number 180938 Answers: 2 Comments: 0

ab^(−) + ba^(−) = c3^(−) find: a+b+2c=?

$$\overline {\mathrm{ab}}\:+\:\overline {\mathrm{ba}}\:=\:\overline {\mathrm{c3}} \\ $$$$\mathrm{find}:\:\:\:\mathrm{a}+\mathrm{b}+\mathrm{2c}=? \\ $$

Question Number 180935 Answers: 2 Comments: 0

∫_ ((x+1)/(x^2 +1))dx

$$\int_{} \frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$

Question Number 180931 Answers: 0 Comments: 2

Question Number 180927 Answers: 2 Comments: 1

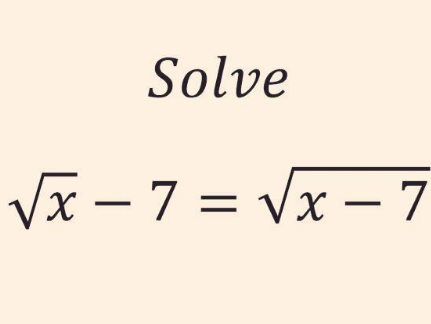
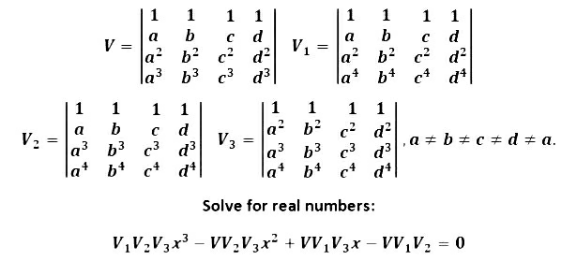
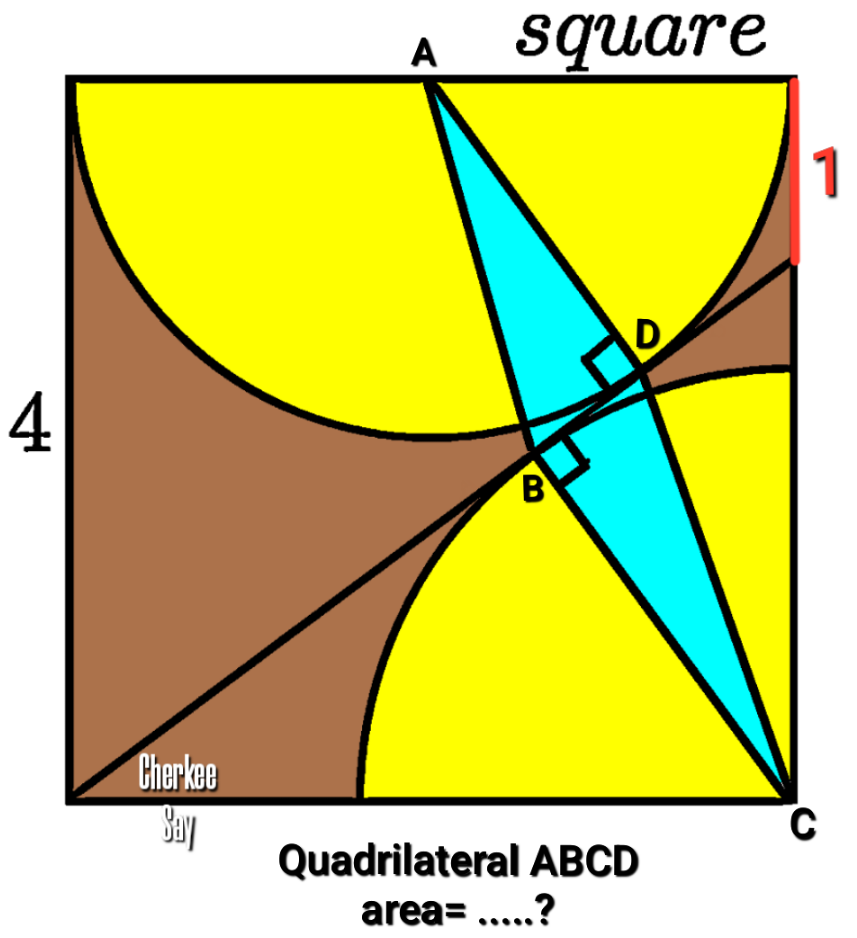
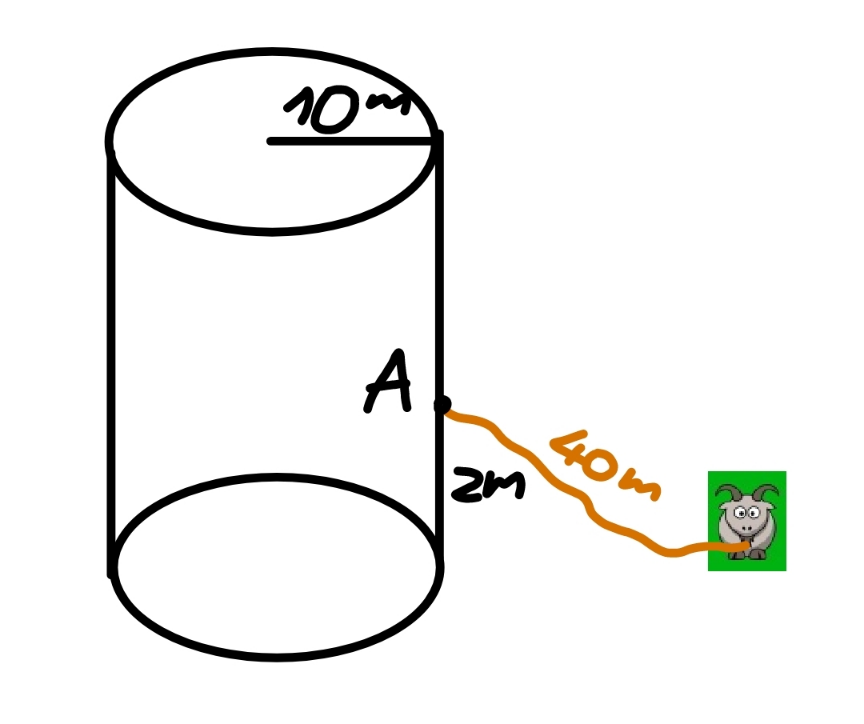
Question Number 180926 Answers: 0 Comments: 9

For this problem, we define the fractional part of x∈R_(≥0) as {x} = x − ⌊x⌋ where ⌊x⌋ is the integer part of x, i.e the greatest integer less than or equal to x. (a) Draw the function {x} in a cordinate system for 0≤x≤3 (b) Find the area A_n , under the graph of {x} between 0 and n∈N as given by A_n =∫_0 ^n {x}dx. M.m

$$\mathrm{For}\:\mathrm{this}\:\mathrm{problem},\:\mathrm{we}\:\mathrm{define}\:\mathrm{the}\: \\ $$$$\mathrm{fractional}\:\mathrm{part}\:\mathrm{of}\:\mathrm{x}\in\mathbb{R}_{\geqslant\mathrm{0}} \:\mathrm{as} \\ $$$$\left\{\mathrm{x}\right\}\:=\:\mathrm{x}\:−\:\lfloor\mathrm{x}\rfloor \\ $$$$\mathrm{where}\:\lfloor\mathrm{x}\rfloor\:\mathrm{is}\:\mathrm{the}\:\mathrm{integer}\:\mathrm{part}\:\mathrm{of}\:\mathrm{x},\:\mathrm{i}.\mathrm{e} \\ $$$$\mathrm{the}\:\mathrm{greatest}\:\mathrm{integer}\:\mathrm{less}\:\mathrm{than}\:\mathrm{or}\:\mathrm{equal} \\ $$$$\mathrm{to}\:\mathrm{x}. \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Draw}\:\mathrm{the}\:\mathrm{function}\:\left\{\mathrm{x}\right\}\:\mathrm{in}\:\mathrm{a}\:\mathrm{cordinate} \\ $$$$\mathrm{system}\:\mathrm{for}\:\mathrm{0}\leqslant\mathrm{x}\leqslant\mathrm{3} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{A}_{\mathrm{n}} \:,\:\mathrm{under}\:\mathrm{the}\:\mathrm{graph} \\ $$$$\mathrm{of}\:\left\{\mathrm{x}\right\}\:\mathrm{between}\:\mathrm{0}\:\mathrm{and}\:\mathrm{n}\in\mathbb{N}\:\mathrm{as}\:\mathrm{given}\:\mathrm{by} \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{n}} \left\{\mathrm{x}\right\}\mathrm{dx}. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 180923 Answers: 1 Comments: 0

Question Number 180919 Answers: 1 Comments: 0

Question Number 180917 Answers: 1 Comments: 0

Question Number 180890 Answers: 0 Comments: 2

We have 7 sets with 2 subsets each (yes and no are the 2 subsets of each of the 7 sets) how many possible combinations are there if one of the subset is picked for each of the 7 sets.

Question Number 180889 Answers: 0 Comments: 1

the average of 10 numbers is 5. the sum of their squares is 5000. how large can the largest number among them at most be and how small can the smallest number among them at most be?

$${the}\:{average}\:{of}\:\mathrm{10}\:{numbers}\:{is}\:\mathrm{5}.\:{the} \\ $$$${sum}\:{of}\:{their}\:{squares}\:{is}\:\mathrm{5000}.\:{how}\: \\ $$$${large}\:{can}\:{the}\:{largest}\:{number}\:{among} \\ $$$${them}\:{at}\:{most}\:{be}\:{and}\:{how}\:{small}\:{can}\: \\ $$$${the}\:{smallest}\:{number}\:{among}\:{them} \\ $$$${at}\:{most}\:{be}? \\ $$

Pg 395 Pg 396 Pg 397 Pg 398 Pg 399 Pg 400 Pg 401 Pg 402 Pg 403 Pg 404

Contact: info@tinkutara.com