Question and Answers Forum

AllQuestion and Answers: Page 389

Question Number 181138 Answers: 1 Comments: 0

If a + b + c = 0 then, (1/(2a^2 + bc)) + (1/(2b^2 + ca)) + (1/(2c^2 + ab)) = ?

$$\mathrm{If}\:{a}\:+\:{b}\:+\:{c}\:=\:\mathrm{0}\:\mathrm{then}, \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} \:+\:{bc}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{b}^{\mathrm{2}} \:+\:{ca}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{c}^{\mathrm{2}} \:+\:{ab}}\:=\:? \\ $$

Question Number 181153 Answers: 2 Comments: 0

Question Number 181130 Answers: 0 Comments: 0

Question Number 181128 Answers: 0 Comments: 2

Question Number 181154 Answers: 1 Comments: 0

(log_(15) 5)^2 +(log_(15) 3)(log_(15) 75)=?

$$\left({log}_{\mathrm{15}} \mathrm{5}\right)^{\mathrm{2}} +\left({log}_{\mathrm{15}} \mathrm{3}\right)\left({log}_{\mathrm{15}} \mathrm{75}\right)=? \\ $$$$ \\ $$

Question Number 181125 Answers: 1 Comments: 3

Let the acute triangle ΔABC have an outer circumscribed circle, whose tangents at the points B and C intersect at point P. Let D and E be the projections of perpendicular lines from point P on AC and AB. Prove that the interdection point of the heights of ΔADE is the midpoint of BC

$${Let}\:{the}\:{acute}\:{triangle}\:\Delta{ABC}\:\:{have} \\ $$$${an}\:{outer}\:{circumscribed}\:{circle}, \\ $$$${whose}\:{tangents}\:{at}\:{the}\:{points}\:{B}\:{and}\:{C} \\ $$$${intersect}\:{at}\:{point}\:{P}.\:{Let}\:{D}\:{and}\:{E}\:{be} \\ $$$${the}\:{projections}\:{of}\:{perpendicular} \\ $$$${lines}\:{from}\:{point}\:{P}\:{on}\:{AC}\:{and}\:{AB}. \\ $$$${Prove}\:{that}\:{the}\:{interdection}\:{point}\:{of} \\ $$$${the}\:{heights}\:{of}\:\Delta{ADE}\:{is}\:{the}\:{midpoint} \\ $$$${of}\:{BC} \\ $$

Question Number 181144 Answers: 3 Comments: 0

Solve for x : (((3x − 28)/(3x − 26)))^3 = ((x − 10)/(x − 8))

$$\mathrm{Solve}\:\mathrm{for}\:{x}\:: \\ $$$$\left(\frac{\mathrm{3}{x}\:−\:\mathrm{28}}{\mathrm{3}{x}\:−\:\mathrm{26}}\right)^{\mathrm{3}} \:=\:\frac{{x}\:−\:\mathrm{10}}{{x}\:−\:\mathrm{8}} \\ $$

Question Number 181104 Answers: 2 Comments: 1

lim_(x→∞) ((ln (1+(4/x)))/(π−arctan (2x))) =?

$$\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{x}}\right)}{\pi−\mathrm{arctan}\:\left(\mathrm{2x}\right)}\:=?\: \\ $$

Question Number 181099 Answers: 2 Comments: 0

prove that for every positivenumber p e q wee have: p+q≥(√(4pq))

$$ \\ $$$$\mathrm{prove}\:\mathrm{that}\:\mathrm{for}\:\mathrm{every}\: \\ $$$$\mathrm{positivenumber}\:\mathrm{p}\:\mathrm{e}\:\mathrm{q}\:\mathrm{wee} \\ $$$$\mathrm{hav}{e}: \\ $$$${p}+{q}\geqslant\sqrt{\mathrm{4}{pq}} \\ $$

Question Number 181089 Answers: 1 Comments: 0

Question Number 181085 Answers: 1 Comments: 3

Question Number 181084 Answers: 1 Comments: 0

Question Number 181079 Answers: 6 Comments: 2

Solve for x : (((x + a)/(x + b)))^3 = ((x + 2a − b)/(x − a + 2b))

$$\mathrm{Solve}\:\mathrm{for}\:{x}\:: \\ $$$$\left(\frac{{x}\:+\:{a}}{{x}\:+\:{b}}\right)^{\mathrm{3}} =\:\frac{{x}\:+\:\mathrm{2}{a}\:−\:{b}}{{x}\:−\:{a}\:+\:\mathrm{2}{b}} \\ $$

Question Number 181070 Answers: 2 Comments: 2

Question Number 181062 Answers: 0 Comments: 0

Q180886

$${Q}\mathrm{180886} \\ $$

Question Number 181055 Answers: 2 Comments: 14

Question Number 181052 Answers: 2 Comments: 3

Question Number 181051 Answers: 1 Comments: 0

Question Number 181041 Answers: 0 Comments: 0

If f(x)= x − ⌊ ((x−1)/3) ⌋ , g( x)= 2^( x) then , R_( gof) = ?

$$ \\ $$$$\:\:\:\mathrm{I}{f}\:\:\:\:{f}\left({x}\right)=\:{x}\:−\:\lfloor\:\frac{{x}−\mathrm{1}}{\mathrm{3}}\:\rfloor\:,\:\:{g}\left(\:{x}\right)=\:\mathrm{2}^{\:{x}} \\ $$$$\:\:\:\:\:\:\:{then}\:\:,\:\:\:\:\:\:{R}_{\:{gof}} \:=\:? \\ $$

Question Number 181039 Answers: 0 Comments: 3

Prove that for all a^2 divisible by b, a is also divisible by b for all a, b ∈ N

$${Prove}\:{that}\:{for}\:{all}\:{a}^{\mathrm{2}} \:{divisible}\:{by}\:{b}, \\ $$$${a}\:{is}\:{also}\:{divisible}\:{by}\:{b} \\ $$$${for}\:{all}\:{a},\:{b}\:\in\:\mathbb{N} \\ $$

Question Number 181053 Answers: 1 Comments: 0

An open pipe of r_o = 10 Cm, ℓ= 3m has an outer layer of ice that is melting at the rate of 2π Cm^3 per minute with thickness of 20 mm. How many days untill all the ice melts? and how fast is the thickness of the ice decreasing per hour?

$${An}\:{open}\:{pipe}\:{of}\:{r}_{{o}} =\:\mathrm{10}\:{Cm},\:\ell=\:\mathrm{3}{m}\:{has}\:{an}\:{outer} \\ $$$$\:{layer}\:{of}\:{ice}\:{that}\:{is}\:{melting}\:{at}\:{the}\:{rate}\:{of}\:\mathrm{2}\pi\:{Cm}^{\mathrm{3}} \\ $$$$\:{per}\:{minute}\:{with}\:{thickness}\:{of}\:\mathrm{20}\:{mm}.\:{How}\:{many} \\ $$$$\:{days}\:{untill}\:{all}\:{the}\:{ice}\:{melts}?\:{and}\:{how}\:{fast}\:{is}\:{the} \\ $$$$\:{thickness}\:{of}\:{the}\:{ice}\:{decreasing}\:{per}\:{hour}? \\ $$

Question Number 181025 Answers: 0 Comments: 1

Send you solutions to kinmatics@gmail.com

$$\mathrm{Send}\:\mathrm{you}\:\mathrm{solutions}\:\mathrm{to}\:\boldsymbol{\mathrm{kinmatics}}@\boldsymbol{\mathrm{gmail}}.\boldsymbol{\mathrm{com}} \\ $$

Question Number 181023 Answers: 1 Comments: 0

Question Number 181245 Answers: 1 Comments: 7

(x−(1/x))(x^(4/3) +x^(2/3) )=x^(1/3) (x^2 −(1/x^2 )) prove LHS=RHS

$$\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)\left(\mathrm{x}^{\frac{\mathrm{4}}{\mathrm{3}}} +\mathrm{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)=\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right) \\ $$$$ \\ $$$$\mathrm{prove}\:\mathrm{LHS}=\mathrm{RHS} \\ $$

Question Number 181251 Answers: 1 Comments: 1

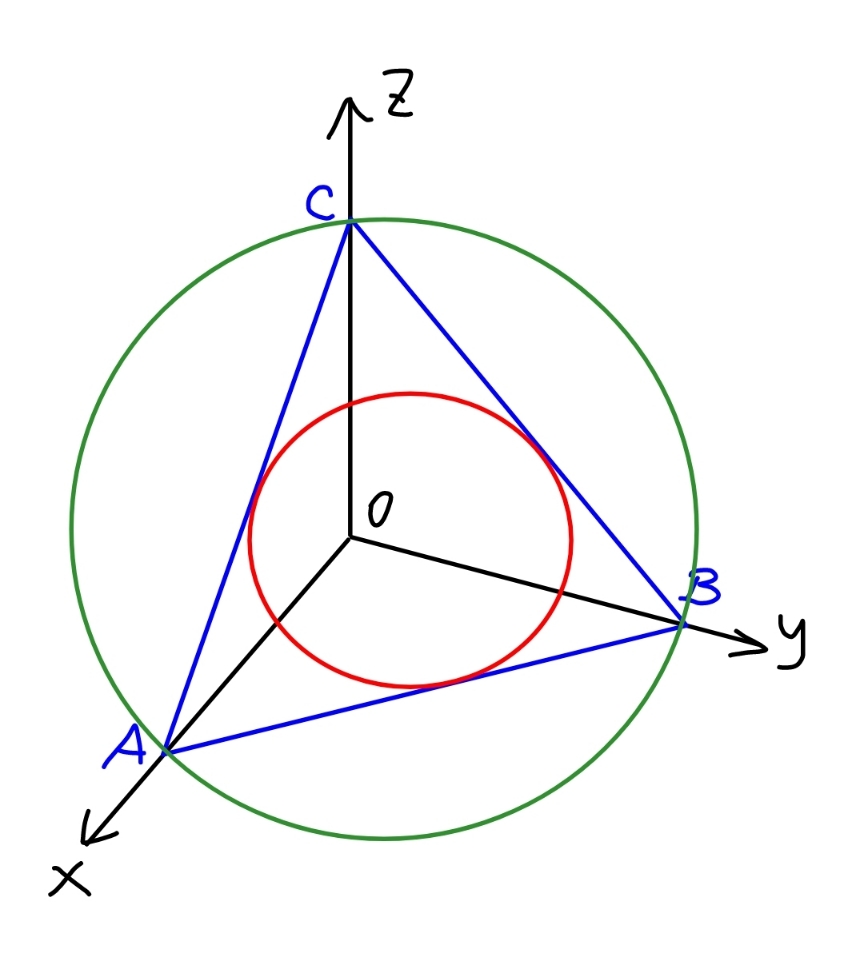
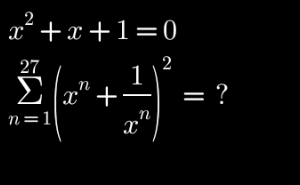
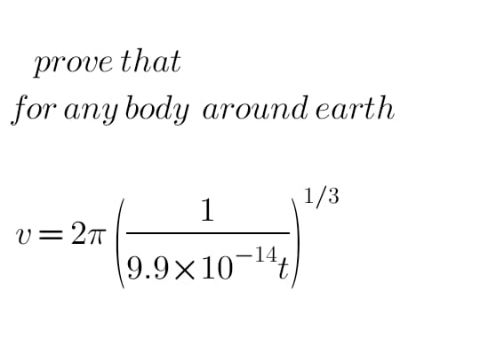
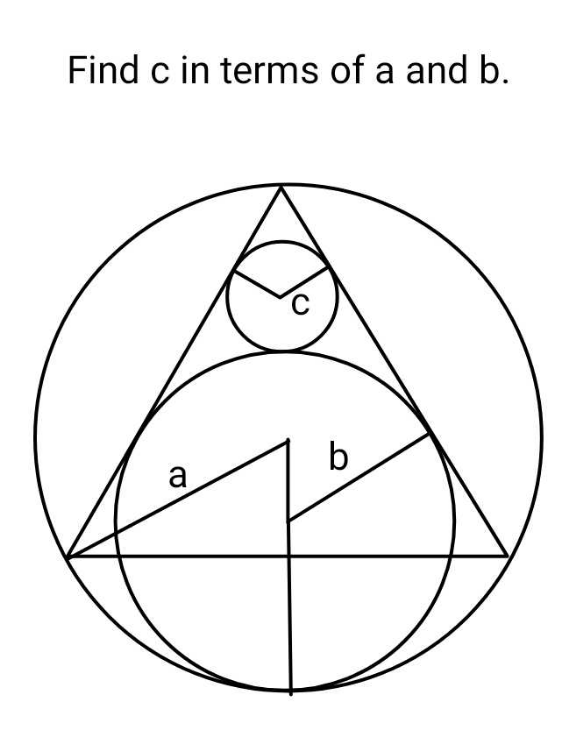
Question Number 181020 Answers: 1 Comments: 0

solve for x>0 ∫_0 ^x ⌊t⌋^2 dt=2(x−1) (Q180780 reposted)

$${solve}\:{for}\:{x}>\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{{x}} \lfloor{t}\rfloor^{\mathrm{2}} {dt}=\mathrm{2}\left({x}−\mathrm{1}\right) \\ $$$$ \\ $$$$\left({Q}\mathrm{180780}\:{reposted}\right) \\ $$

Pg 384 Pg 385 Pg 386 Pg 387 Pg 388 Pg 389 Pg 390 Pg 391 Pg 392 Pg 393

Contact: info@tinkutara.com