Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 380

Question Number 183845 Answers: 2 Comments: 0

Question Number 183844 Answers: 2 Comments: 0

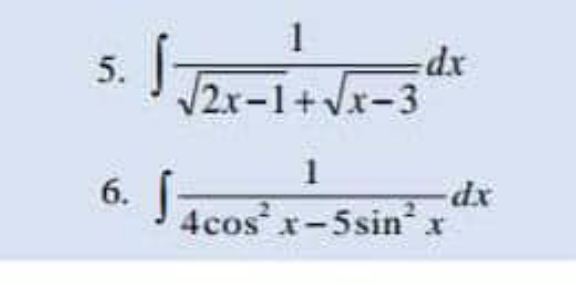
Question Number 183843 Answers: 1 Comments: 0

Question Number 183835 Answers: 2 Comments: 0

Resoudre le systeme abc =30 a+b+c =10 ab+bc+ac=31

$${Resoudre}\:{le}\:{systeme} \\ $$$$\:\:\mathrm{abc}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{30} \\ $$$$\:\:\:\mathrm{a}+\mathrm{b}+\mathrm{c}\:\:\:\:\:\:\:=\mathrm{10} \\ $$$$\:\:\:\mathrm{ab}+\mathrm{bc}+\mathrm{ac}=\mathrm{31} \\ $$$$ \\ $$

Question Number 183827 Answers: 1 Comments: 0

calcul: S=Σ_(n=2 ) ^(+oo) (n/((n^2 −1)^2 ))

$${calcul}:\:\:{S}=\underset{{n}=\mathrm{2}\:\:} {\overset{+{oo}} {\sum}}\frac{{n}}{\left({n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Question Number 183825 Answers: 1 Comments: 0

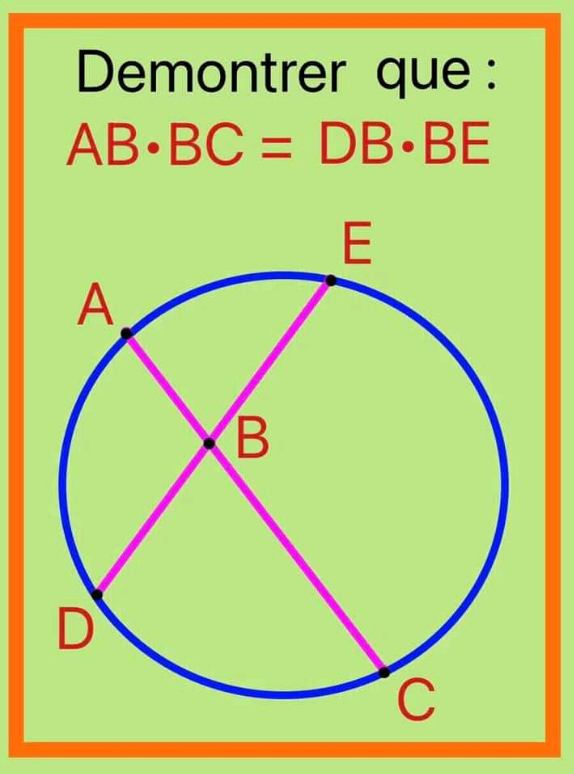
solve for x by using lambert function 2^x +3x=8

$${solve}\:{for}\:{x}\:{by}\:{using}\:{lambert}\:{function} \\ $$$$\mathrm{2}^{{x}} +\mathrm{3}{x}=\mathrm{8} \\ $$

Question Number 183815 Answers: 1 Comments: 0

Question Number 183814 Answers: 1 Comments: 0

determine eigen values and eigen vectors for each λ . and verify Ax=λx A= [(((√3)/2),(−(1/2))),((1/2),( ((√3)/2))) ]

$${determine}\:{eigen}\:{values}\:{and}\:{eigen}\:{vectors}\:{for} \\ $$$${each}\:\lambda\:.\:{and}\:{verify}\:{Ax}=\lambda{x} \\ $$$${A}=\begin{bmatrix}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}&{−\frac{\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{1}}{\mathrm{2}}}&{\:\:\:\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\end{bmatrix} \\ $$

Question Number 183806 Answers: 1 Comments: 0

∫ ((√(x+(√(x^2 +25))))/x) dx =?

$$\:\:\int\:\frac{\sqrt{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{25}}}}{{x}}\:{dx}\:=? \\ $$

Question Number 183803 Answers: 1 Comments: 0

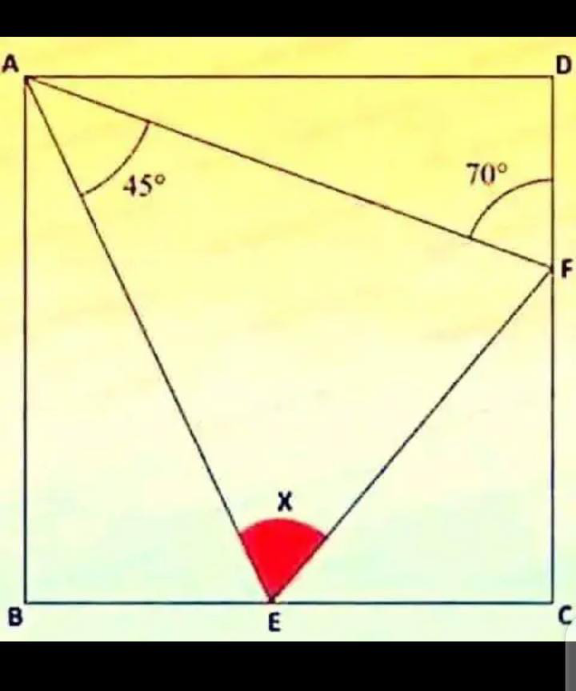
Question Number 183783 Answers: 0 Comments: 0

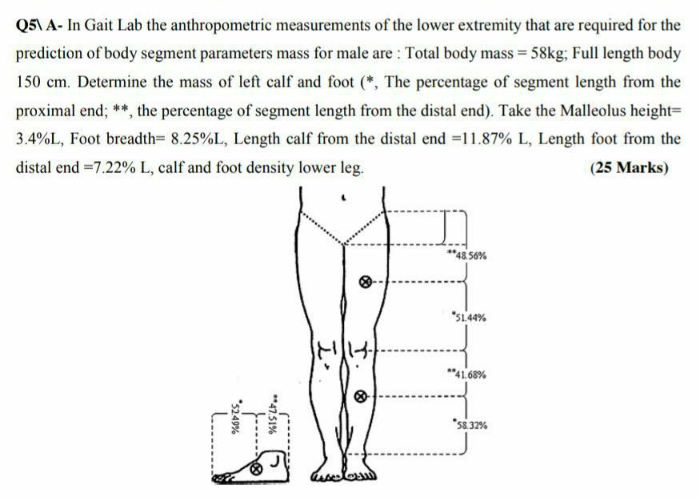
Question Number 183777 Answers: 2 Comments: 1

Question Number 183776 Answers: 0 Comments: 0

Question Number 183773 Answers: 2 Comments: 0

In a square (ABCD) there is a quarter of a circle ADC (AD = DC), put a point N in the arc AC such that AN = 1 and NC = 2(√2) find BN.

$$\:{In}\:{a}\:{square}\:\left({ABCD}\right)\:{there}\:{is}\:{a}\:{quarter}\:{of} \\ $$$$\:{a}\:{circle}\:{ADC}\:\left({AD}\:=\:{DC}\right),\:{put}\:{a}\:{point}\:{N} \\ $$$$\:{in}\:{the}\:{arc}\:{AC}\:{such}\:{that}\:{AN}\:=\:\mathrm{1}\:{and}\:{NC}\:=\:\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\:{find}\:{BN}.\: \\ $$$$\: \\ $$

Question Number 183767 Answers: 1 Comments: 0

Question Number 183766 Answers: 1 Comments: 0

Question Number 183769 Answers: 0 Comments: 4

solve for x: x^x^x =2^(2048) by using lambert function

$${solve}\:{for}\:{x}: \\ $$$${x}^{{x}^{{x}} } =\mathrm{2}^{\mathrm{2048}} \\ $$$${by}\:{using}\:{lambert}\:{function} \\ $$

Question Number 183761 Answers: 1 Comments: 0

Solve the differential equation for the function given by U(x,t). { (((∂U/∂t) = 2(∂^2 U/∂x^2 ) , 0 < x < π)),((U(0,t) = 0, U(π,t) = 0, t > 0)) :} U(x,0) = 25x

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation}\:\mathrm{for}\:\mathrm{the}\:\mathrm{function} \\ $$$$\mathrm{given}\:\mathrm{by}\:{U}\left({x},{t}\right). \\ $$$$\begin{cases}{\frac{\partial{U}}{\partial{t}}\:=\:\mathrm{2}\frac{\partial^{\mathrm{2}} {U}}{\partial{x}^{\mathrm{2}} }\:,\:\mathrm{0}\:<\:{x}\:<\:\pi}\\{{U}\left(\mathrm{0},{t}\right)\:=\:\mathrm{0},\:{U}\left(\pi,{t}\right)\:=\:\mathrm{0},\:{t}\:>\:\mathrm{0}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{U}\left({x},\mathrm{0}\right)\:=\:\mathrm{25}{x} \\ $$

Question Number 183795 Answers: 2 Comments: 0

Question Number 183794 Answers: 0 Comments: 1

If ∫_0 ^π ((cos x)/((x+2)^2 )) dx= T then ∫_0 ^π ((sin 2x)/(x+1)) dx = ?

$$\:{If}\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{cos}\:{x}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }\:{dx}=\:{T} \\ $$$$\:{then}\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{sin}\:\mathrm{2}{x}}{{x}+\mathrm{1}}\:{dx}\:=\:?\: \\ $$

Question Number 183756 Answers: 2 Comments: 0

solve for x by using lambert function x^2 =16^x

$${solve}\:{for}\:{x}\:{by}\:{using}\:{lambert}\:{function} \\ $$$${x}^{\mathrm{2}} =\mathrm{16}^{{x}} \\ $$

Question Number 183750 Answers: 1 Comments: 0

Question Number 183747 Answers: 1 Comments: 0

Find the perimeter of a regular heptagon ABCDEFG if (1/(AE)) + (1/(AC)) = (1/5)

$$\:{Find}\:{the}\:{perimeter}\:{of}\:{a}\:{regular}\:{heptagon}\: \\ $$$$\:{ABCDEFG}\:{if}\:\frac{\mathrm{1}}{{AE}}\:+\:\frac{\mathrm{1}}{{AC}}\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\: \\ $$

Question Number 183746 Answers: 1 Comments: 5

find x x^4 −x^3 −19x^2 +93x−128=0

$${find}\:{x} \\ $$$${x}^{\mathrm{4}} −{x}^{\mathrm{3}} −\mathrm{19}{x}^{\mathrm{2}} +\mathrm{93}{x}−\mathrm{128}=\mathrm{0} \\ $$

Question Number 183737 Answers: 2 Comments: 0

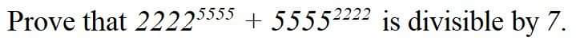
Question Number 183734 Answers: 1 Comments: 0

Pg 375 Pg 376 Pg 377 Pg 378 Pg 379 Pg 380 Pg 381 Pg 382 Pg 383 Pg 384

Contact: info@tinkutara.com