Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 369

Question Number 184828 Answers: 0 Comments: 1

Find x in terms of c ∀ 0<c<(2/(3(√3))) (3x^2 −1)(3x^2 +36x−1)^2 ={4(x^3 −x−c)+9(7x^2 +1)}^2

$${Find}\:{x}\:{in}\:{terms}\:{of}\:\:\:{c}\:\:\forall\:\mathrm{0}<{c}<\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{36}{x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=\left\{\mathrm{4}\left({x}^{\mathrm{3}} −{x}−{c}\right)+\mathrm{9}\left(\mathrm{7}{x}^{\mathrm{2}} +\mathrm{1}\right)\right\}^{\mathrm{2}} \\ $$

Question Number 184823 Answers: 1 Comments: 0

Lim_( x→ 0^( +) ) (( 1− cos ( 1− cos((√x) )))/x^( 4) )

$$ \\ $$$$\:\:\:\mathrm{Lim}_{\:{x}\rightarrow\:\mathrm{0}^{\:+} } \:\:\frac{\:\:\mathrm{1}−\:\:\mathrm{cos}\:\left(\:\mathrm{1}−\:\mathrm{cos}\left(\sqrt{{x}}\:\right)\right)}{{x}^{\:\mathrm{4}} } \\ $$

Question Number 184822 Answers: 1 Comments: 0

Question Number 184819 Answers: 2 Comments: 0

For 0≤x≤1 , maximum value of f(x)=x(√(1−x+(√(1−x)))) is __

$$\:\:{For}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:,\:{maximum}\:{value} \\ $$$$\:\:{of}\:{f}\left({x}\right)={x}\sqrt{\mathrm{1}−{x}+\sqrt{\mathrm{1}−{x}}}\:{is}\:\_\_ \\ $$

Question Number 184798 Answers: 0 Comments: 1

Show that lim_(x→0) (x/(∣x∣)) does not exist

$${Show}\:{that}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{\mid{x}\mid}\:\:{does}\:{not}\:{exist} \\ $$

Question Number 184797 Answers: 0 Comments: 1

Show that lim_(x→0) ((e^(1/x) −1)/(e^(1/x) +1)) does not exist

$${Show}\:{that}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\frac{\mathrm{1}}{{x}}} −\mathrm{1}}{{e}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}}\:\:\:{does}\:{not}\:{exist} \\ $$

Question Number 184796 Answers: 1 Comments: 2

Evaluate lim_(x→(π/6)) (((√3)sin x−cos x)/(x−(π/6)))

$${Evaluate}\: \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{6}}} {\mathrm{lim}}\frac{\sqrt{\mathrm{3}}\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{{x}−\frac{\pi}{\mathrm{6}}} \\ $$

Question Number 184795 Answers: 1 Comments: 1

Evaluate lim_(x→0) ((1−cos x(√(cos 2x)) )/x^2 )

$${Evaluate}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{x}\sqrt{\mathrm{cos}\:\mathrm{2}{x}}\:}{{x}^{\mathrm{2}} } \\ $$

Question Number 184794 Answers: 4 Comments: 2

Evaluate lim_(x→2) ((x^5 −32)/(x^3 −8))

$${Evaluate}\: \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{5}} −\mathrm{32}}{{x}^{\mathrm{3}} −\mathrm{8}} \\ $$

Question Number 184793 Answers: 1 Comments: 0

Evaluate lim_(x→2) ((x^2 −4)/( (√(3x−2))−(√(x+2))))

$${Evaluate}\: \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\:\frac{{x}^{\mathrm{2}} −\mathrm{4}}{\:\sqrt{\mathrm{3}{x}−\mathrm{2}}−\sqrt{{x}+\mathrm{2}}} \\ $$$$ \\ $$

Question Number 184792 Answers: 1 Comments: 2

Evaluate lim_(x→0) ((tan x−sin x)/(sin^3 x))

$${Evaluate}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:{x}−\mathrm{sin}\:{x}}{\mathrm{sin}\:^{\mathrm{3}} {x}} \\ $$$$ \\ $$

Question Number 184791 Answers: 0 Comments: 2

Evaluate lim_(x→0) ((e^x +e^(−x) −2)/x^2 )

$${Evaluate}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{{e}^{{x}} +{e}^{−{x}} −\mathrm{2}}{{x}^{\mathrm{2}} } \\ $$

Question Number 184790 Answers: 2 Comments: 2

Evaluate lim_(x→0) (((1+x)^6 −1)/((1+x)^5 −1))

$${Evaluate} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{6}} −\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{5}} −\mathrm{1}} \\ $$

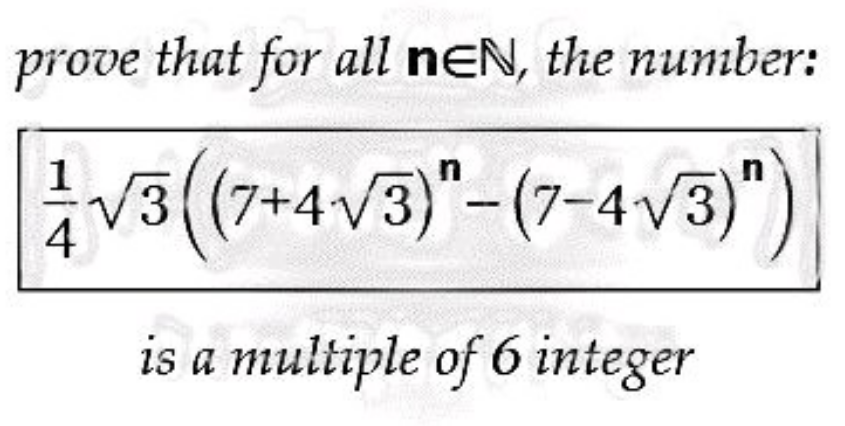
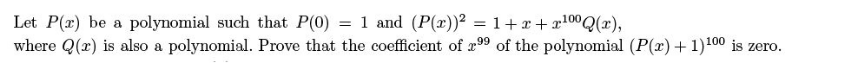
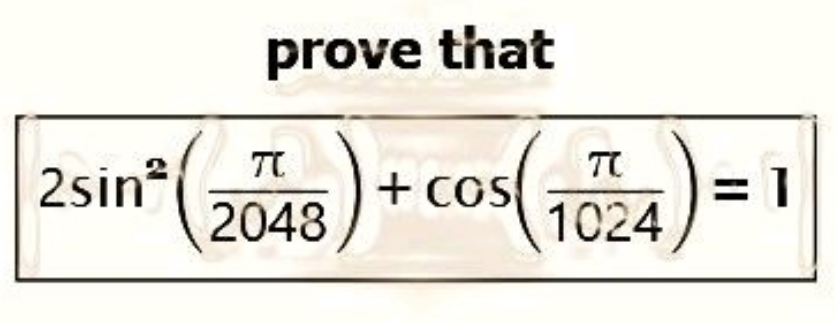
Question Number 184787 Answers: 0 Comments: 2

x^4 +16x^3 +9x^2 +256x+256=0 Find the values of x?

$$\mathrm{x}^{\mathrm{4}} +\mathrm{16x}^{\mathrm{3}} +\mathrm{9x}^{\mathrm{2}} +\mathrm{256x}+\mathrm{256}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{x}? \\ $$

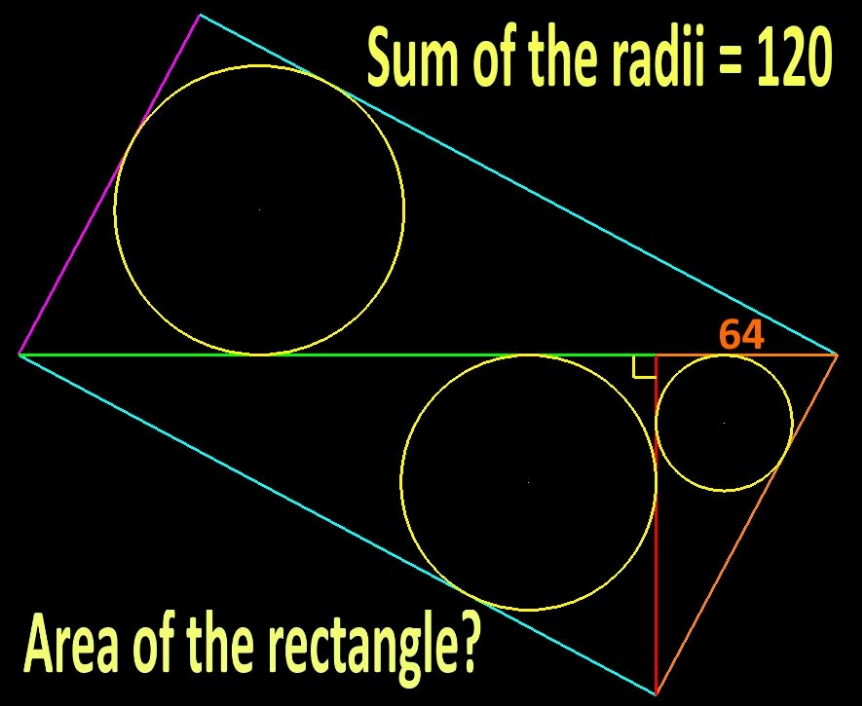
Question Number 184775 Answers: 1 Comments: 2

(1/(6 + (9/(6 + ((25)/(6 + ((49)/(6 + ((81)/(6+ ......)) )) )) )) )) =?

$$\:\:\:\: \\ $$$$\:\:\:\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{6}\:+\:\frac{\mathrm{9}}{\mathrm{6}\:+\:\:\frac{\mathrm{25}}{\mathrm{6}\:\:+\:\:\frac{\mathrm{49}}{\mathrm{6}\:+\:\frac{\mathrm{81}}{\mathrm{6}+\:......}\:\:\:\:\:}\:\:\:\:\:}\:\:}\:\:\:\:\:\:\:\:}\:\:=? \\ $$$$ \\ $$$$ \\ $$

Question Number 184774 Answers: 1 Comments: 2

Calcul the sum 1.Σx(1+x^2 )^(1/2) 2.Σxarctan(x) 3.Σe^x sinx 4.Σ(2x+1)^(20) 5.Σ(√(a^2 −x^2 )) a>0 6.Σxsinx

$${Calcul}\:{the}\:{sum} \\ $$$$\mathrm{1}.\Sigma{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{2}.\Sigma{xarctan}\left({x}\right) \\ $$$$\mathrm{3}.\Sigma{e}^{{x}} {sinx} \\ $$$$\mathrm{4}.\Sigma\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{20}} \\ $$$$\mathrm{5}.\Sigma\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} \:}\:{a}>\mathrm{0} \\ $$$$\mathrm{6}.\Sigma{xsinx} \\ $$

Question Number 184773 Answers: 2 Comments: 1

lim_(x→1) ((ax+b)/( (√(1+3x))−2))=c 2a−2b+3c=? (a,b,c)≠0 pease solution????

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{ax}+\mathrm{b}}{\:\sqrt{\mathrm{1}+\mathrm{3x}}−\mathrm{2}}=\mathrm{c} \\ $$$$\mathrm{2a}−\mathrm{2b}+\mathrm{3c}=? \\ $$$$\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)\neq\mathrm{0} \\ $$$$\mathrm{pease}\:\mathrm{solution}???? \\ $$

Question Number 184769 Answers: 0 Comments: 2

Question Number 184768 Answers: 1 Comments: 1

Σ_(n=o) ^(+oo) (x^n /(4n^2 −1))

$$\underset{{n}={o}} {\overset{+{oo}} {\sum}}\:\frac{{x}^{{n}} }{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}} \\ $$

Question Number 184757 Answers: 2 Comments: 2

Which function has a crisis point? a)y=x^3 +2x+6 b)y=(x)^(1/4) c)y=((15)/x) d)y=e^x e)y=(x)^(1/3)

$$\mathrm{Which}\:\mathrm{function}\:\mathrm{has}\:\mathrm{a}\:\mathrm{crisis}\:\mathrm{point}? \\ $$$$\left.\mathrm{a}\right)\mathrm{y}=\mathrm{x}^{\mathrm{3}} +\mathrm{2x}+\mathrm{6} \\ $$$$\left.\mathrm{b}\right)\mathrm{y}=\sqrt[{\mathrm{4}}]{\mathrm{x}} \\ $$$$\left.\mathrm{c}\right)\mathrm{y}=\frac{\mathrm{15}}{\mathrm{x}} \\ $$$$\left.\mathrm{d}\right)\mathrm{y}=\mathrm{e}^{\boldsymbol{\mathrm{x}}} \\ $$$$\left.\mathrm{e}\right)\mathrm{y}=\sqrt[{\mathrm{3}}]{\mathrm{x}} \\ $$

Question Number 184753 Answers: 1 Comments: 0

Question Number 184744 Answers: 1 Comments: 1

given that the 5th term of an AP is more than its firs term by 12. and the 6th term is more than the first term by 10. find the fist term? common difference and 100th term

$${given}\:{that}\:{the}\:\mathrm{5}{th}\:{term}\:{of}\:{an}\:{AP}\:{is}\:{more}\:{than}\:{its}\:{firs}\:{term}\:{by}\:\mathrm{12}.\:{and}\:{the}\:\mathrm{6}{th}\:{term}\:{is}\:{more}\:{than}\:{the}\:{first}\:{term}\:{by}\:\mathrm{10}.\:{find}\:{the}\:{fist}\:{term}?\:{common}\:{difference}\:{and}\:\mathrm{100}{th}\:{term} \\ $$$$ \\ $$

Question Number 184739 Answers: 1 Comments: 1

Number of linear functions be defined f:[−1, 1]→[0,2] is a)1 b)2 c)3 d)4

$${Number}\:{of}\:{linear}\:{functions}\: \\ $$$${be}\:{defined}\:{f}:\left[−\mathrm{1},\:\mathrm{1}\right]\rightarrow\left[\mathrm{0},\mathrm{2}\right]\:{is} \\ $$$$\left.{a}\left.\right)\left.\mathrm{1}\left.\:\:\:\:{b}\right)\mathrm{2}\:\:\:\:{c}\right)\mathrm{3}\:\:\:{d}\right)\mathrm{4} \\ $$

Question Number 184738 Answers: 1 Comments: 0

α , β are roots of , x^( 2) −x−1=0 ( α > β ) and , t_( n) = ((α^( n) − β^( n) )/(α−β)) ( n ∈ N ), if , b_1 =1 , b_( n) = t_( n−1) +t_( n−2) ( n ≥2 ) find the value of S = Σ_(n=1) ^∞ (( b_( n) )/(10^( n) )) =?

$$ \\ $$$$\alpha\:\:,\:\beta\:\:{are}\:{roots}\:{of}\:\:,\:{x}^{\:\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\:\:\alpha\:>\:\beta\:\right)\:{and}\:,\:\:{t}_{\:{n}} =\:\frac{\alpha^{\:{n}} −\:\beta^{\:{n}} }{\alpha−\beta} \\ $$$$\:\left(\:{n}\:\in\:\mathbb{N}\:\right),\:{if}\:,\:{b}_{\mathrm{1}} =\mathrm{1}\:,\:{b}_{\:{n}} =\:{t}_{\:{n}−\mathrm{1}} +{t}_{\:{n}−\mathrm{2}} \\ $$$$\:\:\:\left(\:{n}\:\geqslant\mathrm{2}\:\right)\:{find}\:{the}\:{value}\:{of} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:{b}_{\:{n}} }{\mathrm{10}^{\:{n}} }\:=? \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Question Number 184735 Answers: 0 Comments: 3

f(x,y)=((√(3xy^2 )))(((x^5 y^2 ))^(1/5) ) f^′ (x,y)=? f′′(x,y)=?

$$ \\ $$$${f}\left({x},{y}\right)=\left(\sqrt{\mathrm{3}{xy}^{\mathrm{2}} }\right)\left(\sqrt[{\mathrm{5}}]{{x}^{\mathrm{5}} {y}^{\mathrm{2}} }\right) \\ $$$${f}^{'} \left({x},{y}\right)=?\:\:\:\:\:{f}''\left({x},{y}\right)=? \\ $$$$ \\ $$

Question Number 184731 Answers: 1 Comments: 0

Express this function in both its Cartesian and polar form f(z) = ze^(iz) . Help!

$$\mathrm{Express}\:\mathrm{this}\:\mathrm{function}\:\mathrm{in}\:\mathrm{both}\:\mathrm{its} \\ $$$$\mathrm{Cartesian}\:\mathrm{and}\:\mathrm{polar}\:\mathrm{form} \\ $$$$\mathrm{f}\left(\mathrm{z}\right)\:=\:\mathrm{ze}^{\mathrm{iz}} . \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Pg 364 Pg 365 Pg 366 Pg 367 Pg 368 Pg 369 Pg 370 Pg 371 Pg 372 Pg 373

Terms of Service

Contact: info@tinkutara.com