Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 366

Question Number 185405 Answers: 1 Comments: 0

lim_(x→∞) (((x+2)^(1/x) −x^(1/x) )/((x+3)^(1/x) −x^(1/x) )) =?

$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left({x}+\mathrm{2}\right)^{\mathrm{1}/{x}} −{x}^{\mathrm{1}/{x}} }{\left({x}+\mathrm{3}\right)^{\mathrm{1}/{x}} −{x}^{\mathrm{1}/{x}} }\:=? \\ $$

Question Number 185403 Answers: 2 Comments: 0

Σ_(k=1) ^(16) ((√k)−(√(k−1)))=?

$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{16}} {\sum}}\left(\sqrt{{k}}−\sqrt{{k}−\mathrm{1}}\right)=? \\ $$

Question Number 185402 Answers: 0 Comments: 0

Question Number 185401 Answers: 0 Comments: 1

Show that ((1+z)/(1−z)) + ((1+z^ )/(1−z^ )) = ((2(1−∣z∣^2 ))/(∣1−z∣^2 )) Where z is a complex number Help!

$$\mathrm{Show}\:\mathrm{that}\:\frac{\mathrm{1}+\mathrm{z}}{\mathrm{1}−\mathrm{z}}\:+\:\frac{\mathrm{1}+\bar {\mathrm{z}}}{\mathrm{1}−\bar {\mathrm{z}}}\:=\:\frac{\mathrm{2}\left(\mathrm{1}−\mid\mathrm{z}\mid^{\mathrm{2}} \right)}{\mid\mathrm{1}−\mathrm{z}\mid^{\mathrm{2}} } \\ $$$$\mathrm{Where}\:\mathrm{z}\:\mathrm{is}\:\mathrm{a}\:\mathrm{complex}\:\mathrm{number} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Question Number 185395 Answers: 1 Comments: 0

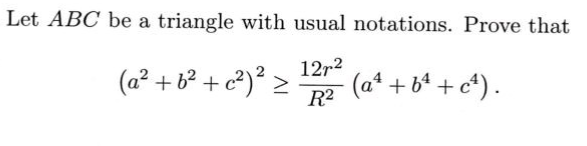
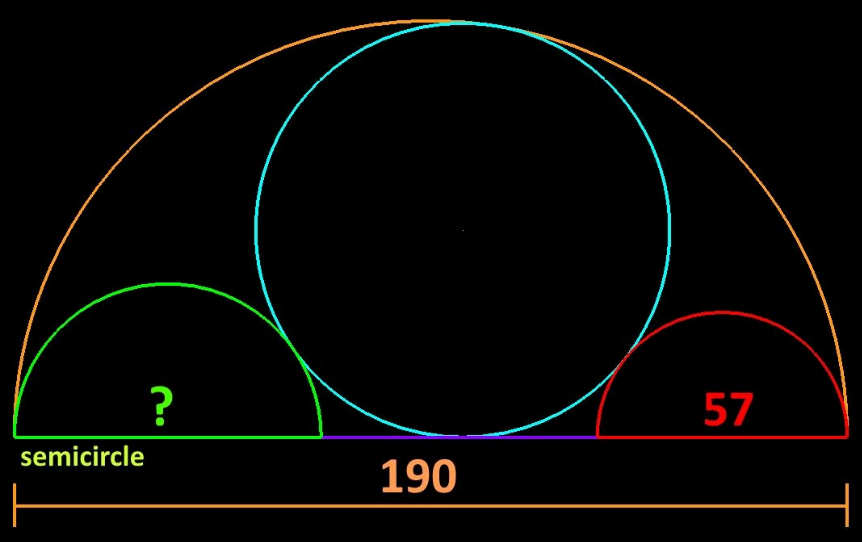
Question Number 185394 Answers: 1 Comments: 0

Question Number 185387 Answers: 2 Comments: 0

Question Number 185386 Answers: 0 Comments: 1

Question Number 185385 Answers: 0 Comments: 0

Question Number 185384 Answers: 1 Comments: 0

Question Number 185383 Answers: 0 Comments: 0

lim_(n→+∞) ((((_1 ^n )(_2 ^n )...(_n ^n )))^(1/n) /(e^(n/2) ×n^(−(1/2)) ))=?

$$\underset{\mathrm{n}\rightarrow+\infty} {\mathrm{lim}}\frac{\sqrt[{\mathrm{n}}]{\left(_{\mathrm{1}} ^{\mathrm{n}} \right)\left(_{\mathrm{2}} ^{\mathrm{n}} \right)...\left(_{\mathrm{n}} ^{\mathrm{n}} \right)}}{\mathrm{e}^{\frac{\mathrm{n}}{\mathrm{2}}} ×\mathrm{n}^{−\frac{\mathrm{1}}{\mathrm{2}}} }=? \\ $$

Question Number 185378 Answers: 0 Comments: 0

Question Number 185374 Answers: 1 Comments: 0

lim_(z→∞) ((iz^3 +iz−1)/((2z+3i)(z−i)^2 )) M.m

$$\mathrm{li}\underset{\mathrm{z}\rightarrow\infty} {\mathrm{m}}\frac{\mathrm{iz}^{\mathrm{3}} +\mathrm{iz}−\mathrm{1}}{\left(\mathrm{2z}+\mathrm{3i}\right)\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 185372 Answers: 2 Comments: 0

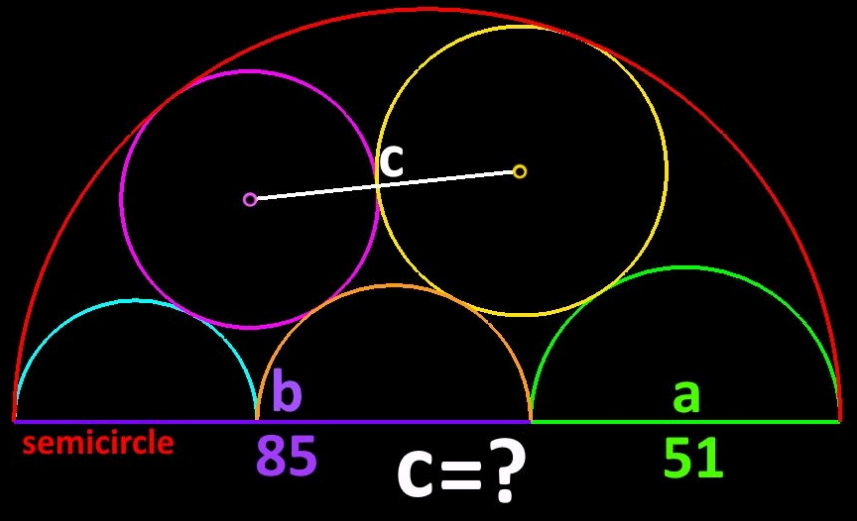
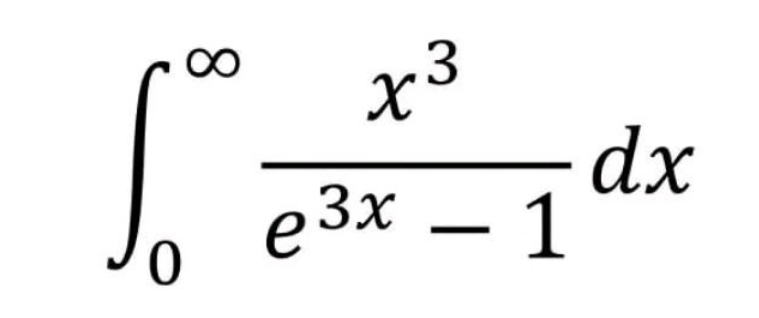
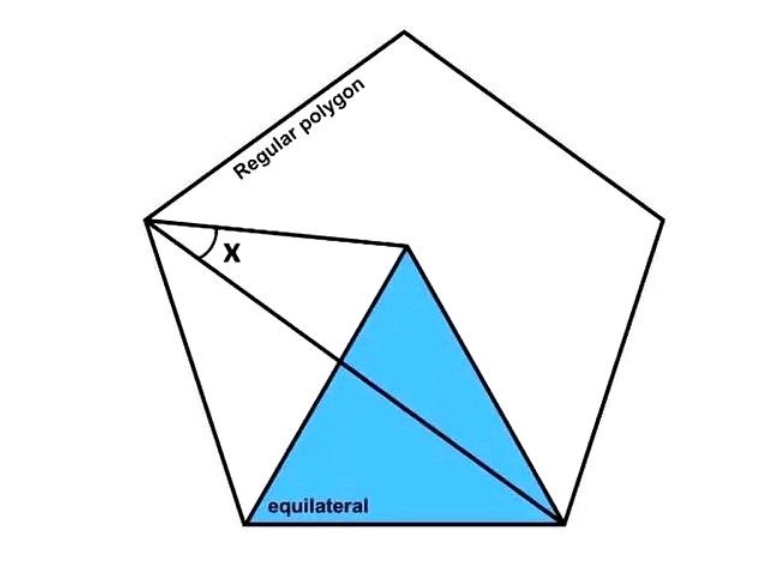
Question Number 185371 Answers: 1 Comments: 0

(1−z)(1−z^− ) = ? Where z is the complex number .

$$\left(\mathrm{1}−\mathrm{z}\right)\left(\mathrm{1}−\overset{−} {\mathrm{z}}\right)\:=\:? \\ $$$$\mathrm{Where}\:\mathrm{z}\:\mathrm{is}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{number} \\ $$$$ \\ $$$$. \\ $$

Question Number 185884 Answers: 0 Comments: 0

Question Number 185361 Answers: 1 Comments: 0

Question Number 185354 Answers: 2 Comments: 0

Question Number 185350 Answers: 0 Comments: 1

C_4 ^4 +C_4 ^5 +C_4 ^6 +...+C_4 ^(26) =?

$$\:\:\:{C}_{\mathrm{4}} ^{\mathrm{4}} +{C}_{\mathrm{4}} ^{\mathrm{5}} +{C}_{\mathrm{4}} ^{\mathrm{6}} +...+{C}_{\mathrm{4}} ^{\mathrm{26}} \:=? \\ $$

Question Number 185348 Answers: 1 Comments: 0

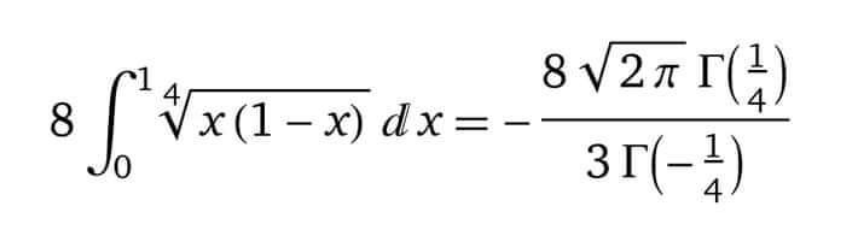
Question Number 185743 Answers: 0 Comments: 0

Question Number 185346 Answers: 0 Comments: 0

Question Number 185337 Answers: 1 Comments: 0

Question Number 185336 Answers: 0 Comments: 0

Question Number 185330 Answers: 1 Comments: 0

what is the difference between d^2 x and (dx)^2

$${what}\:{is}\:{the}\:{difference}\:{between} \\ $$$${d}^{\mathrm{2}} {x}\:{and}\:\left({dx}\right)^{\mathrm{2}} \\ $$

Question Number 185329 Answers: 2 Comments: 0

lim_(k→+∞) Σ_(i=1) ^k (1/( (√(i−1))+(√i)))=

$${lim}_{{k}\rightarrow+\infty} \underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}−\mathrm{1}}+\sqrt{{i}}}= \\ $$

Pg 361 Pg 362 Pg 363 Pg 364 Pg 365 Pg 366 Pg 367 Pg 368 Pg 369 Pg 370

Terms of Service

Contact: info@tinkutara.com