Question and Answers Forum

All Questions   Topic List

AllQuestion and Answers: Page 358

Question Number 183031    Answers: 1   Comments: 0

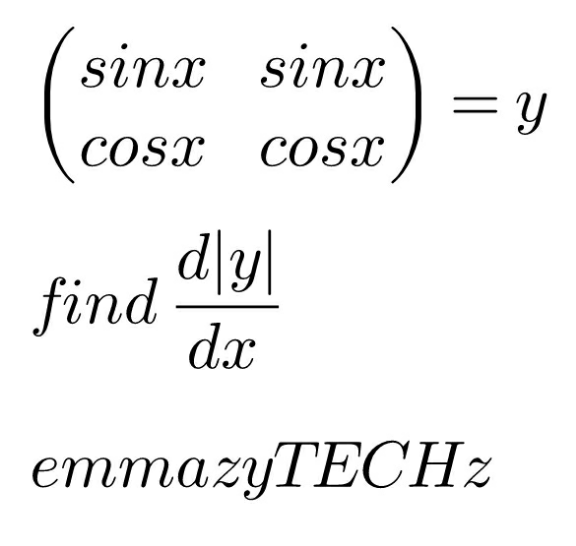
Question Number 183019    Answers: 3   Comments: 2

Q f(x)=a^x +b^x g(x)=((f(x))/(f(x−2))) g(3)=?

$${Q}\:\:\:{f}\left({x}\right)={a}^{{x}} +{b}^{{x}} \:\:\:\:\:{g}\left({x}\right)=\frac{{f}\left({x}\right)}{{f}\left({x}−\mathrm{2}\right)} \\ $$$${g}\left(\mathrm{3}\right)=? \\ $$$$ \\ $$

Question Number 182999    Answers: 1   Comments: 0

(√(m^2 −4m+4)) + ((m−2n+8))^(1/4) = 0 n = ?

$$\sqrt{\mathrm{m}^{\mathrm{2}} −\mathrm{4m}+\mathrm{4}}\:+\:\sqrt[{\mathrm{4}}]{\mathrm{m}−\mathrm{2n}+\mathrm{8}}\:=\:\mathrm{0} \\ $$$$\mathrm{n}\:=\:? \\ $$

Question Number 182998    Answers: 0   Comments: 0

Question Number 182997    Answers: 0   Comments: 0

Question Number 182996    Answers: 0   Comments: 0

Question Number 182995    Answers: 1   Comments: 0

Question Number 182984    Answers: 2   Comments: 0

Find the equation for the plane through the point A(6, 2, −4), B(−2, 4, 8), C(4, −2, 2). −Vector Analysis M.m

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{for}\:\mathrm{the}\:\mathrm{plane} \\ $$$$\mathrm{through}\:\mathrm{the}\:\mathrm{point}\:\mathrm{A}\left(\mathrm{6},\:\mathrm{2},\:−\mathrm{4}\right), \\ $$$$\mathrm{B}\left(−\mathrm{2},\:\mathrm{4},\:\mathrm{8}\right),\:\mathrm{C}\left(\mathrm{4},\:−\mathrm{2},\:\mathrm{2}\right).\:−\mathrm{Vector}\:\mathrm{Analysis} \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 182978    Answers: 2   Comments: 0

Question Number 183008    Answers: 0   Comments: 1

Question Number 183010    Answers: 0   Comments: 10

what is the formula between actual depth apparent depth and refraction index that an object is in a rarer medium?

$${what}\:{is}\:{the}\:{formula}\:{between}\:{actual}\:{depth} \\ $$$${apparent}\:{depth}\:{and}\:{refraction}\:{index} \\ $$$${that}\:{an}\:{object}\:{is}\:{in}\:{a}\:{rarer}\:{medium}? \\ $$

Question Number 182973    Answers: 3   Comments: 0

Question Number 182968    Answers: 0   Comments: 0

Question Number 182965    Answers: 0   Comments: 0

Question Number 182962    Answers: 2   Comments: 0

Question Number 182954    Answers: 0   Comments: 1

I=∫ (1/( (√(x (√x) −x^2 )))) dx I=∫ (1/( ∙ (√(x((√x) −x))))) dx I=∫ (1/( (√x) ∙ (√((√x) −x)) )) ×(2/2) dx I= ∫ (1/( (√(4(√x) −4x)))) ∙ (2/( (√x))) dx I=2∫ ( /( (√(1−(1−2 (√x))^2 )))) ∙ (1/( (√x))) dx I= −2∫ (1/( (√(1−(1−2(√x))^2 )))) ∙ d(1−2(√x)) I= −2sin^(−1) (1−2(√x)) +C Gamil AL mansob

$$\:\boldsymbol{{I}}=\int\:\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{{x}}\:\sqrt{\boldsymbol{{x}}}\:−\boldsymbol{{x}}^{\mathrm{2}} }}\:\boldsymbol{{dx}}\: \\ $$$$\:\:\boldsymbol{{I}}=\int\:\frac{\mathrm{1}}{\:\:\centerdot\:\:\sqrt{\boldsymbol{{x}}\left(\sqrt{\boldsymbol{{x}}}\:−\boldsymbol{{x}}\right)}}\:\boldsymbol{{dx}} \\ $$$$\:\:\boldsymbol{{I}}=\int\:\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{{x}}}\:\centerdot\:\sqrt{\sqrt{\boldsymbol{{x}}}\:−\boldsymbol{{x}}}\:}\:×\frac{\mathrm{2}}{\mathrm{2}}\:\boldsymbol{{dx}} \\ $$$$\:\boldsymbol{{I}}=\:\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}\sqrt{\boldsymbol{{x}}}\:−\mathrm{4}\boldsymbol{{x}}}}\:\centerdot\:\frac{\mathrm{2}}{\:\sqrt{\boldsymbol{{x}}}}\:\boldsymbol{{dx}} \\ $$$$\:\:\boldsymbol{{I}}=\mathrm{2}\int\:\frac{\:}{\:\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2}\:\sqrt{\boldsymbol{{x}}}\right)^{\mathrm{2}} }}\:\centerdot\:\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{{x}}}}\:\boldsymbol{{dx}}\: \\ $$$$\:\:\boldsymbol{{I}}=\:−\mathrm{2}\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2}\sqrt{\boldsymbol{{x}}}\right)^{\mathrm{2}} }}\:\:\centerdot\:\boldsymbol{{d}}\left(\mathrm{1}−\mathrm{2}\sqrt{\boldsymbol{{x}}}\right) \\ $$$$\:\:\boldsymbol{{I}}=\:−\mathrm{2}\boldsymbol{{sin}}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{2}\sqrt{\boldsymbol{{x}}}\right)\:+\boldsymbol{{C}} \\ $$$$\: \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{Gamil}}\:\boldsymbol{\mathrm{AL}}\:\boldsymbol{\mathrm{mansob}} \\ $$

Question Number 182953    Answers: 0   Comments: 0

H_4 (x)=L_0 (x) x=?

$${H}_{\mathrm{4}} \left({x}\right)={L}_{\mathrm{0}} \left({x}\right)\:\:\:\:\:\:\:{x}=? \\ $$

Question Number 182952    Answers: 1   Comments: 0

what is the probability that at least two from 23 people have birthday at the same day? (an unsolved old question)

$${what}\:{is}\:{the}\:{probability}\:{that}\:{at}\:{least} \\ $$$${two}\:{from}\:\mathrm{23}\:{people}\:{have}\:{birthday}\:{at} \\ $$$${the}\:{same}\:{day}? \\ $$$$ \\ $$$$\left({an}\:{unsolved}\:{old}\:{question}\right) \\ $$

Question Number 182949    Answers: 0   Comments: 0

if z(z^2 +3x)+xy=0 show that (d^2 z/dx^2 )+(d^2 z/dy^2 ) = ((2x(x−1))/((z^2 +3)^3 ))

$$\mathrm{if}\:\mathrm{z}\left(\mathrm{z}^{\mathrm{2}} +\mathrm{3x}\right)+\mathrm{xy}=\mathrm{0}\:\mathrm{show}\:\mathrm{that} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{z}}{\mathrm{dx}^{\mathrm{2}} }+\frac{\mathrm{d}^{\mathrm{2}} \mathrm{z}}{\mathrm{dy}^{\mathrm{2}} }\:=\:\frac{\mathrm{2x}\left(\mathrm{x}−\mathrm{1}\right)}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{3}} } \\ $$

Question Number 182947    Answers: 1   Comments: 1

If a< b<0, then ∣a−b∣ + ∣a+b∣ + ∣ab∣=

$$\mathrm{If}\:\:\mathrm{a}<\:\mathrm{b}<\mathrm{0},\:\:\mathrm{then}\:\:\mid\mathrm{a}−\mathrm{b}\mid\:+\:\mid\mathrm{a}+\mathrm{b}\mid\:+\:\mid\mathrm{ab}\mid= \\ $$

Question Number 182946    Answers: 1   Comments: 1

If 0 < x <1 , then ∣ x −1 ∣ + ∣2x−4∣ + ∣2x+1∣=

$$\mathrm{If}\:\:\mathrm{0}\:<\:\mathrm{x}\:<\mathrm{1}\:,\:\:\mathrm{then}\:\:\mid\:\mathrm{x}\:−\mathrm{1}\:\mid\:+\:\mid\mathrm{2x}−\mathrm{4}\mid\:+\:\mid\mathrm{2x}+\mathrm{1}\mid= \\ $$

Question Number 182941    Answers: 0   Comments: 0

Solve: [x^2 +(xy^2 )^(1/3) ](dy/dx)=y M.m

$$\mathrm{Solve}: \\ $$$$\left[\mathrm{x}^{\mathrm{2}} +\left(\mathrm{xy}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right]\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{y} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 182940    Answers: 2   Comments: 0

Are Σ_(n≥1) (1/(4n^2 −1)) and Σ_(n≥1) (1/(n(n+1)(n+2))) convergent?

$${Are}\:\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}}\:{and}\: \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\:\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:\:{convergent}? \\ $$

Question Number 182936    Answers: 0   Comments: 0

$$ \\ $$

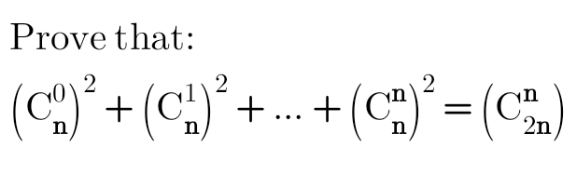
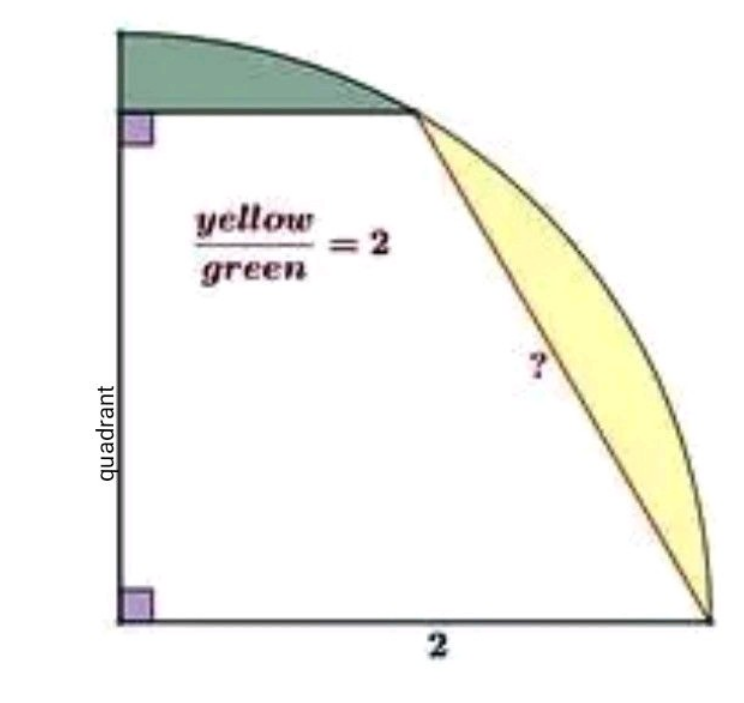
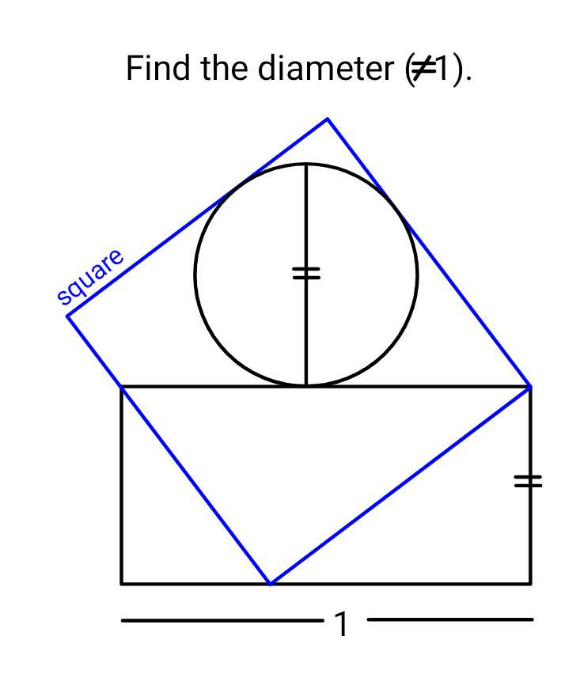
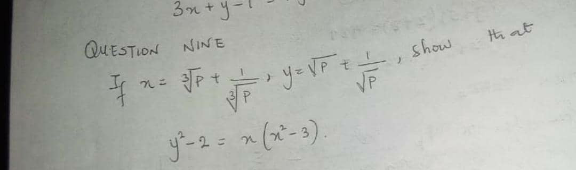
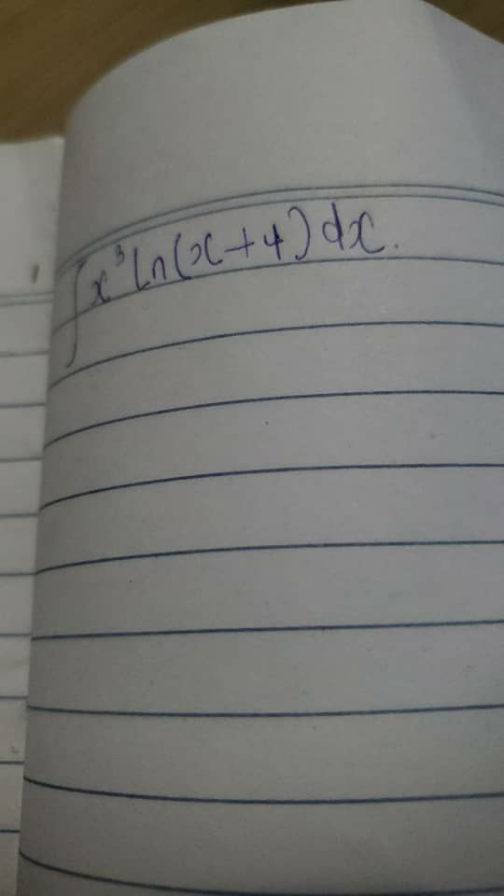
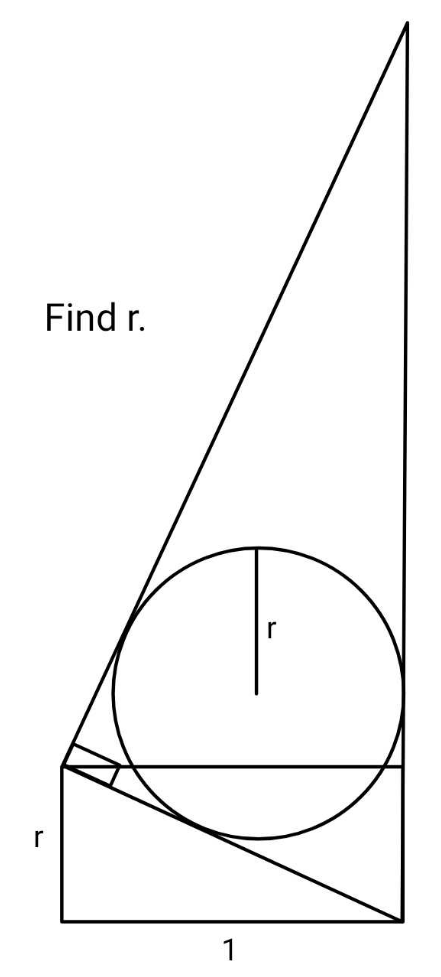
Question Number 182934    Answers: 1   Comments: 0

Is that right ! IF : Σ_(k = 1) ^n (⌊(n/k)⌋−⌊((n−1)/k)⌋) = 2 so n is a prime number .

$$\:\:\:\:\:\:\:\:{Is}\:{that}\:{right}\:! \\ $$$$\:\:\:\:{IF}\:\::\: \\ $$$$\underset{{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\:\left(\lfloor\frac{{n}}{{k}}\rfloor−\lfloor\frac{{n}−\mathrm{1}}{{k}}\rfloor\right)\:=\:\mathrm{2} \\ $$$$\:\:\:{so}\:{n}\:{is}\:{a}\:{prime}\:{number}\:. \\ $$

Question Number 182928    Answers: 6   Comments: 0

  Pg 353      Pg 354      Pg 355      Pg 356      Pg 357      Pg 358      Pg 359      Pg 360      Pg 361      Pg 362   

Terms of Service

Privacy Policy

Contact: info@tinkutara.com