Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 354

Question Number 186739 Answers: 1 Comments: 0

((5+((5+((5+...))^(1/3) ))^(1/3) ))^(1/3) =?

$$\sqrt[{\mathrm{3}}]{\mathrm{5}+\sqrt[{\mathrm{3}}]{\mathrm{5}+\sqrt[{\mathrm{3}}]{\mathrm{5}+...}}}=? \\ $$

Question Number 186737 Answers: 1 Comments: 1

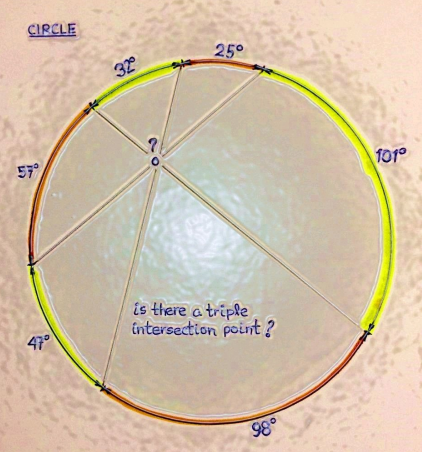
Question Number 186736 Answers: 1 Comments: 0

Question Number 186735 Answers: 1 Comments: 0

Question Number 186726 Answers: 2 Comments: 0

Question Number 186721 Answers: 1 Comments: 1

Question Number 186705 Answers: 1 Comments: 1

a,b>0 , a+b=2 Prove that a^(2b) +b^(2a) +(((a−b)/2))^2 ≤2

$$\mathrm{a},\mathrm{b}>\mathrm{0}\:,\:\mathrm{a}+\mathrm{b}=\mathrm{2} \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{a}^{\mathrm{2b}} +\mathrm{b}^{\mathrm{2a}} +\left(\frac{\mathrm{a}−\mathrm{b}}{\mathrm{2}}\right)^{\mathrm{2}} \leqslant\mathrm{2} \\ $$

Question Number 186701 Answers: 2 Comments: 2

Question Number 186698 Answers: 0 Comments: 0

Question Number 186697 Answers: 2 Comments: 0

Question Number 186692 Answers: 1 Comments: 1

Question Number 186691 Answers: 1 Comments: 0

Question Number 186690 Answers: 1 Comments: 0

Question Number 186689 Answers: 1 Comments: 1

Σ_(n=o) ^(+oo) (x^(3n) /((2n)!)) = ?

$$\underset{{n}={o}} {\overset{+{oo}} {\sum}}\:\frac{{x}^{\mathrm{3}{n}} }{\left(\mathrm{2}{n}\right)!}\:\:=\:\:\:? \\ $$

Question Number 186688 Answers: 0 Comments: 1

a_1 =0 a_2 =1 a_(n+2) =a_(n+1) −a_n a_(885) =?

$${a}_{\mathrm{1}} =\mathrm{0} \\ $$$${a}_{\mathrm{2}} =\mathrm{1} \\ $$$${a}_{{n}+\mathrm{2}} ={a}_{{n}+\mathrm{1}} −{a}_{{n}} \\ $$$${a}_{\mathrm{885}} =? \\ $$

Question Number 186685 Answers: 1 Comments: 0

(sinx)^2 −(1/2)sin2x−2(cosx)^2 ≥0 x∈[0;2π]

$$\left(\mathrm{sin}{x}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2}{x}−\mathrm{2}\left(\mathrm{cos}{x}\right)^{\mathrm{2}} \geq\mathrm{0} \\ $$$${x}\in\left[\mathrm{0};\mathrm{2}\pi\right] \\ $$

Question Number 186682 Answers: 0 Comments: 0

Prove the following set identities 1) A∪(B∪C)=(A∪B)∪C 2) A∪∅=A 3) A∩(B∪C)=(A∩B)∪(A∩C)

$$\mathrm{Prove}\:\mathrm{the}\:\mathrm{following}\:\mathrm{set}\:\mathrm{identities} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{A}\cup\left(\mathrm{B}\cup\mathrm{C}\right)=\left(\mathrm{A}\cup\mathrm{B}\right)\cup\mathrm{C} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{A}\cup\varnothing=\mathrm{A} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{A}\cap\left(\mathrm{B}\cup\mathrm{C}\right)=\left(\mathrm{A}\cap\mathrm{B}\right)\cup\left(\mathrm{A}\cap\mathrm{C}\right) \\ $$

Question Number 186681 Answers: 0 Comments: 0

Etudier la convergence uniforme Σ_(n=0) ^(+∞) (−)^n (e^(−nx^2 ) /((1+n)^3 )) ; n ∈ N.

$${Etudier}\:{la}\:{convergence}\:{uniforme} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\left(−\right)^{{n}} \frac{{e}^{−{nx}^{\mathrm{2}} } }{\left(\mathrm{1}+{n}\right)^{\mathrm{3}} }\:;\:{n}\:\in\:\mathbb{N}. \\ $$

Question Number 186680 Answers: 0 Comments: 0

study the convergence of: Σ_(n=1) ^(+∞) Π_(k=1) ^n (1−e^(((1/k))) )

$${study}\:{the}\:{convergence}\:{of}: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}−{e}^{\left(\frac{\mathrm{1}}{{k}}\right)} \right) \\ $$

Question Number 186667 Answers: 2 Comments: 0

Question Number 186666 Answers: 0 Comments: 0

a,b>0 , a+b=2 Prove that a^(2b) +b^(2a) +(((a−b)/2))^2 ≤2

Question Number 186675 Answers: 2 Comments: 0

Question Number 186662 Answers: 1 Comments: 0

Question Number 186659 Answers: 0 Comments: 1

find the value a and b if lim_(x→0) (((sin 2x)/x^2 ) +a+(b/x^2 ))=0

$${find}\:{the}\:{value}\:{a}\:{and}\:{b}\:{if}\: \\ $$$$\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:\mathrm{2}{x}}{{x}^{\mathrm{2}} }\:+{a}+\frac{{b}}{{x}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$

Question Number 186732 Answers: 2 Comments: 0

Question Number 186657 Answers: 1 Comments: 0

Pg 349 Pg 350 Pg 351 Pg 352 Pg 353 Pg 354 Pg 355 Pg 356 Pg 357 Pg 358

Contact: [email protected]