Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 353

Question Number 185371 Answers: 1 Comments: 0

(1−z)(1−z^− ) = ? Where z is the complex number .

$$\left(\mathrm{1}−\mathrm{z}\right)\left(\mathrm{1}−\overset{−} {\mathrm{z}}\right)\:=\:? \\ $$$$\mathrm{Where}\:\mathrm{z}\:\mathrm{is}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{number} \\ $$$$ \\ $$$$. \\ $$

Question Number 185884 Answers: 0 Comments: 0

Question Number 185361 Answers: 1 Comments: 0

Question Number 185354 Answers: 2 Comments: 0

Question Number 185350 Answers: 0 Comments: 1

C_4 ^4 +C_4 ^5 +C_4 ^6 +...+C_4 ^(26) =?

$$\:\:\:{C}_{\mathrm{4}} ^{\mathrm{4}} +{C}_{\mathrm{4}} ^{\mathrm{5}} +{C}_{\mathrm{4}} ^{\mathrm{6}} +...+{C}_{\mathrm{4}} ^{\mathrm{26}} \:=? \\ $$

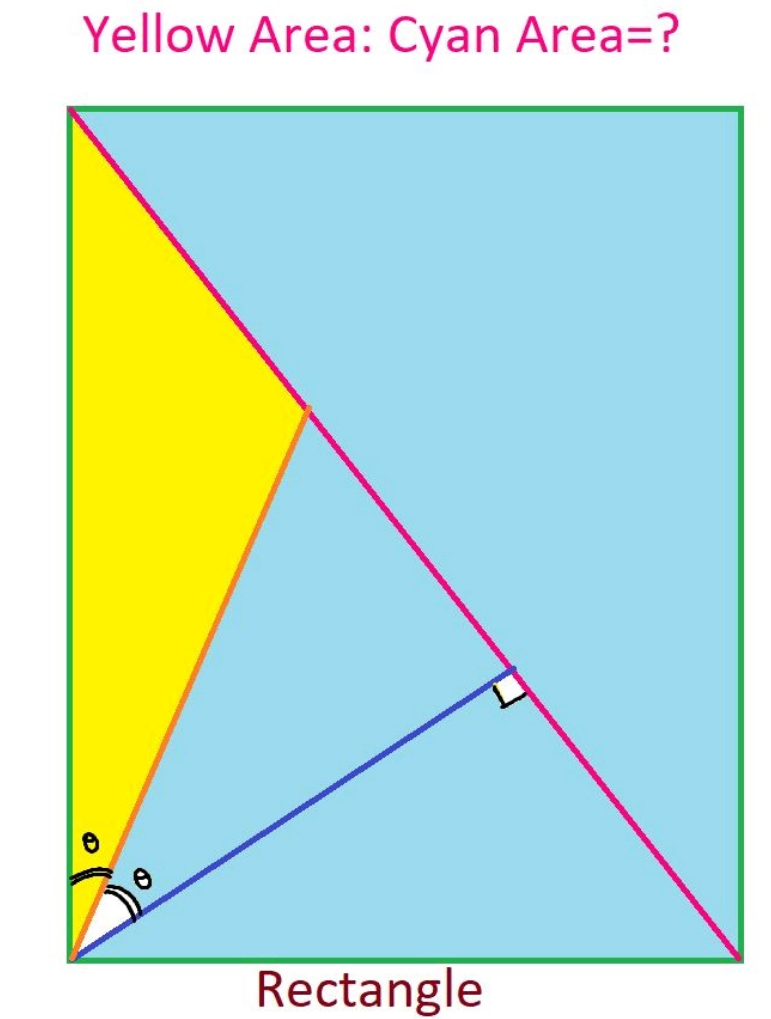
Question Number 185348 Answers: 1 Comments: 0

Question Number 185743 Answers: 0 Comments: 0

Question Number 185346 Answers: 0 Comments: 0

Question Number 185337 Answers: 1 Comments: 0

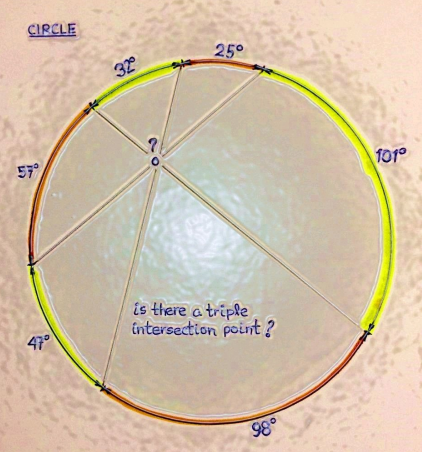
Question Number 185336 Answers: 0 Comments: 0

Question Number 185330 Answers: 1 Comments: 0

what is the difference between d^2 x and (dx)^2

$${what}\:{is}\:{the}\:{difference}\:{between} \\ $$$${d}^{\mathrm{2}} {x}\:{and}\:\left({dx}\right)^{\mathrm{2}} \\ $$

Question Number 185329 Answers: 2 Comments: 0

lim_(k→+∞) Σ_(i=1) ^k (1/( (√(i−1))+(√i)))=

$${lim}_{{k}\rightarrow+\infty} \underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}−\mathrm{1}}+\sqrt{{i}}}= \\ $$

Question Number 185328 Answers: 1 Comments: 0

lim_(k→+∞) Σ_(i=1) ^k (1/( (√i)))=

$${lim}_{{k}\rightarrow+\infty} \underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}}}= \\ $$

Question Number 185325 Answers: 2 Comments: 0

Question Number 185324 Answers: 1 Comments: 0

Question Number 185320 Answers: 2 Comments: 0

Question Number 185426 Answers: 1 Comments: 0

Question Number 185424 Answers: 1 Comments: 5

Question Number 185423 Answers: 1 Comments: 0

Σ_(r=1) ^n 3^(r−1) sin^3 ((θ/3^r )) = ?

$$\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{3}^{{r}−\mathrm{1}} {sin}^{\mathrm{3}} \left(\frac{\theta}{\mathrm{3}^{{r}} }\right)\:=\:? \\ $$

Question Number 185422 Answers: 2 Comments: 0

Question Number 185420 Answers: 1 Comments: 1

Question Number 185315 Answers: 2 Comments: 0

Solve the equation: x! = x^2 − 3x + 20

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\mathrm{x}!\:=\:\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{3x}\:+\:\mathrm{20} \\ $$

Question Number 185310 Answers: 1 Comments: 1

Question Number 185294 Answers: 0 Comments: 3

x^2 −2^x = 1 x= ?

$$\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:−\mathrm{2}^{\boldsymbol{\mathrm{x}}} \:=\:\mathrm{1} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{x}}=\:? \\ $$

Question Number 185293 Answers: 1 Comments: 2

Σ_(k=1) ^n (1/( (√(k+n))))

$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{k}+{n}}} \\ $$

Question Number 185284 Answers: 1 Comments: 0

Pg 348 Pg 349 Pg 350 Pg 351 Pg 352 Pg 353 Pg 354 Pg 355 Pg 356 Pg 357

Terms of Service

Contact: info@tinkutara.com