Question and Answers Forum

AllQuestion and Answers: Page 352

Question Number 186171 Answers: 1 Comments: 0

[so easy] ∫ cos^2 (4x) + sin^4 (2x) dx

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\boldsymbol{{so}}\:\boldsymbol{{easy}}\right] \\ $$$$\:\:\:\:\:\:\:\int\:\boldsymbol{{cos}}^{\mathrm{2}} \:\left(\mathrm{4}\boldsymbol{{x}}\right)\:+\:\boldsymbol{{sin}}^{\mathrm{4}} \:\left(\mathrm{2}\boldsymbol{{x}}\right)\:\boldsymbol{{dx}}\:\:\: \\ $$$$ \\ $$

Question Number 186170 Answers: 1 Comments: 0

∫_(−2) ^2 ((tan^(−1) ( 2 − cos (x)) )/(2 + x^2 )) dx

$$ \\ $$$$\:\:\:\:\:\:\underset{−\mathrm{2}} {\overset{\mathrm{2}} {\int}}\:\:\:\:\frac{\boldsymbol{{tan}}^{−\mathrm{1}} \:\left(\:\mathrm{2}\:−\:\boldsymbol{{cos}}\:\left(\boldsymbol{{x}}\right)\right)\:\:\:\:}{\mathrm{2}\:+\:\boldsymbol{{x}}^{\mathrm{2}} }\:\:\boldsymbol{{dx}} \\ $$$$ \\ $$

Question Number 186165 Answers: 1 Comments: 0

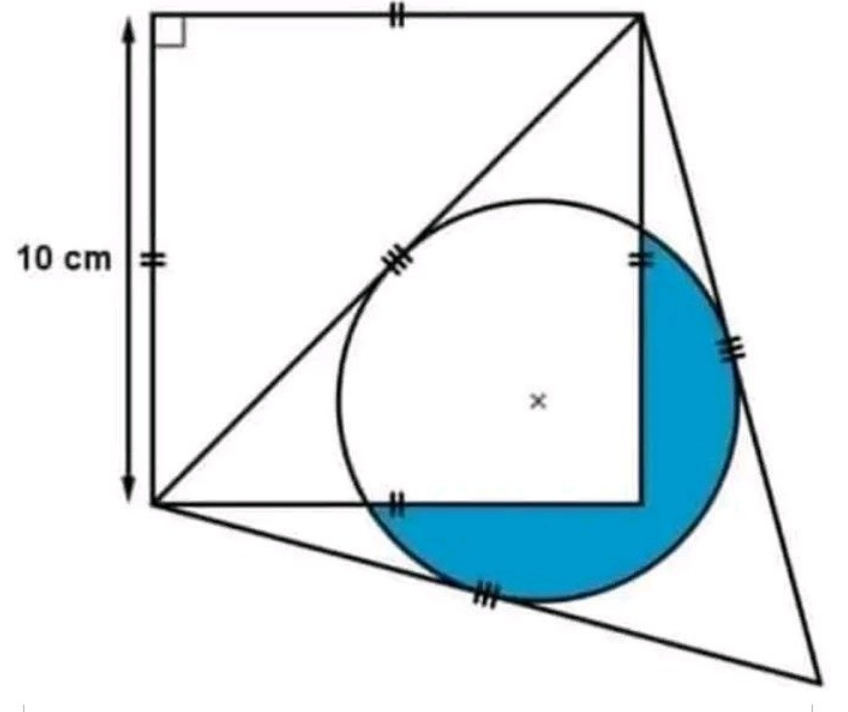
Question Number 186163 Answers: 3 Comments: 0

Question Number 186408 Answers: 1 Comments: 0

Question Number 186152 Answers: 1 Comments: 0

I= ∫_2 ^𝛑 ((cos^2 (x) − 1 )/(1 + sin (x) − tan (x))) dx

$$ \\ $$$$\:\:\:\boldsymbol{{I}}=\:\:\underset{\mathrm{2}} {\overset{\boldsymbol{\pi}} {\int}}\:\:\:\frac{\boldsymbol{{cos}}^{\mathrm{2}} \:\left(\boldsymbol{{x}}\right)\:−\:\mathrm{1}\:}{\mathrm{1}\:+\:\boldsymbol{{sin}}\:\left(\boldsymbol{{x}}\right)\:−\:\boldsymbol{{tan}}\:\left(\boldsymbol{{x}}\right)}\:\:\boldsymbol{{dx}}\:\:\:\: \\ $$$$ \\ $$

Question Number 186146 Answers: 0 Comments: 0

Question Number 186144 Answers: 0 Comments: 9

Question Number 186143 Answers: 2 Comments: 0

Question Number 186142 Answers: 0 Comments: 0

Question Number 186141 Answers: 0 Comments: 1

Question Number 186132 Answers: 1 Comments: 4

Question Number 186126 Answers: 0 Comments: 1

Question Number 186125 Answers: 1 Comments: 0

Question Number 186124 Answers: 1 Comments: 1

Question Number 186123 Answers: 0 Comments: 0

Question Number 186111 Answers: 2 Comments: 2

Question Number 186103 Answers: 0 Comments: 0

Let R denote a set of all ordered pairs (x, y) of integers such that x−y is an integral multiple of 3. Which of the followings ordered pairs belong to R (9,3) (3, 9),( 1 ,2) (1, 5),(7, 2) (0, 4), (4 ,7). (note: a is an integral multiple of b if a=kb where k is an integer)

$$\mathrm{Let}\:\mathrm{R}\:\mathrm{denote}\:\mathrm{a}\:\mathrm{set}\:\mathrm{of}\:\mathrm{all}\:\mathrm{ordered}\:\mathrm{pairs}\:\left(\mathrm{x},\:\mathrm{y}\right)\: \\ $$$$\mathrm{of}\:\mathrm{integers}\:\mathrm{such}\:\mathrm{that}\:\mathrm{x}−\mathrm{y}\:\mathrm{is}\:\mathrm{an}\:\mathrm{integral} \\ $$$$\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{3}.\:\mathrm{Which}\:\mathrm{of}\:\mathrm{the}\:\mathrm{followings}\:\mathrm{ordered}\:\mathrm{pairs} \\ $$$$\mathrm{belong}\:\mathrm{to}\:\mathrm{R}\:\left(\mathrm{9},\mathrm{3}\right)\:\left(\mathrm{3},\:\mathrm{9}\right),\left(\:\mathrm{1}\:,\mathrm{2}\right)\:\left(\mathrm{1},\:\mathrm{5}\right),\left(\mathrm{7},\:\mathrm{2}\right) \\ $$$$\:\left(\mathrm{0},\:\mathrm{4}\right),\:\left(\mathrm{4}\:,\mathrm{7}\right). \\ $$$$\left(\mathrm{note}:\:\mathrm{a}\:\mathrm{is}\:\mathrm{an}\:\mathrm{integral}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{b}\:\mathrm{if}\:\mathrm{a}=\mathrm{kb}\right. \\ $$$$\left.\mathrm{whe}{re}\:\mathrm{k}\:\mathrm{is}\:\mathrm{an}\:\mathrm{integer}\right) \\ $$

Question Number 186105 Answers: 3 Comments: 0

a^2 + 1 = a a^(12) + a^6 + 1 = ?

$$\:{a}^{\mathrm{2}} \:+\:\mathrm{1}\:\:=\:{a} \\ $$$$\:{a}^{\mathrm{12}} \:+\:{a}^{\mathrm{6}} \:+\:\mathrm{1}\:=\:?\: \\ $$

Question Number 186099 Answers: 1 Comments: 0

1. Solve for the linear system: x−2y+3z=5 2x+y−4z=0 3x+4y−11z=−5 2. Ghana railways co−operation has 20 trains for it′s operations. It is observed that x trains can accommodate 2 passengers, y trains 3 passengers and z trains 5 passengers. Howeer, the totsl number of passrngers always present at Ghana railways are 64. During market day, 3 of x trains, 2 of y trains and 4 of z trains for a total of 10 trains were used. Determine the values of x, y and z.

$$\mathrm{1}.\:{Solve}\:{for}\:{the}\:{linear}\:{system}: \\ $$$${x}−\mathrm{2}{y}+\mathrm{3}{z}=\mathrm{5} \\ $$$$\mathrm{2}{x}+{y}−\mathrm{4}{z}=\mathrm{0} \\ $$$$\mathrm{3}{x}+\mathrm{4}{y}−\mathrm{11}{z}=−\mathrm{5} \\ $$$$\mathrm{2}.\:{Ghana}\:{railways}\:{co}−{operation}\:{has}\:\mathrm{20}\: \\ $$$${trains}\:{for}\:{it}'{s}\:{operations}.\:{It}\:{is}\:{observed}\:{that} \\ $$$${x}\:{trains}\:{can}\:{accommodate}\:\mathrm{2}\:{passengers}, \\ $$$${y}\:{trains}\:\mathrm{3}\:{passengers}\:{and}\:{z}\:{trains}\:\mathrm{5}\: \\ $$$${passengers}.\:{Howeer},\:{the}\:{totsl}\:{number}\:{of} \\ $$$${passrngers}\:{always}\:{present}\:{at}\:{Ghana}\: \\ $$$${railways}\:{are}\:\mathrm{64}.\:{During}\:{market}\:{day},\:\mathrm{3}\:{of} \\ $$$${x}\:{trains},\:\mathrm{2}\:{of}\:{y}\:{trains}\:{and}\:\mathrm{4}\:{of}\:{z}\:{trains}\:{for}\: \\ $$$${a}\:{total}\:{of}\:\mathrm{10}\:{trains}\:{were}\:{used}.\:{Determine}\: \\ $$$${the}\:{values}\:{of}\:{x},\:{y}\:{and}\:{z}. \\ $$

Question Number 186094 Answers: 0 Comments: 0

Q1000

$${Q}\mathrm{1000} \\ $$

Question Number 186082 Answers: 0 Comments: 0

Question Number 186080 Answers: 0 Comments: 0

Question Number 186079 Answers: 1 Comments: 0

Question Number 186077 Answers: 1 Comments: 0

Prove that ▽•(∅A^− )=(▽∅)•A+∅(▽•A^− ). Help!

$$\mathrm{Prove}\:\mathrm{that}\: \\ $$$$\bigtriangledown\bullet\left(\varnothing\overset{−} {\mathrm{A}}\right)=\left(\bigtriangledown\varnothing\right)\bullet\mathrm{A}+\varnothing\left(\bigtriangledown\bullet\overset{−} {\mathrm{A}}\right). \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Question Number 186074 Answers: 1 Comments: 0

Prove that div(curlA^− )=0 Help!

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{div}\left(\mathrm{curl}\overset{−} {\mathrm{A}}\right)=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Pg 347 Pg 348 Pg 349 Pg 350 Pg 351 Pg 352 Pg 353 Pg 354 Pg 355 Pg 356

Contact: info@tinkutara.com