
AllQuestion and Answers: Page 350
Question Number 187092 Answers: 2 Comments: 0
Question Number 187091 Answers: 2 Comments: 0
Question Number 187088 Answers: 0 Comments: 1
Question Number 187087 Answers: 0 Comments: 1
Question Number 187086 Answers: 0 Comments: 0

Question Number 187085 Answers: 1 Comments: 0

Question Number 187080 Answers: 0 Comments: 0
Question Number 187076 Answers: 3 Comments: 0
Question Number 187073 Answers: 0 Comments: 0
Question Number 187072 Answers: 0 Comments: 0
Question Number 187069 Answers: 1 Comments: 0
Question Number 187066 Answers: 3 Comments: 1

Question Number 187059 Answers: 1 Comments: 1

Question Number 187054 Answers: 0 Comments: 2

Question Number 187053 Answers: 1 Comments: 0
Question Number 187051 Answers: 0 Comments: 1
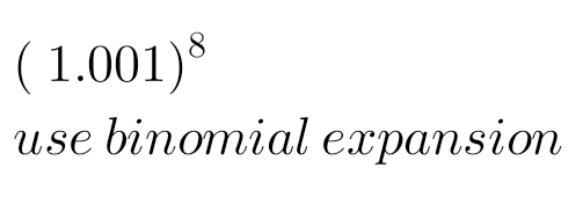
Question Number 187050 Answers: 0 Comments: 1
Question Number 187046 Answers: 1 Comments: 0
Question Number 187029 Answers: 1 Comments: 0

Question Number 187027 Answers: 1 Comments: 0

Question Number 187025 Answers: 1 Comments: 0

Question Number 187044 Answers: 0 Comments: 0
Question Number 187020 Answers: 0 Comments: 1
Question Number 187011 Answers: 0 Comments: 0
Question Number 187010 Answers: 0 Comments: 0
Question Number 187008 Answers: 2 Comments: 0
Pg 345 Pg 346 Pg 347 Pg 348 Pg 349 Pg 350 Pg 351 Pg 352 Pg 353 Pg 354
