Question and Answers Forum

AllQuestion and Answers: Page 348

Question Number 185685 Answers: 1 Comments: 0

Question Number 185684 Answers: 0 Comments: 7

17 , 78, 143, 353, ? a)366 b)0 c)398 d)435

$$\mathrm{17}\:,\:\mathrm{78},\:\mathrm{143},\:\mathrm{353},\:? \\ $$$$\left.\mathrm{a}\left.\right)\left.\mathrm{3}\left.\mathrm{66}\:\:\:\:\:\mathrm{b}\right)\mathrm{0}\:\:\:\:\:\mathrm{c}\right)\mathrm{398}\:\:\:\:\:\mathrm{d}\right)\mathrm{435} \\ $$

Question Number 185678 Answers: 1 Comments: 0

Question Number 185677 Answers: 1 Comments: 0

Question Number 185674 Answers: 1 Comments: 1

Question Number 185673 Answers: 1 Comments: 0

Question Number 185672 Answers: 0 Comments: 0

Question Number 185668 Answers: 2 Comments: 0

Find: (1/(sin 10°)) − 4 sin 70° = ?

$$\mathrm{Find}:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{10}°}\:−\:\mathrm{4}\:\mathrm{sin}\:\mathrm{70}°\:=\:? \\ $$

Question Number 185665 Answers: 1 Comments: 0

f(((2x−1)/(3x+2)))=((x−1)/(x−2)) faind f^(−1) (2)=?

$${f}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{3}{x}+\mathrm{2}}\right)=\frac{{x}−\mathrm{1}}{{x}−\mathrm{2}}\:\:\:\:\:\:{faind}\:\:\:{f}^{−\mathrm{1}} \left(\mathrm{2}\right)=? \\ $$

Question Number 185664 Answers: 0 Comments: 0

Question Number 185663 Answers: 0 Comments: 0

Question Number 185659 Answers: 1 Comments: 1

prove for r, n ∈ N Σ_(k=r) ^n ((k),(r) ) = (((n+1)),((r+1)) ) (Hockey−stick identity)

$${prove}\:{for}\:{r},\:{n}\:\in\:\mathbb{N} \\ $$$$\underset{{k}={r}} {\overset{{n}} {\sum}}\begin{pmatrix}{{k}}\\{{r}}\end{pmatrix}\:=\begin{pmatrix}{{n}+\mathrm{1}}\\{{r}+\mathrm{1}}\end{pmatrix} \\ $$$$\left({Hockey}−{stick}\:{identity}\right) \\ $$

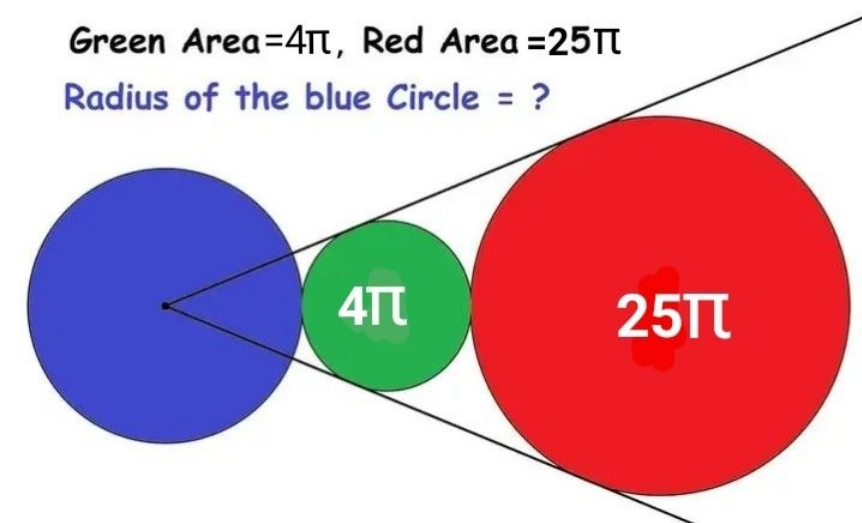
Question Number 185647 Answers: 1 Comments: 0

Question Number 185637 Answers: 1 Comments: 0

Question Number 185642 Answers: 1 Comments: 1

Question Number 185640 Answers: 2 Comments: 0

Question Number 185619 Answers: 1 Comments: 1

Question Number 185719 Answers: 1 Comments: 2

Find the next number: a_0 =a_1 =1, a_2 =2 a_3 =?

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{next}\:\mathrm{number}: \\ $$$${a}_{\mathrm{0}} ={a}_{\mathrm{1}} =\mathrm{1},\:{a}_{\mathrm{2}} =\mathrm{2} \\ $$$${a}_{\mathrm{3}} =? \\ $$

Question Number 185602 Answers: 2 Comments: 0

Question Number 185601 Answers: 0 Comments: 0

Hello please I experienced a little difficulty with this question. A charge Qa =−20mC is located at (−6 4 7) and a charge Qb=50mC at (5 8 −2). If distances are given in meters find (a)R^− ab (b)Rab (c) The vector force exerted on Qa by Qb if ε_0 =10^(−9) /36⊼ F╱m

$${Hello}\:{please}\:{I}\:{experienced}\:{a}\:{little} \\ $$$$\:{difficulty}\:{with}\:{this}\:{question}.\: \\ $$$$ \\ $$$${A}\:{charge}\:{Qa}\:=−\mathrm{20}{mC}\:\:{is}\:{located}\:{at}\:\left(−\mathrm{6}\:\mathrm{4}\:\mathrm{7}\right)\:{and}\: \\ $$$${a}\:{charge}\:{Qb}=\mathrm{50}{mC}\:{at}\:\left(\mathrm{5}\:\mathrm{8}\:−\mathrm{2}\right).\: \\ $$$$\mathrm{I}{f}\:{distances}\:{are}\:{given}\:{in}\:{meters}\: \\ $$$${find}\:\left({a}\right)\overset{−} {{R}ab}\:\left({b}\right){Rab} \\ $$$$\:\left({c}\right)\:{The}\:{vector}\:{force}\:{exerted}\:{on}\: \\ $$$${Qa}\:{by}\:{Qb}\:\:{if}\:\:\varepsilon_{\mathrm{0}} =\mathrm{10}^{−\mathrm{9}} /\mathrm{36}\barwedge\:{F}\diagup{m} \\ $$

Question Number 185599 Answers: 4 Comments: 3

x!=x^3 −x faind x=?

$${x}!={x}^{\mathrm{3}} −{x}\:\:\:\:\:\:\:\:\:\:{faind}\:{x}=? \\ $$

Question Number 185598 Answers: 0 Comments: 0

Question Number 185597 Answers: 0 Comments: 0

Question Number 185596 Answers: 0 Comments: 1

Question Number 185625 Answers: 1 Comments: 0

De^ terminer a, b et c trois termes conse^ quences d′une suite ge^ ometrique tels que: { ((a+b+c=36,75)),((abc=343)) :}

$${D}\acute {{e}terminer}\:{a},\:{b}\:{et}\:{c}\:{trois}\:{termes}\:{cons}\acute {{e}quences} \\ $$$${d}'{une}\:{suite}\:{g}\acute {{e}ometrique}\:{tels}\:{que}: \\ $$$$\begin{cases}{{a}+{b}+{c}=\mathrm{36},\mathrm{75}}\\{{abc}=\mathrm{343}}\end{cases} \\ $$

Question Number 185624 Answers: 1 Comments: 0

Pg 343 Pg 344 Pg 345 Pg 346 Pg 347 Pg 348 Pg 349 Pg 350 Pg 351 Pg 352

Contact: info@tinkutara.com