Question and Answers Forum

AllQuestion and Answers: Page 345

Question Number 184121 Answers: 2 Comments: 4

Question Number 184112 Answers: 1 Comments: 1

∫ (dx/((x−1)^(5/6) (x+2)^(7/6) )) =?

$$\:\:\int\:\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{5}/\mathrm{6}} \left({x}+\mathrm{2}\right)^{\mathrm{7}/\mathrm{6}} }\:=? \\ $$

Question Number 184105 Answers: 2 Comments: 0

We cut a square sheet of metal into equal thirteen cross slices, we measured its perimeter of 168 cm How much was the perimeter of the plate before cutting?

$$\:{We}\:{cut}\:{a}\:{square}\:{sheet}\:{of}\:{metal}\:{into}\:{equal}\:{thirteen} \\ $$$$\:{cross}\:{slices},\:{we}\:{measured}\:{its}\:{perimeter}\:{of}\:\mathrm{168}\:{cm} \\ $$$$\:{How}\:{much}\:{was}\:{the}\:{perimeter}\:{of}\:{the}\:{plate} \\ $$$$\:{before}\:{cutting}? \\ $$

Question Number 184103 Answers: 0 Comments: 0

evaluate ∫_0 ^(𝛑/2) e^(cos(x)) dx

$$\boldsymbol{\mathrm{evaluate}}\:\overset{\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\int}_{\mathrm{0}} \boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)} \boldsymbol{\mathrm{dx}} \\ $$

Question Number 184102 Answers: 1 Comments: 0

∫_0 ^1 ((ln^4 (1−x))/( (√(1−x))))dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}^{\mathrm{4}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)}{\:\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}}}\boldsymbol{\mathrm{dx}} \\ $$

Question Number 184098 Answers: 1 Comments: 2

∫_0 ^1 ((ln^2 (1−x))/(1−x))dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}^{\mathrm{2}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}−\boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{dx}} \\ $$

Question Number 184095 Answers: 2 Comments: 0

Question Number 184093 Answers: 2 Comments: 0

Question Number 184091 Answers: 2 Comments: 1

Question Number 184085 Answers: 1 Comments: 0

(y^2 + xy^2 )y^′ + x^2 − yx^2 = 0

$$\left(\mathrm{y}^{\mathrm{2}} \:+\:\mathrm{xy}^{\mathrm{2}} \right)\mathrm{y}^{'} \:+\:\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{yx}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$ \\ $$

Question Number 184084 Answers: 1 Comments: 0

Question Number 184083 Answers: 1 Comments: 0

f(x)= x^( 3) +3x^( 2) −ax is decreasing on [ −1 , 2] then which is correct... 1: [ −3 ,24] 2: [ 24 , +∞) 3: (−∞ ,−3] 4 :(−∞, −3]∪[24, +∞)

$$ \\ $$$$\:\:\:\:{f}\left({x}\right)=\:{x}^{\:\mathrm{3}} \:+\mathrm{3}{x}^{\:\mathrm{2}} −{ax}\:\:\:{is}\:\: \\ $$$$\:\:\:\:\:{decreasing}\:{on}\:\:\left[\:−\mathrm{1}\:,\:\mathrm{2}\right] \\ $$$$\:\:\:\:\:\:{then}\:\:{which}\:\:{is}\:{correct}... \\ $$$$\:\:\:\:\:\mathrm{1}:\:\:\:\left[\:−\mathrm{3}\:,\mathrm{24}\right] \\ $$$$\:\:\:\:\:\mathrm{2}:\:\:\left[\:\mathrm{24}\:,\:+\infty\right) \\ $$$$\:\:\:\:\:\:\mathrm{3}:\:\left(−\infty\:,−\mathrm{3}\right] \\ $$$$\:\:\:\:\:\:\:\:\mathrm{4}\::\left(−\infty,\:−\mathrm{3}\right]\cup\left[\mathrm{24},\:+\infty\right) \\ $$$$ \\ $$

Question Number 184076 Answers: 0 Comments: 2

6647^3 mod10000=2023

$$\mathrm{6647}^{\mathrm{3}} {mod}\mathrm{10000}=\mathrm{2023} \\ $$

Question Number 184066 Answers: 1 Comments: 0

(dy/dx)=y(y+2). find y=?

$$\frac{{dy}}{{dx}}={y}\left({y}+\mathrm{2}\right).\:{find}\:\:{y}=? \\ $$

Question Number 184062 Answers: 1 Comments: 0

Prove that Σ_(i=1) ^n (1/( (√(i^2 +i)))) > ln(n+1)

$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{\:\sqrt{{i}^{\mathrm{2}} +{i}}}\:>\:\mathrm{ln}\left({n}+\mathrm{1}\right) \\ $$

Question Number 184061 Answers: 1 Comments: 0

∫((sin^(−1) (√x)−cos^(−1) (√x))/(sin^(−1) (√x)+cos^(−1) (√x)))dx=?

$$\int\frac{{sin}^{−\mathrm{1}} \sqrt{{x}}−{cos}^{−\mathrm{1}} \sqrt{{x}}}{{sin}^{−\mathrm{1}} \sqrt{{x}}+{cos}^{−\mathrm{1}} \sqrt{{x}}}{dx}=? \\ $$

Question Number 184048 Answers: 5 Comments: 0

{ ((u_0 = 2)),((u_(n+1) = ((2u_n −1)/u_n ))) :} Find u_n .

$$\:\:\begin{cases}{{u}_{\mathrm{0}} \:=\:\mathrm{2}}\\{{u}_{{n}+\mathrm{1}} \:=\:\frac{\mathrm{2}{u}_{{n}} \:−\mathrm{1}}{{u}_{{n}} }}\end{cases} \\ $$$$\:\:\:{Find}\:{u}_{{n}} . \\ $$

Question Number 184041 Answers: 2 Comments: 0

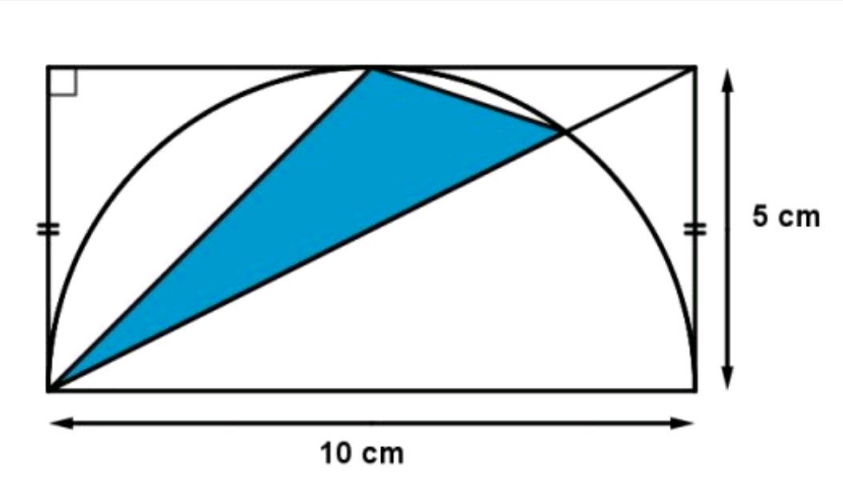
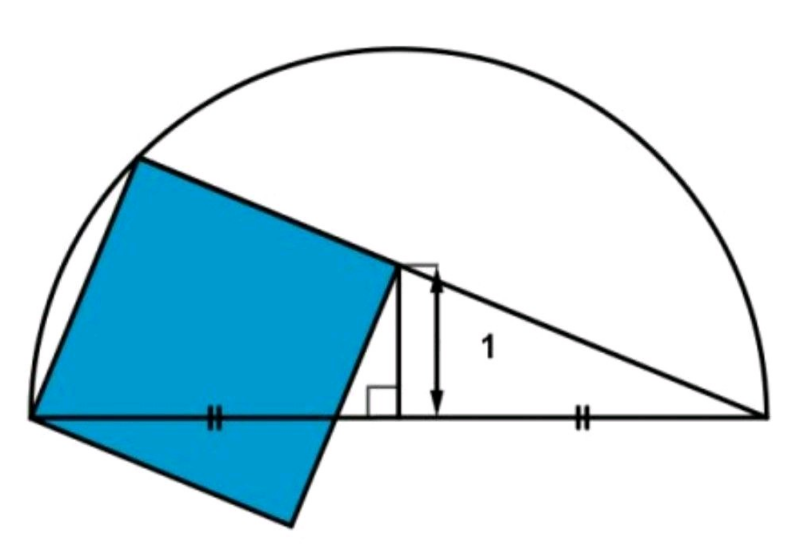
Question Number 184040 Answers: 4 Comments: 0

Use implicit differentiation to find (d^2 y/dx^2 ) for siny = x

$$\mathrm{Use}\:\mathrm{implicit}\:\mathrm{differentiation}\:\mathrm{to}\:\mathrm{find}\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} } \\ $$$$\mathrm{for}\:\mathrm{sin}{y}\:=\:{x} \\ $$

Question Number 184037 Answers: 2 Comments: 0

i^2 =−1 Σ_(j=1) ^(2023) ji^j =?

$${i}^{\mathrm{2}} =−\mathrm{1} \\ $$$$\underset{{j}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}{ji}^{{j}} =? \\ $$

Question Number 184030 Answers: 1 Comments: 0

How many words can be made from 5 letters if (a) all letters are different (b) 2 letters are identical (c) all letters are different but 2 partucular letters cannot be adjacent. M.m

$$\mathrm{How}\:\mathrm{many}\:\mathrm{words}\:\mathrm{can}\:\mathrm{be}\:\mathrm{made}\: \\ $$$$\mathrm{from}\:\mathrm{5}\:\mathrm{letters}\:\mathrm{if} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{all}\:\mathrm{letters}\:\mathrm{are}\:\mathrm{different} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{2}\:\mathrm{letters}\:\mathrm{are}\:\mathrm{identical} \\ $$$$\left(\mathrm{c}\right)\:\mathrm{all}\:\mathrm{letters}\:\mathrm{are}\:\mathrm{different}\:\mathrm{but}\:\mathrm{2} \\ $$$$\mathrm{partucular}\:\mathrm{letters}\:\mathrm{cannot}\:\mathrm{be} \\ $$$$\mathrm{adjacent}. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 184029 Answers: 1 Comments: 0

∫_0 ^( 1) (( x−1)/(x+1))∙(1/(ln(x))) dx =?

$$\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\boldsymbol{\mathrm{x}}−\mathrm{1}}{\boldsymbol{\mathrm{x}}+\mathrm{1}}\centerdot\frac{\mathrm{1}}{\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)}\:\boldsymbol{\mathrm{dx}}\:=? \\ $$

Question Number 184028 Answers: 0 Comments: 0

H^(A^P P) Y Y_(E_A R) ! ⌊e⌋⌊i-i⌋⌊e⌋⌊𝛑⌋^(−)

Question Number 184027 Answers: 1 Comments: 0

∫_0 ^( (𝛑/2)) e^(−tg^2 (x)) dx = ???

$$\:\:\: \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \:\boldsymbol{\mathrm{e}}^{−\boldsymbol{{tg}}^{\mathrm{2}} \left(\boldsymbol{{x}}\right)} \:\boldsymbol{{d}\mathrm{x}}\:=\:??? \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Question Number 184019 Answers: 1 Comments: 2

{ ((y^x = 64)),((y^((x + 1)/(x − 1)) = 16)) :} find “x”

$$\begin{cases}{{y}^{{x}} =\:\mathrm{64}}\\{{y}^{\frac{{x}\:+\:\mathrm{1}}{{x}\:−\:\mathrm{1}}} \:=\:\mathrm{16}}\end{cases} \\ $$$$\:{find}\:``{x}'' \\ $$

Question Number 184018 Answers: 1 Comments: 0

evaluate 𝚺_(n=1) ^∞ (1/(n^3 (((6n)),((3n)) )))

$$\boldsymbol{\mathrm{evaluate}}\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\boldsymbol{\sum}}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}^{\mathrm{3}} \begin{pmatrix}{\mathrm{6}\boldsymbol{\mathrm{n}}}\\{\mathrm{3}\boldsymbol{\mathrm{n}}}\end{pmatrix}} \\ $$

Pg 340 Pg 341 Pg 342 Pg 343 Pg 344 Pg 345 Pg 346 Pg 347 Pg 348 Pg 349

Contact: info@tinkutara.com