Question and Answers Forum

AllQuestion and Answers: Page 337

Question Number 188407 Answers: 3 Comments: 0

xf(x) = f(x + 2) f(2) = 2 f(8) = ?

$${xf}\left({x}\right)\:=\:{f}\left({x}\:+\:\mathrm{2}\right) \\ $$$${f}\left(\mathrm{2}\right)\:=\:\mathrm{2} \\ $$$${f}\left(\mathrm{8}\right)\:=\:?\: \\ $$

Question Number 188503 Answers: 0 Comments: 0

Question Number 188392 Answers: 2 Comments: 3

Question Number 188387 Answers: 2 Comments: 0

Question Number 188384 Answers: 1 Comments: 0

if ∫_0 ^∞ e^(−ax) dx = (1/a) show that ∫_0 ^∞ e^(−ax) x^n dx = ((n!)/a^(n+1) )

$$\:\:\: \\ $$$$\:\:\:\mathrm{if}\:\:\:\:\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} {dx}\:\:=\:\:\frac{\mathrm{1}}{{a}} \\ $$$$\:\:\:\:\:\:\:\:{show}\:{that}\:\:\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} \:{x}^{{n}} {dx}\:\:=\:\:\frac{{n}!}{{a}^{{n}+\mathrm{1}} } \\ $$

Question Number 188381 Answers: 2 Comments: 0

Advanced calculus Find the value of the following series. Ω = Σ_(n=1) ^∞ (( (−1)^( n) ζ ( n ))/(n. 2^( n) )) = ? ζ ( z ) = Σ_( n=1) ^∞ (( 1)/(n^( z) )) ; Re ( z )>1

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{Advanced}\:\:\mathrm{calculus} \\ $$$$ \\ $$$$\:\:\:\:\:\mathrm{Find}\:\:\mathrm{the}\:\:\mathrm{value}\:\:\mathrm{of}\:\mathrm{the}\:\mathrm{following}\:\mathrm{series}. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\Omega\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\:\left(−\mathrm{1}\right)^{\:{n}} \:\zeta\:\left(\:{n}\:\right)}{{n}.\:\mathrm{2}^{\:{n}} }\:=\:? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\zeta\:\left(\:{z}\:\right)\:=\:\underset{\:{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\mathrm{1}}{{n}^{\:{z}} \:}\:\:\:\:\:;\:\:\:\:\mathscr{R}{e}\:\left(\:{z}\:\right)>\mathrm{1} \\ $$$$ \\ $$

Question Number 188380 Answers: 1 Comments: 0

Question Number 188379 Answers: 0 Comments: 0

Question Number 188378 Answers: 1 Comments: 0

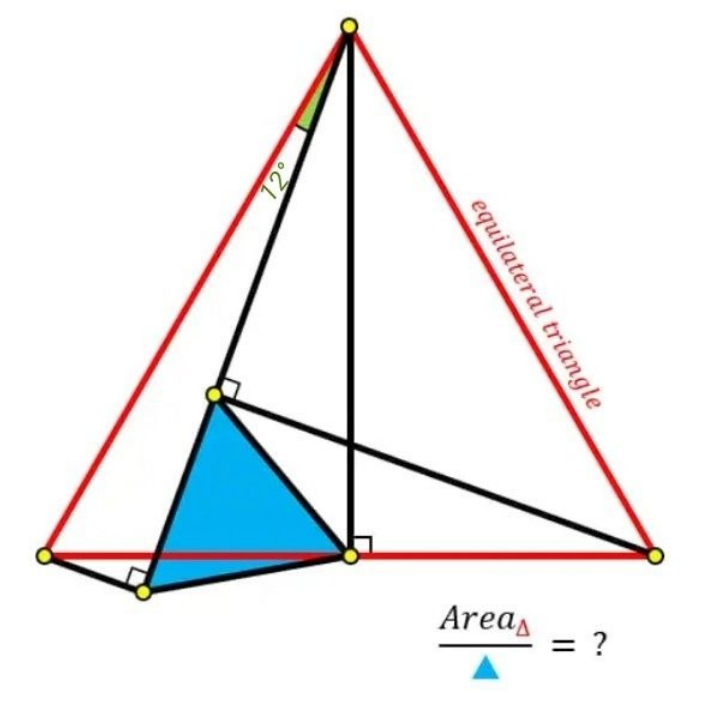
Question Number 188377 Answers: 0 Comments: 0

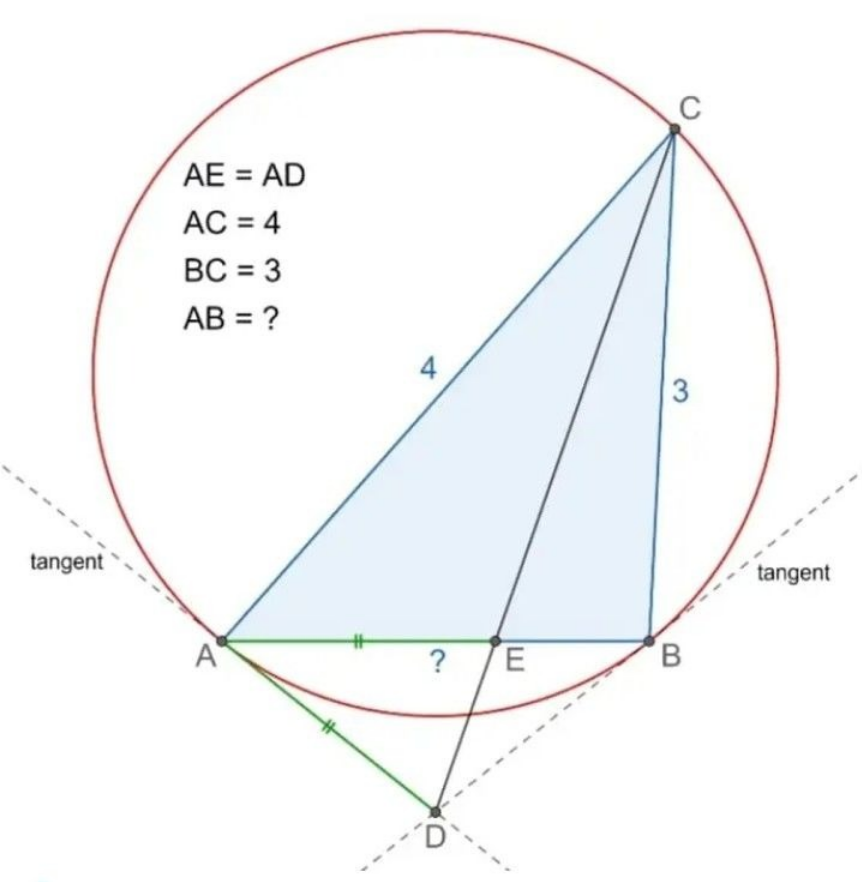
Question Number 188376 Answers: 1 Comments: 0

Question Number 188375 Answers: 1 Comments: 2

Question Number 188374 Answers: 0 Comments: 0

Question Number 189462 Answers: 0 Comments: 0

Question Number 188366 Answers: 1 Comments: 0

xlnx=7 x?

$${xlnx}=\mathrm{7}\:\:\:\:\: \\ $$$${x}? \\ $$

Question Number 188362 Answers: 2 Comments: 0

find the number of 5 digit natural numbers with strictly ascending digits whose sum is 20. example: 12458 is such a number

$${find}\:{the}\:{number}\:{of}\:\mathrm{5}\:{digit}\:{natural} \\ $$$${numbers}\:{with}\:{strictly}\:{ascending}\: \\ $$$${digits}\:{whose}\:{sum}\:{is}\:\mathrm{20}. \\ $$$${example}:\:\mathrm{12458}\:{is}\:{such}\:{a}\:{number} \\ $$

Question Number 188360 Answers: 2 Comments: 0

Question Number 188359 Answers: 1 Comments: 0

Question Number 188351 Answers: 2 Comments: 0

(√x)+(√(3x−2))=x^2 +1

$$\sqrt{{x}}+\sqrt{\mathrm{3}{x}−\mathrm{2}}={x}^{\mathrm{2}} +\mathrm{1} \\ $$

Question Number 188348 Answers: 0 Comments: 1

Question Number 188536 Answers: 2 Comments: 0

solve the equation; {: ((x + y − z =5)),((z − yx = 7)),((z = 1 + x)) } x;y;z =??

$$ \\ $$$$\:\:\:\:\boldsymbol{{solve}}\:\boldsymbol{{the}}\:\boldsymbol{{equation}}; \\ $$$$\:\:\:\:\:\:\:\left.\begin{matrix}{\boldsymbol{{x}}\:+\:\boldsymbol{{y}}\:−\:\boldsymbol{{z}}\:=\mathrm{5}}\\{\boldsymbol{{z}}\:−\:\boldsymbol{{yx}}\:=\:\mathrm{7}}\\{\boldsymbol{{z}}\:=\:\mathrm{1}\:+\:\boldsymbol{{x}}}\end{matrix}\right\}\:\:\boldsymbol{{x}};\boldsymbol{{y}};\boldsymbol{{z}}\:=??\:\:\:\:\:\: \\ $$$$ \\ $$

Question Number 188535 Answers: 1 Comments: 0

Question Number 188534 Answers: 1 Comments: 0

Question Number 188343 Answers: 1 Comments: 0

Find: Ω = Σ_(n=1) ^∞ (lim_(x→0) (1 - ((5 - (√(25 - x^2 )))/x) )^((5n)/x) )

$$\mathrm{Find}:\:\Omega\:=\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}\:-\:\frac{\mathrm{5}\:-\:\sqrt{\mathrm{25}\:-\:\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}}\:\right)^{\frac{\mathrm{5}\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{x}}}} \:\right) \\ $$

Question Number 188339 Answers: 1 Comments: 0

Question Number 188336 Answers: 1 Comments: 0

Pg 332 Pg 333 Pg 334 Pg 335 Pg 336 Pg 337 Pg 338 Pg 339 Pg 340 Pg 341

Contact: [email protected]