
AllQuestion and Answers: Page 336
Question Number 188557 Answers: 1 Comments: 0
$$\int\sqrt{\boldsymbol{{x}}\sqrt{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}}\boldsymbol{{dx}} \\ $$
Question Number 188552 Answers: 0 Comments: 1

Question Number 188549 Answers: 0 Comments: 3
Question Number 188545 Answers: 1 Comments: 0

Question Number 188544 Answers: 1 Comments: 0

Question Number 188543 Answers: 0 Comments: 0

Question Number 188521 Answers: 1 Comments: 2

Question Number 188520 Answers: 1 Comments: 0
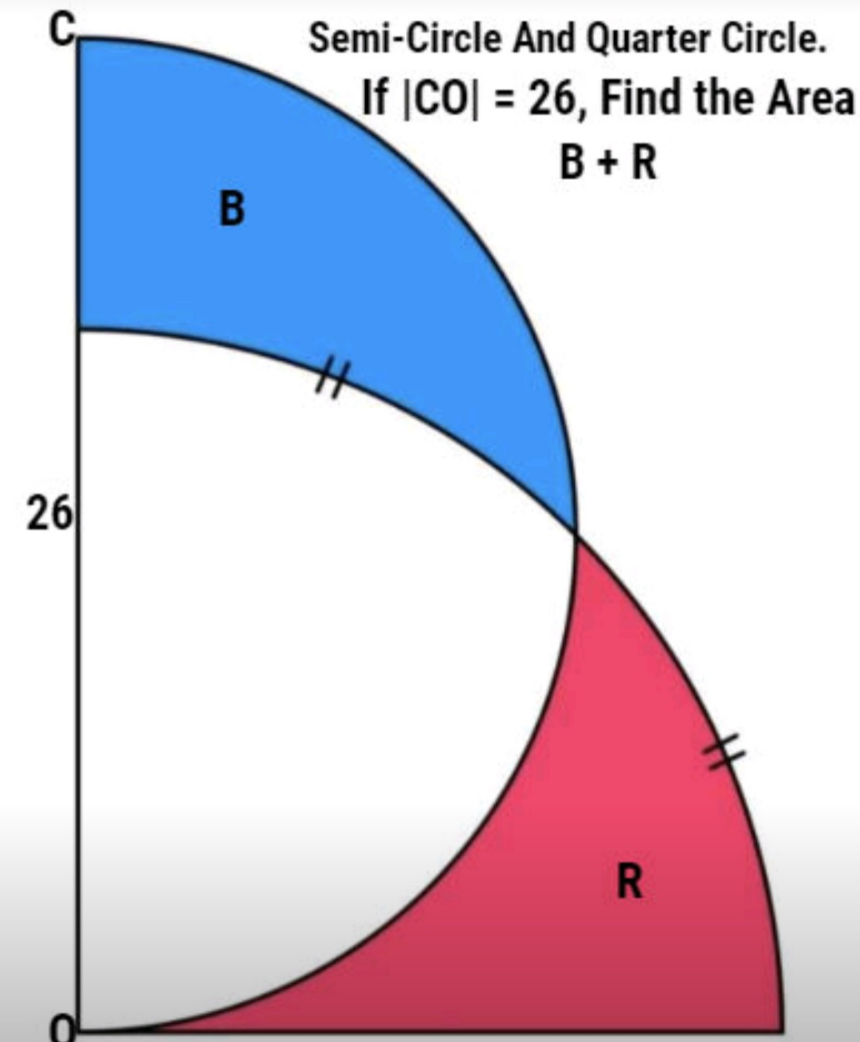
Question Number 188515 Answers: 1 Comments: 0
Question Number 188512 Answers: 0 Comments: 0
Question Number 188511 Answers: 0 Comments: 0
Question Number 188508 Answers: 2 Comments: 0

Question Number 188507 Answers: 0 Comments: 0
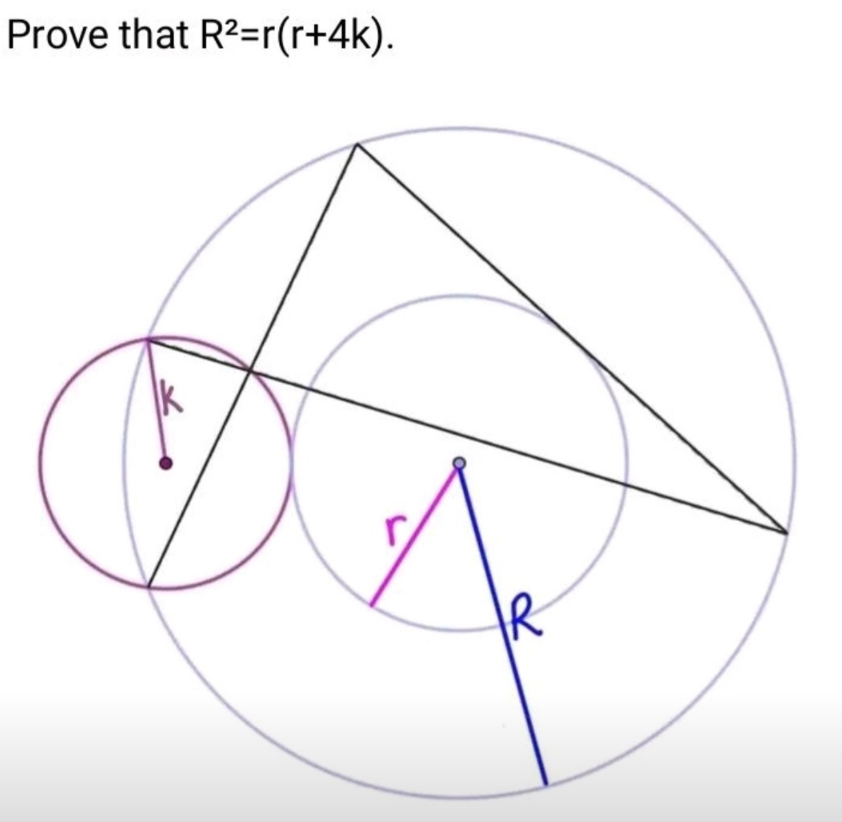
Question Number 188551 Answers: 1 Comments: 0
Question Number 188493 Answers: 0 Comments: 0

Question Number 188492 Answers: 2 Comments: 2

Question Number 188482 Answers: 1 Comments: 0
Question Number 188475 Answers: 1 Comments: 0
Question Number 188470 Answers: 0 Comments: 0
Question Number 188456 Answers: 0 Comments: 0

Question Number 188455 Answers: 1 Comments: 0
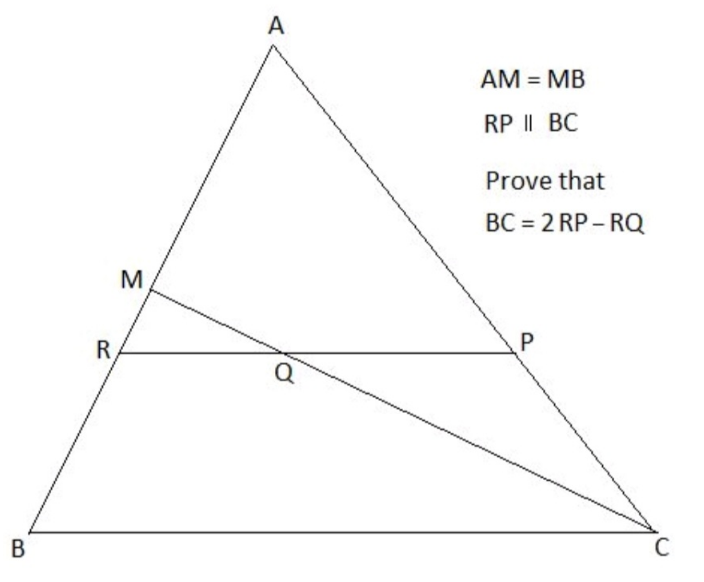
Question Number 188451 Answers: 3 Comments: 0

Question Number 188449 Answers: 1 Comments: 0
Question Number 188444 Answers: 1 Comments: 0

Question Number 188443 Answers: 1 Comments: 0
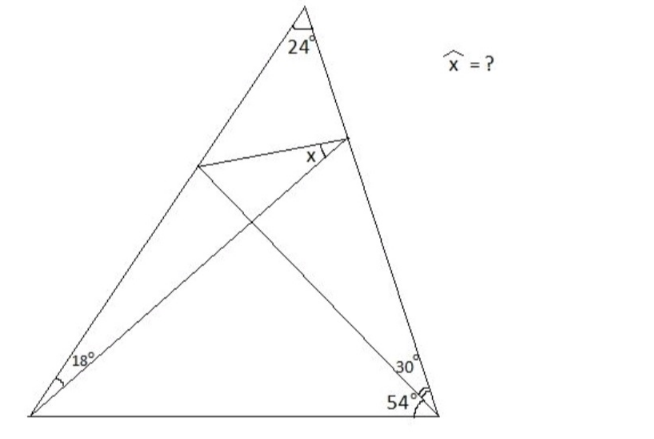
Question Number 188441 Answers: 1 Comments: 0

Pg 331 Pg 332 Pg 333 Pg 334 Pg 335 Pg 336 Pg 337 Pg 338 Pg 339 Pg 340
