Question and Answers Forum

AllQuestion and Answers: Page 332

Question Number 187270 Answers: 3 Comments: 0

lim_(x→π) ((cos x + sin(2x) +1)/(x^2 −π^2 )) = A. (1/(2π)) C. 1 B. (1/π) D. Does Not exist

$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{\mathrm{cos}\:{x}\:+\:\mathrm{sin}\left(\mathrm{2}{x}\right)\:+\mathrm{1}}{{x}^{\mathrm{2}} −\pi^{\mathrm{2}} }\:= \\ $$$$\mathrm{A}.\:\frac{\mathrm{1}}{\mathrm{2}\pi}\:\:\:\:\:\:\:\:\:{C}.\:\mathrm{1} \\ $$$${B}.\:\frac{\mathrm{1}}{\pi}\:\:\:\:\:\:\:\:\:{D}.\:\mathrm{Does}\:\mathrm{Not}\:\mathrm{exist} \\ $$

Question Number 187257 Answers: 0 Comments: 2

Question Number 187255 Answers: 1 Comments: 0

Find the directional derivatives of the function f(x,y,z)=2x^2 +3y^2 +z^2 at the point p(2,1,3)

$${Find}\:{the}\:{directional}\:{derivatives}\:{of}\:{the} \\ $$$${function}\: \\ $$$${f}\left({x},\mathrm{y},\mathrm{z}\right)=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:{at}\:{the}\:{point}\:{p}\left(\mathrm{2},\mathrm{1},\mathrm{3}\right) \\ $$

Question Number 187254 Answers: 1 Comments: 0

Question Number 187253 Answers: 4 Comments: 0

Question Number 187252 Answers: 1 Comments: 0

Question Number 187251 Answers: 0 Comments: 1

∫ ((cos 9x)/(cos 4x. cos 2x)) dx=?

$$\:\:\int\:\frac{\mathrm{cos}\:\mathrm{9}{x}}{\mathrm{cos}\:\mathrm{4}{x}.\:\mathrm{cos}\:\mathrm{2}{x}}\:{dx}=? \\ $$

Question Number 187248 Answers: 0 Comments: 1

what is the cardinality of the set of prime numbers whose base ten digits sums up to 10

$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{cardinality}\:\mathrm{of}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{prime}\:\mathrm{numbers}\:\mathrm{whose} \\ $$$$\mathrm{base}\:\mathrm{ten}\:\mathrm{digits}\:\mathrm{sums}\:\mathrm{up}\:\mathrm{to}\:\mathrm{10} \\ $$

Question Number 187235 Answers: 0 Comments: 4

Question Number 187233 Answers: 1 Comments: 1

Find x if : x^4 +a=x ∀ (0<a<(2/9))

$${Find}\:{x}\:{if}\::\:\:\:{x}^{\mathrm{4}} +{a}={x}\:\:\:\:\forall\:\left(\mathrm{0}<{a}<\frac{\mathrm{2}}{\mathrm{9}}\right)\:\:\: \\ $$

Question Number 187227 Answers: 0 Comments: 0

Question Number 187223 Answers: 0 Comments: 0

Question Number 187274 Answers: 0 Comments: 1

Question Number 187216 Answers: 1 Comments: 1

Question Number 187215 Answers: 1 Comments: 0

((√(n!))/n)=(√(20)) ; n=?

$$\frac{\sqrt{{n}!}}{{n}}=\sqrt{\mathrm{20}}\:;\:{n}=? \\ $$

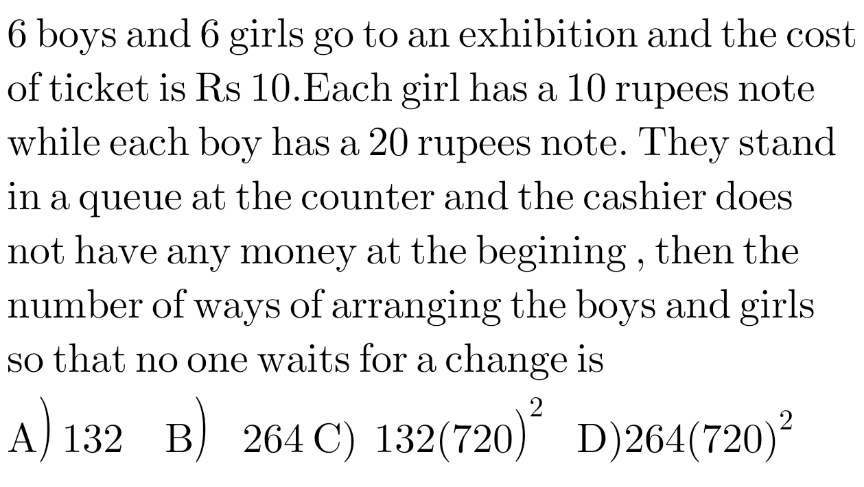
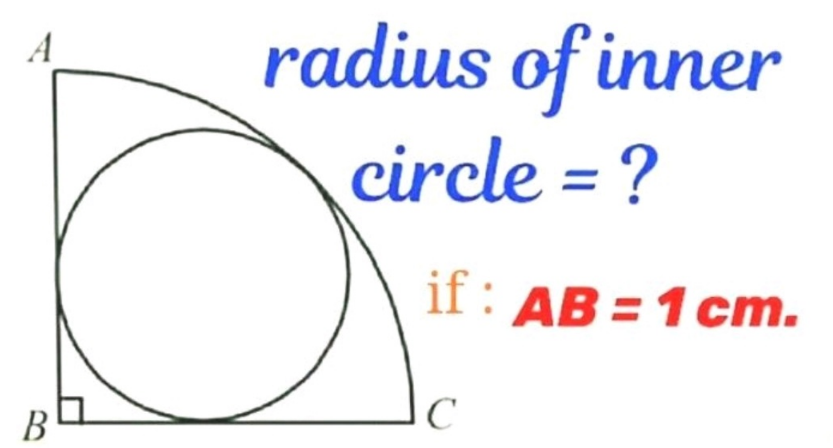
Question Number 187205 Answers: 3 Comments: 0

if the sides of a triangle are (√(a^2 +b^2 )), (√(a^2 +4b^2 )), (√(4a^2 +b^2 )) respectively, what is its area?

$${if}\:{the}\:{sides}\:{of}\:{a}\:{triangle}\:{are} \\ $$$$\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} },\:\sqrt{{a}^{\mathrm{2}} +\mathrm{4}{b}^{\mathrm{2}} },\:\sqrt{\mathrm{4}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:{respectively}, \\ $$$${what}\:{is}\:{its}\:{area}? \\ $$

Question Number 187213 Answers: 0 Comments: 0

If a,b are co-prime natural numbers satisfying a^2 + b = (a−b)^3 and b+1 is a prime find all possible values of (a, b). Please help me solve this.

$$\mathrm{If}\:{a},{b}\:\mathrm{are}\:\mathrm{co}-\mathrm{prime}\:\mathrm{natural}\:\mathrm{numbers}\:\mathrm{satisfying} \\ $$$${a}^{\mathrm{2}} \:+\:{b}\:=\:\left({a}−{b}\right)^{\mathrm{3}} \:\mathrm{and}\:{b}+\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{prime}\:\mathrm{find}\:\mathrm{all} \\ $$$$\mathrm{possible}\:\mathrm{values}\:\mathrm{of}\:\left({a},\:{b}\right). \\ $$$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{solve}\:\mathrm{this}. \\ $$$$ \\ $$

Question Number 187209 Answers: 0 Comments: 1

Question Number 187191 Answers: 2 Comments: 2

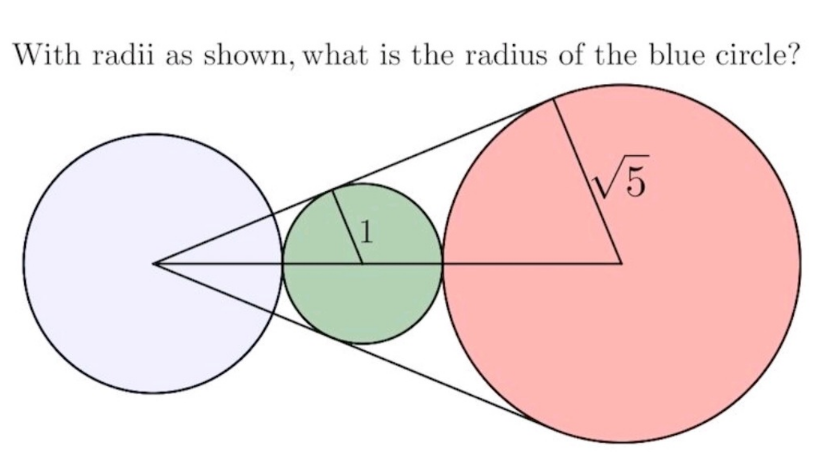
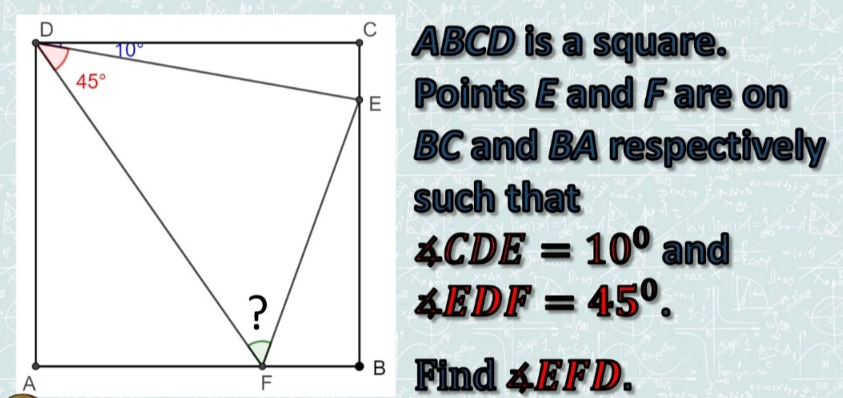
Question Number 187190 Answers: 2 Comments: 0

Question Number 187186 Answers: 2 Comments: 6

Question Number 187184 Answers: 0 Comments: 0

×/ { { {{×=

$$ ×/ \left\{ \left\{ \left\{\left\{×=\right.\right.\right.\right. \\ $$

Question Number 187177 Answers: 1 Comments: 0

2^y y^2 +(2y)^((2y)) =272

$$ \\ $$$$\mathrm{2}^{{y}} {y}^{\mathrm{2}} +\left(\mathrm{2}{y}\right)^{\left(\mathrm{2}{y}\right)} =\mathrm{272} \\ $$

Question Number 187176 Answers: 1 Comments: 0

Question Number 187168 Answers: 0 Comments: 0

Question Number 187167 Answers: 3 Comments: 0

Pg 327 Pg 328 Pg 329 Pg 330 Pg 331 Pg 332 Pg 333 Pg 334 Pg 335 Pg 336

Contact: info@tinkutara.com