Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 325

Question Number 189523 Answers: 0 Comments: 0

Question Number 189522 Answers: 0 Comments: 2

Question Number 189521 Answers: 0 Comments: 0

Question Number 189517 Answers: 1 Comments: 1

Question Number 189514 Answers: 0 Comments: 0

Question Number 189509 Answers: 1 Comments: 0

Question Number 189507 Answers: 0 Comments: 0

Question Number 189506 Answers: 1 Comments: 0

Question Number 189496 Answers: 2 Comments: 0

∫ xe^(x^2 /2) dx

$$\int\:\mathrm{xe}^{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\mathrm{dx} \\ $$

Question Number 189495 Answers: 0 Comments: 7

Question Number 189489 Answers: 1 Comments: 1

Ω= ∫_0 ^( ∞) e^( −x) cos(x)ln(x)dx=? −−− f (a )= ∫_0 ^( ∞) e^( −x) cos(x)x^( a) dx = Re ∫_0 ^( ∞) e^( −x) .e^( −ix) .x^( a) dx = Re ∫_0 ^( ∞) e^( −x (1+i)) .x^( a) dx = Re(L { x^( a) }∣_( s= i+1) ) = Re( ((Γ (1+a))/s^( a+1) ) ∣_( 1+i) = ((Γ (1+a))/((1+i)^( a+1) )) ) Re (Γ(1+a).2^( ((1+a)/2)) . e^( −((iπ)/4) (1+a)) ) Ω= f ′(0)=.......

$$ \\ $$$$\:\:\:\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\infty} {e}^{\:−{x}} {cos}\left({x}\right){ln}\left({x}\right){dx}=? \\ $$$$\:\:\:\:\:−−− \\ $$$$\:\:\:\:\:\:{f}\:\left({a}\:\right)=\:\int_{\mathrm{0}} ^{\:\infty} {e}^{\:−{x}} {cos}\left({x}\right){x}^{\:{a}} \:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{Re}\:\int_{\mathrm{0}} ^{\:\infty} {e}^{\:−{x}} .{e}^{\:−{ix}} .{x}^{\:{a}} {dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:{Re}\:\int_{\mathrm{0}} ^{\:\infty} \:{e}^{\:−{x}\:\left(\mathrm{1}+{i}\right)} .{x}^{\:{a}} \:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:{Re}\left(\mathscr{L}\:\:\left\{\:{x}^{\:{a}} \:\right\}\mid_{\:{s}=\:{i}+\mathrm{1}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:=\:{Re}\left(\:\frac{\Gamma\:\left(\mathrm{1}+{a}\right)}{{s}^{\:{a}+\mathrm{1}} }\:\mid_{\:\mathrm{1}+{i}} =\:\frac{\Gamma\:\left(\mathrm{1}+{a}\right)}{\left(\mathrm{1}+{i}\right)^{\:{a}+\mathrm{1}} }\:\right) \\ $$$$\:\:\:\:\:\:\:\:{Re}\:\left(\Gamma\left(\mathrm{1}+{a}\right).\mathrm{2}^{\:\frac{\mathrm{1}+{a}}{\mathrm{2}}} .\:{e}^{\:−\frac{{i}\pi}{\mathrm{4}}\:\left(\mathrm{1}+{a}\right)} \right) \\ $$$$\:\:\:\:\Omega=\:{f}\:'\left(\mathrm{0}\right)=....... \\ $$$$\:\: \\ $$

Question Number 189484 Answers: 1 Comments: 1

Question Number 189501 Answers: 3 Comments: 0

lim_(x→0) ((e^(x+2x+3x+4x+.....+nx) −1)/x)=?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}+\mathrm{2}{x}+\mathrm{3}{x}+\mathrm{4}{x}+.....+{nx}} −\mathrm{1}}{{x}}=? \\ $$

Question Number 189482 Answers: 2 Comments: 0

If tan 11° = x then tan 1° = ?

$$\mathrm{If}\:\mathrm{tan}\:\mathrm{11}°\:=\:{x}\:\mathrm{then}\:\mathrm{tan}\:\mathrm{1}°\:=\:?\: \\ $$

Question Number 189473 Answers: 1 Comments: 0

Question Number 189461 Answers: 0 Comments: 0

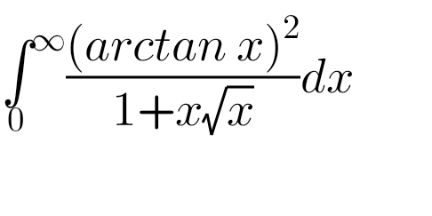
Question Number 189455 Answers: 0 Comments: 0

Question Number 189449 Answers: 1 Comments: 0

Question Number 189446 Answers: 1 Comments: 0

x^2 =(2)^(1/5) +y y^2 =(2)^(1/5) +x x∙y=? x≠y

$${x}^{\mathrm{2}} =\sqrt[{\mathrm{5}}]{\mathrm{2}}+{y} \\ $$$${y}^{\mathrm{2}} =\sqrt[{\mathrm{5}}]{\mathrm{2}}+{x} \\ $$$${x}\centerdot{y}=?\:\:\:\:\:\:\:\:\:\:\:{x}\neq{y} \\ $$

Question Number 189445 Answers: 2 Comments: 0

Question Number 189429 Answers: 1 Comments: 1

Question Number 189428 Answers: 1 Comments: 0

Question Number 189426 Answers: 0 Comments: 0

Question Number 189421 Answers: 1 Comments: 1

Question Number 189418 Answers: 1 Comments: 0

Know: f(x)=3x+2+∫^1 _0 xf(x)dx Eluavte: ∫^2 _0 f(x)dx=¿

$${Know}:\:{f}\left({x}\right)=\mathrm{3}{x}+\mathrm{2}+\underset{\mathrm{0}} {\int}^{\mathrm{1}} {xf}\left({x}\right){dx} \\ $$$${Eluavte}:\:\underset{\mathrm{0}} {\int}^{\mathrm{2}} {f}\left({x}\right){dx}=¿ \\ $$

Question Number 189417 Answers: 1 Comments: 0

Pg 320 Pg 321 Pg 322 Pg 323 Pg 324 Pg 325 Pg 326 Pg 327 Pg 328 Pg 329

Terms of Service

Contact: info@tinkutara.com