Question and Answers Forum

AllQuestion and Answers: Page 322

Question Number 190038 Answers: 1 Comments: 0

Find: ((21 + (√(4a − 3)))/(4a + (√(3 − 4a))))

$$\mathrm{Find}:\:\:\:\frac{\mathrm{21}\:+\:\sqrt{\mathrm{4a}\:−\:\mathrm{3}}}{\mathrm{4a}\:+\:\sqrt{\mathrm{3}\:−\:\mathrm{4a}}} \\ $$

Question Number 190035 Answers: 1 Comments: 0

10^(93) − 93 Find the sum of the numbers

$$\mathrm{10}^{\mathrm{93}} \:−\:\mathrm{93} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{numbers} \\ $$

Question Number 190034 Answers: 3 Comments: 0

If x + (2/x) = (√(17)) Find: (((x^2 − 4)(x^2 − 1))/x^2 ) = ?

$$\mathrm{If}\:\:\:\mathrm{x}\:+\:\frac{\mathrm{2}}{\mathrm{x}}\:=\:\sqrt{\mathrm{17}} \\ $$$$\mathrm{Find}:\:\:\:\frac{\left(\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{4}\right)\left(\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} }\:=\:? \\ $$

Question Number 190032 Answers: 4 Comments: 0

x > 0 xy − 18 = 0 (2x + y)_(min) = ?

$$\mathrm{x}\:>\:\mathrm{0} \\ $$$$\mathrm{xy}\:−\:\mathrm{18}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2x}\:+\:\mathrm{y}\right)_{\boldsymbol{\mathrm{min}}} \:=\:? \\ $$

Question Number 190027 Answers: 1 Comments: 0

a^2 + b^2 = 12 ab = 4 Fund: a^3 + b^3 = ?

$$\mathrm{a}^{\mathrm{2}} \:+\:\mathrm{b}^{\mathrm{2}} \:=\:\mathrm{12} \\ $$$$\mathrm{ab}\:=\:\mathrm{4} \\ $$$$\mathrm{Fund}:\:\:\:\mathrm{a}^{\mathrm{3}} \:+\:\mathrm{b}^{\mathrm{3}} \:=\:? \\ $$

Question Number 190025 Answers: 1 Comments: 0

If f(x) = 3x^5 + 2x^2 Find: f((√2) − 1) + f(1 − (√2)) + 3

$$\mathrm{If}\:\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{3x}^{\mathrm{5}} \:+\:\mathrm{2x}^{\mathrm{2}} \\ $$$$\mathrm{Find}:\:\:\:\mathrm{f}\left(\sqrt{\mathrm{2}}\:−\:\mathrm{1}\right)\:+\:\mathrm{f}\left(\mathrm{1}\:−\:\sqrt{\mathrm{2}}\right)\:+\:\mathrm{3} \\ $$

Question Number 190024 Answers: 1 Comments: 0

Find: (√(4+(√2))) ∙ (√(3+(√(5+(√2))))) ∙ (√(3−(√(5+(√2))))) + ∣(√(14))−4∣

$$\mathrm{Find}: \\ $$$$\sqrt{\mathrm{4}+\sqrt{\mathrm{2}}}\:\centerdot\:\sqrt{\mathrm{3}+\sqrt{\mathrm{5}+\sqrt{\mathrm{2}}}}\:\centerdot\:\sqrt{\mathrm{3}−\sqrt{\mathrm{5}+\sqrt{\mathrm{2}}}}\:+\:\mid\sqrt{\mathrm{14}}−\mathrm{4}\mid \\ $$

Question Number 190022 Answers: 1 Comments: 2

5x^2 − 3x + 5 = 0 Find: x + (1/x) = 0

$$\mathrm{5x}^{\mathrm{2}} \:−\:\mathrm{3x}\:+\:\mathrm{5}\:=\:\mathrm{0} \\ $$$$\mathrm{Find}:\:\:\:\mathrm{x}\:+\:\frac{\mathrm{1}}{\mathrm{x}}\:=\:\mathrm{0} \\ $$

Question Number 190017 Answers: 0 Comments: 0

Question Number 190009 Answers: 0 Comments: 2

Question Number 190006 Answers: 0 Comments: 0

Question Number 190005 Answers: 0 Comments: 0

Question Number 189998 Answers: 2 Comments: 0

tanA=(1/(n+1)) tanB=(n/(2n+1)) ⇒ A+B=?

$$\mathrm{tanA}=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{tanB}=\frac{\mathrm{n}}{\mathrm{2n}+\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{A}+\mathrm{B}=?\: \\ $$

Question Number 189989 Answers: 1 Comments: 0

Question Number 189986 Answers: 1 Comments: 0

Question Number 189984 Answers: 0 Comments: 0

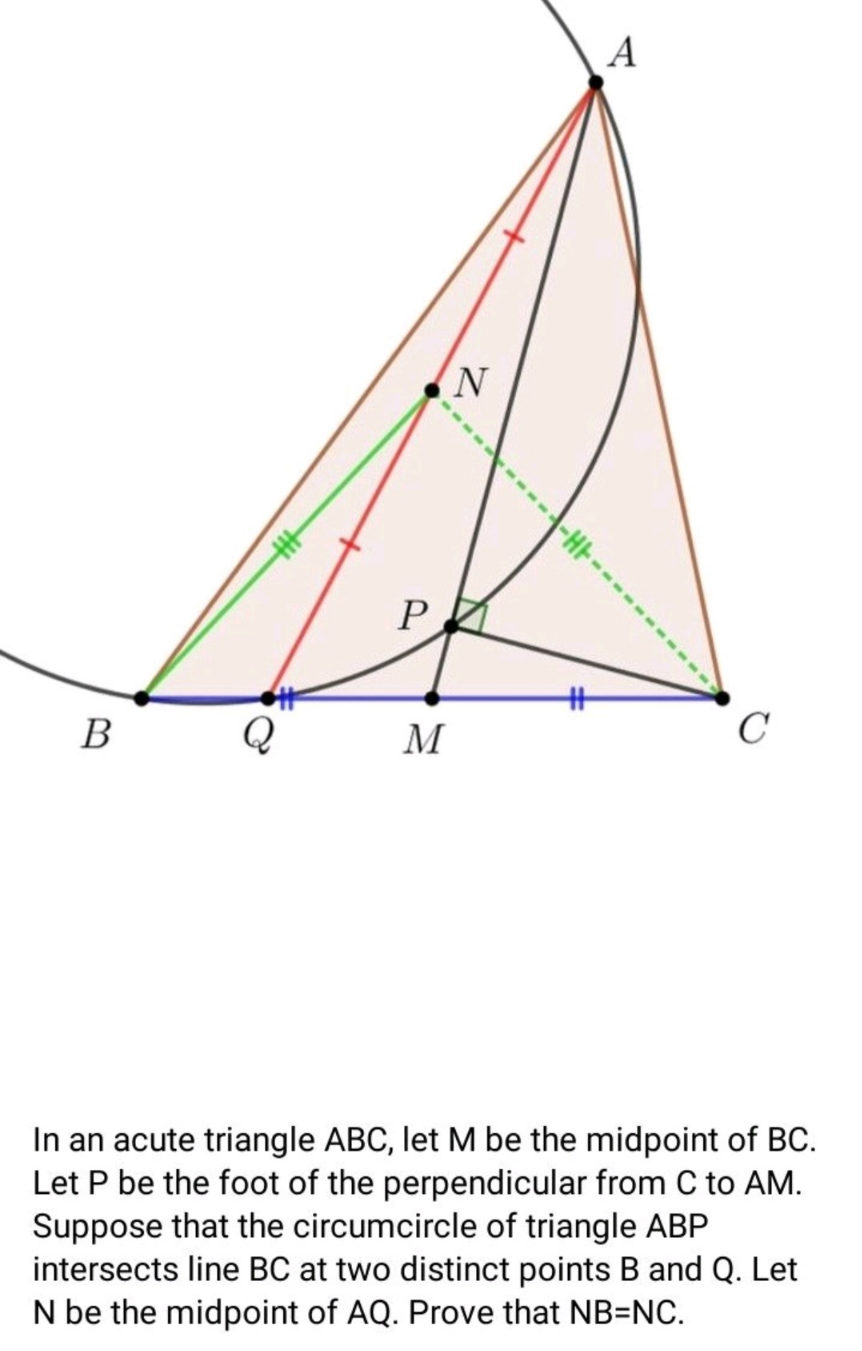
Question Number 189980 Answers: 1 Comments: 0

Question Number 189977 Answers: 1 Comments: 0

Question Number 189976 Answers: 2 Comments: 0

Question Number 189975 Answers: 1 Comments: 0

Question Number 189973 Answers: 3 Comments: 4

Question Number 189971 Answers: 1 Comments: 0

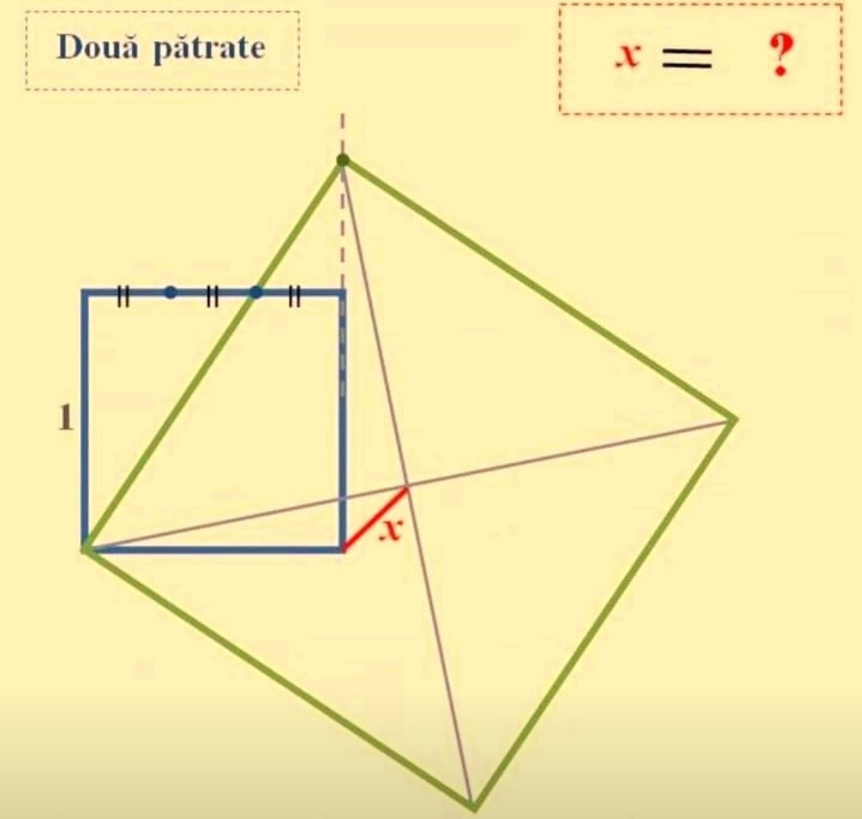
Question Number 189970 Answers: 1 Comments: 0

Question Number 189965 Answers: 3 Comments: 0

Question Number 190021 Answers: 0 Comments: 0

Find: lim_(n→∞) H_n (Σ_(k=1) ^n (1/(n+k)) -Σ_(k=1) ^n cot^(-1) (n+k))

$$\mathrm{Find}: \\ $$$$\underset{\boldsymbol{\mathrm{n}}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{H}_{\boldsymbol{\mathrm{n}}} \:\left(\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\boldsymbol{\mathrm{n}}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}\:-\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\boldsymbol{\mathrm{n}}} {\sum}}\:\mathrm{cot}^{-\mathrm{1}} \:\left(\mathrm{n}+\mathrm{k}\right)\right) \\ $$

Question Number 190019 Answers: 1 Comments: 3

Pg 317 Pg 318 Pg 319 Pg 320 Pg 321 Pg 322 Pg 323 Pg 324 Pg 325 Pg 326

Contact: [email protected]