Question and Answers Forum

AllQuestion and Answers: Page 316

Question Number 187076 Answers: 3 Comments: 0

(a/b)+(b/a)=5 ; (a^2 /b)+(b^2 /a) =12 (1/a)+(1/b)=?

$$\frac{{a}}{{b}}+\frac{{b}}{{a}}=\mathrm{5}\:\:;\:\frac{{a}^{\mathrm{2}} }{{b}}+\frac{{b}^{\mathrm{2}} }{{a}}\:=\mathrm{12} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=? \\ $$

Question Number 187073 Answers: 0 Comments: 0

suppose that a sample of size n=8 is drawn from a population with PDF: {f(x)=(x^2 /9), 0 < x < 3} find (1) p(1 < x < 2) (2) PDF and CDF of the fourth smallest O.S

$${suppose}\:{that}\:{a}\:{sample}\:{of}\:{size} \\ $$$${n}=\mathrm{8}\:{is}\:{drawn}\:{from}\:{a}\:{population}\:{with}\:{PDF}:\: \\ $$$$\left\{{f}\left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{9}},\:\mathrm{0}\:<\:{x}\:<\:\mathrm{3}\right\} \\ $$$${find} \\ $$$$\left(\mathrm{1}\right)\:\:\:{p}\left(\mathrm{1}\:<\:{x}\:<\:\mathrm{2}\right) \\ $$$$\left(\mathrm{2}\right)\:\:{PDF}\:{and}\:{CDF}\:{of}\:{the}\:{fourth}\:{smallest}\:{O}.{S} \\ $$

Question Number 187072 Answers: 0 Comments: 0

let x be the Discrete random variable with (PGF) P_x (t) = (t/5)(2+3t^2 ) find the distribution of x

$${let}\:{x}\:{be}\:{the}\:{Discrete}\:{random}\:{variable}\:{with}\:\left({PGF}\right)\: \\ $$$${P}_{{x}} \left({t}\right)\:=\:\frac{{t}}{\mathrm{5}}\left(\mathrm{2}+\mathrm{3}{t}^{\mathrm{2}} \right) \\ $$$${find}\:{the}\:{distribution}\:{of}\:{x} \\ $$

Question Number 187069 Answers: 1 Comments: 0

(2x −3y +2z +4)^(2 ) +(x−y−z)^2 +(x+y+z−8)^2 =0 find x , y, z

$$\left(\mathrm{2}{x}\:−\mathrm{3}{y}\:+\mathrm{2}{z}\:+\mathrm{4}\right)^{\mathrm{2}\:} +\left({x}−{y}−{z}\right)^{\mathrm{2}} +\left({x}+{y}+{z}−\mathrm{8}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${find} \\ $$$${x}\:,\:{y},\:{z}\: \\ $$

Question Number 187066 Answers: 3 Comments: 1

Question Number 187059 Answers: 1 Comments: 1

Question Number 187054 Answers: 0 Comments: 2

Question Number 187053 Answers: 1 Comments: 0

How do you make a curve y=ax^3 +bx^2 +cx+d with a critical point of (1,0) and (−2,27) ?

$$\:{How}\:{do}\:{you}\:{make}\:{a}\:{curve}\: \\ $$$$\:{y}={ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}\:{with}\:{a}\:{critical} \\ $$$$\:{point}\:{of}\:\left(\mathrm{1},\mathrm{0}\right)\:{and}\:\left(−\mathrm{2},\mathrm{27}\right)\:? \\ $$

Question Number 187051 Answers: 0 Comments: 1

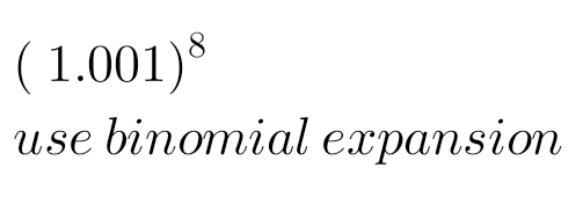
Question Number 187050 Answers: 0 Comments: 1

∫^(𝛑/4) _0 ((cos^(−1) x + cos x)/(Ln x)) dx =??

$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\underset{\mathrm{0}} {\int}^{\frac{\boldsymbol{\pi}}{\mathrm{4}}} \:\:\frac{\boldsymbol{{cos}}^{−\mathrm{1}} \boldsymbol{{x}}\:+\:\boldsymbol{{cos}}\:\boldsymbol{{x}}}{\boldsymbol{{Ln}}\:\boldsymbol{{x}}}\:\:\boldsymbol{{dx}}\:=??\:\:\: \\ $$$$ \\ $$

Question Number 187046 Answers: 1 Comments: 0

find the general solution for the following system of equations ((dx_1 /dt))=2x_1 +2x_2 ((dx_2 /dt))=x_1 +3x_2

$${find}\:\:\:{the}\:{general}\:\:{solution}\:{for}\:\:{the}\:{following} \\ $$$${system}\:{of}\:{equations} \\ $$$$\left(\frac{{dx}_{\mathrm{1}} }{{dt}}\right)=\mathrm{2}{x}_{\mathrm{1}} +\mathrm{2}{x}_{\mathrm{2}} \\ $$$$\left(\frac{{dx}_{\mathrm{2}} }{{dt}}\right)={x}_{\mathrm{1}} +\mathrm{3}{x}_{\mathrm{2}} \\ $$$$ \\ $$

Question Number 187029 Answers: 1 Comments: 0

Question Number 187027 Answers: 1 Comments: 0

Question Number 187025 Answers: 1 Comments: 0

Question Number 187044 Answers: 0 Comments: 0

f(x,y)={(x+y),0<x<1, 0<y<1 0, otherwise find: (1) σxy (2) p(0<x<((1/4))∣((2/5))>y>((1/3))) note: f(x,y) is the joint PDF

$${f}\left({x},{y}\right)=\left\{\left({x}+{y}\right),\mathrm{0}<{x}<\mathrm{1},\:\mathrm{0}<{y}<\mathrm{1}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0},\:{otherwise} \\ $$$${find}: \\ $$$$\left(\mathrm{1}\right)\:\sigma{xy} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\:{p}\left(\mathrm{0}<{x}<\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\mid\left(\frac{\mathrm{2}}{\mathrm{5}}\right)>{y}>\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right) \\ $$$$ \\ $$$${note}:\:{f}\left({x},{y}\right)\:{is}\:{the}\:{joint}\:{PDF} \\ $$

Question Number 187020 Answers: 0 Comments: 1

(a/x)=(b/y)=(c/z)=(1/3) ,a−2b+c=2 and 2y−3z=1 x=? how is solution

$$\frac{{a}}{{x}}=\frac{{b}}{{y}}=\frac{{c}}{{z}}=\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:,{a}−\mathrm{2}{b}+{c}=\mathrm{2}\:\:{and}\:\:\mathrm{2}{y}−\mathrm{3}{z}=\mathrm{1}\:\:\:\:{x}=? \\ $$$${how}\:{is}\:{solution} \\ $$

Question Number 187011 Answers: 0 Comments: 0

a∈C determinant (((a 1 … 1)),((1 ⋱ ⋱ ⋮)),((⋮ ⋱ ⋱ 1)),((1 … 1 a)))=?

$$\mathrm{a}\in\mathbb{C} \\ $$$$\begin{vmatrix}{\mathrm{a}\:\:\:\mathrm{1}\:\:\:\:\ldots\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\ddots\:\:\ddots\:\:\vdots}\\{\vdots\:\:\ddots\:\:\ddots\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\ldots\:\:\:\:\mathrm{1}\:\:\:\mathrm{a}}\end{vmatrix}=? \\ $$

Question Number 187010 Answers: 0 Comments: 0

a,b∈C determinant (((a+b a 0 … 0)),(( b a+b ⋱ ⋱ ⋮)),(( 0 ⋱ ⋱ ⋱ 0)),(( ⋮ ⋱ ⋱ ⋱ a)),(( 0 … 0 b a+b)))=?

Question Number 187008 Answers: 2 Comments: 0

(a/3)=(b/4)=(c/5) 3a+c=42 b=? how is solution

$$\frac{{a}}{\mathrm{3}}=\frac{{b}}{\mathrm{4}}=\frac{{c}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}{a}+{c}=\mathrm{42}\:\:\:\:\:\:\:\:{b}=? \\ $$$${how}\:{is}\:{solution} \\ $$

Question Number 187007 Answers: 0 Comments: 2

prove that 7^(k+1) ∣ 13^(7k) + 1 , ∀k∈N

$${prove}\:\:{that} \\ $$$$\mathrm{7}^{{k}+\mathrm{1}} \mid\:\mathrm{13}^{\mathrm{7}{k}} \:+\:\mathrm{1}\:,\:\forall{k}\in\mathbb{N} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Question Number 186999 Answers: 0 Comments: 0

Question Number 186998 Answers: 1 Comments: 1

Question Number 186996 Answers: 1 Comments: 0

Question Number 186989 Answers: 0 Comments: 0

Question Number 186983 Answers: 3 Comments: 0

Question Number 186960 Answers: 1 Comments: 0

Pg 311 Pg 312 Pg 313 Pg 314 Pg 315 Pg 316 Pg 317 Pg 318 Pg 319 Pg 320

Contact: info@tinkutara.com